
Reflection (mathematics)
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a reflection (also spelled reflexion) is a mapping
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
from a Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
to itself that is an isometry
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
with a hyperplane
Hyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
as set of fixed point
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
s; this set is called the axis (in dimension 2) or plane
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
(in dimension 3) of reflection. The image of a figure by a reflection is its mirror image
Mirror image
A mirror image is a reflected duplication of an object that appears identical but reversed. As an optical effect it results from reflection off of substances such as a mirror or water. It is also a concept in geometry and can be used as a conceptualization process for 3-D structures...
in the axis or plane of reflection. For example the mirror image of the small Latin letter p for a reflection with respect to a vertical axis would look like q. Its image by reflection in a horizontal axis would look like b. A reflection is an involution: when applied twice in succession, every point returns to its original location, and every geometrical object is restored to its original state.
The term "reflection" is sometimes used for a larger class of mappings from a Euclidean space to itself, namely the non-identity isometries that are involutions. Such isometries have a set of fixed points (the "mirror") that is an affine subspace, but is possibly smaller than a hyperplane. For instance a reflection through a point
Point reflection
In geometry, a point reflection or inversion in a point is a type of isometry of Euclidean space...
is an involutive isometry with just one fixed point; the image of the letter p under it
would look like a d. This operation is also known as a central inversion
Point reflection
In geometry, a point reflection or inversion in a point is a type of isometry of Euclidean space...
, and exhibits Euclidean space as a symmetric space
Symmetric space
A symmetric space is, in differential geometry and representation theory, a smooth manifold whose group of symmetries contains an "inversion symmetry" about every point...
. In a Euclidean vector space, the reflection in the point situated at the origin is the same as vector negation. Other examples include reflections in a line in three dimensional space. Typically, however, unqualified use of the term "reflection" means reflection in a hyperplane
Hyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
.
A figure which does not change upon undergoing a reflection is said to have reflectional symmetry
Reflection symmetry
Reflection symmetry, reflectional symmetry, line symmetry, mirror symmetry, mirror-image symmetry, or bilateral symmetry is symmetry with respect to reflection. That is, a figure which does not change upon undergoing a reflection has reflectional symmetry.In 2D there is a line of symmetry, in 3D a...
.
Construction
In plane (or 3-dimensional) geometry, to find the reflection of a point one drops a perpendicularPerpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
from the point onto the line (plane) used for reflection, and continues it to the same distance on the other side. To find the reflection of a figure, one reflects each point in the figure.
Properties
The matrixMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
for a reflection is orthogonal
Orthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
with determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
-1 and eigenvalues (1, 1, 1, ... 1, -1). The product of two such matrices is a special orthogonal matrix which represents a rotation. Every rotation
Rotation (mathematics)
In geometry and linear algebra, a rotation is a transformation in a plane or in space that describes the motion of a rigid body around a fixed point. A rotation is different from a translation, which has no fixed points, and from a reflection, which "flips" the bodies it is transforming...
is the result of reflecting in an even number of reflections in hyperplanes through the origin, and every improper rotation
Improper rotation
In 3D geometry, an improper rotation, also called rotoreflection or rotary reflection is, depending on context, a linear transformation or affine transformation which is the combination of a rotation about an axis and a reflection in a plane perpendicular to the axis.Equivalently it is the...
is the result of reflecting in an odd number. Thus reflections generate the orthogonal group
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
, and this result is known as the Cartan–Dieudonné theorem.
Similarly the Euclidean group
Euclidean group
In mathematics, the Euclidean group E, sometimes called ISO or similar, is the symmetry group of n-dimensional Euclidean space...
, which consists of all isometries of Euclidean space, is generated by reflections in affine hyperplanes. In general, a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
generated by reflections in affine hyperplanes is known as a reflection group
Reflection group
In group theory and geometry, a reflection group is a discrete group which is generated by a set of reflections of a finite-dimensional Euclidean space. The symmetry group of a regular polytope or of a tiling of the Euclidean space by congruent copies of a regular polytope is necessarily a...
. The finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
s generated in this way are examples of Coxeter group
Coxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
s.
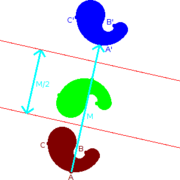
Reflection across a line in the plane
Reflection across a line through the origin in two dimensions can be described by the following formula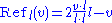
Where v denotes the vector being reflected, l denotes the line being reflected in, and v·l denotes the dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
of v with l. Note the formula above can also be described as
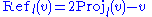
Where the reflection of line l on a is equal to 2 times the projection of v on line l minus v.
Reflections in a line have the eigenvalues of 1, and −1.
Reflection through a hyperplane in n dimensions
Given a vector a in Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn, the formula for the reflection in the hyperplane
Hyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
through the origin, orthogonal to a, is given by

where v·a denotes the dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
of v with a. Note that the second term in the above equation is just twice the vector projection of v onto a. One can easily check that
- Refa(v) = − v, if v is parallel to a, and
- Refa(v) = v, if v is perpendicular to a.
Using the geometric product the formula is a little simpler
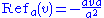
Since these reflections are isometries of Euclidean space fixing the origin, they may be represented by orthogonal matrices. The orthogonal matrix corresponding to the above reflection is the matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
whose entries are

where δij is the Kronecker delta.
The formula for the reflection in the affine hyperplane
 not through the origin is
not through the origin is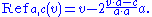
See also
- Coordinate rotations and reflectionsCoordinate rotations and reflectionsIn geometry, 2D coordinate rotations and reflections are two kinds of Euclidean plane isometries which are related to one another.A rotation in the plane can be formed by composing a pair of reflections. First reflect a point P to its image P′ on the other side of line L1...
- Householder transformationHouseholder transformationIn linear algebra, a Householder transformation is a linear transformation that describes a reflection about a plane or hyperplane containing the origin. Householder transformations are widely used in numerical linear algebra, to perform QR decompositions and in the first step of the QR algorithm...
- Inversive geometry
- Point reflectionPoint reflectionIn geometry, a point reflection or inversion in a point is a type of isometry of Euclidean space...
- Plane of rotationPlane of rotationIn geometry, a plane of rotation is an abstract object used to describe or visualise rotations in space. In three dimensions it is an alternative to the axis of rotation, but unlike the axis of rotation it can be used in other dimensions, such as two, four or more dimensions.Mathematically such...
- Reflection mappingReflection mappingIn computer graphics, environment mapping, or reflection mapping, is an efficient Image-based lighting technique for approximating the appearance of a reflective surface by means of a precomputed texture image. The texture is used to store the image of the distant environment surrounding the...
- Reflection groupReflection groupIn group theory and geometry, a reflection group is a discrete group which is generated by a set of reflections of a finite-dimensional Euclidean space. The symmetry group of a regular polytope or of a tiling of the Euclidean space by congruent copies of a regular polytope is necessarily a...
External links
- Reflection in Line at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- Understanding 2D Reflection and Understanding 3D Reflection by Roger Germundsson, The Wolfram Demonstrations Project.

