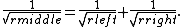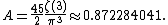Ford circle
Encyclopedia
In mathematics
, a Ford circle is a circle
with centre
at (p/q, 1/(2q 2)) and radius
1/(2q 2), where p/q is an irreducible fraction
, i.e. p and q are coprime
integers. Each Ford circle is tangent to the horizontal axis y = 0.
, after whom the problem of Apollonius
and the Apollonian gasket
are named. In the 17th century René Descartes
discovered Descartes' theorem
, a relationship between the reciprocals of the radii of mutually tangent circles.
Ford circles also appear in the Sangaku
(geometrical puzzles) of Japanese mathematics
. A typical problem, which is presented on an 1824 tablet in the Gunma Prefecture
, covers the relationship of three touching circles with a common tangent
. Given the size of the two outer large circles, what is the size of the small circle between then? The answer is equivalent to a Ford circle:
Ford circles are named after American mathematician Lester R. Ford, Sr., who described them in an article in American Mathematical Monthly
in 1938, volume 45, number 9, pages 586–601.
. In addition, the line y = 1 is counted as a Ford circle – it can be thought of as the Ford circle associated with infinity
, which is the case p = 1, q = 0.
Two different Ford circles are either disjoint or tangent
to one another. No two interiors of Ford circles intersect – even though there is a Ford circle tangent to the x-axis
at each point on it with rational
co-ordinates. If p/q is between 0 and 1, the Ford circles that are tangent to C[p/q] can be described variously as
Ford circles can also be thought of as curves in the complex plane
. The modular group of transformations of the complex plane maps Ford circles to other Ford circles.
By interpreting the upper half of the complex plane as a model of the hyperbolic plane
(the Poincaré half-plane model) Ford circles can also be interpreted as a tiling
of the hyperbolic plane by horocycle
s. Any two Ford circles are congruent
in hyperbolic geometry
. If C[p/q] and C[r/s] are tangent Ford circles, then the half-circle joining (p/q, 0) and (r/s, 0) that is perpendicular to the x-axis is a hyperbolic line that also passes through the point where the two circles are tangent to one another.
Ford circles are a sub-set of the circles in the Apollonian gasket
generated by the lines y = 0 and y = 1 and the circle C[0/1].
φ and the Riemann zeta function.
As no two Ford circles intersect, it follows immediately that the total area of the Ford circles
is less than 1. In fact the total area of these Ford circles is given by a convergent sum, which can be evaluated.
From the definition, the area is
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Ford circle is a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
with centre
Centre (geometry)
In geometry, the centre of an object is a point in some sense in the middle of the object. If geometry is regarded as the study of isometry groups then the centre is a fixed point of the isometries.-Circles:...
at (p/q, 1/(2q 2)) and radius
Radius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
1/(2q 2), where p/q is an irreducible fraction
Irreducible fraction
An irreducible fraction is a vulgar fraction in which the numerator and denominator are smaller than those in any other equivalent vulgar fraction...
, i.e. p and q are coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
integers. Each Ford circle is tangent to the horizontal axis y = 0.
History
Ford circles are a special case of mutually tangent circles; the base line can be thought of as a circle with infinite radius. Systems of mutually tangent circles were studied by Apollonius of PergaApollonius of Perga
Apollonius of Perga [Pergaeus] was a Greek geometer and astronomer noted for his writings on conic sections. His innovative methodology and terminology, especially in the field of conics, influenced many later scholars including Ptolemy, Francesco Maurolico, Isaac Newton, and René Descartes...
, after whom the problem of Apollonius
Problem of Apollonius
In Euclidean plane geometry, Apollonius' problem is to construct circles that are tangent to three given circles in a plane . Apollonius of Perga posed and solved this famous problem in his work ; this work has been lost, but a 4th-century report of his results by Pappus of Alexandria has survived...
and the Apollonian gasket
Apollonian gasket
In mathematics, an Apollonian gasket or Apollonian net is a fractal generated from triples of circles, where each circle is tangent to the other two. It is named after Greek mathematician Apollonius of Perga.-Construction:...
are named. In the 17th century René Descartes
René Descartes
René Descartes ; was a French philosopher and writer who spent most of his adult life in the Dutch Republic. He has been dubbed the 'Father of Modern Philosophy', and much subsequent Western philosophy is a response to his writings, which are studied closely to this day...
discovered Descartes' theorem
Descartes' theorem
In geometry, Descartes' theorem, named after René Descartes, establishes a relationship between four kissing, or mutually tangent, circles. The theorem can be used to construct a fourth circle tangent to three given, mutually tangent circles.-History:...
, a relationship between the reciprocals of the radii of mutually tangent circles.
Ford circles also appear in the Sangaku
Sangaku
Sangaku or San Gaku are Japanese geometrical puzzles in Euclidean geometry on wooden tablets which were placed as offerings at Shinto shrines or Buddhist temples during the Edo period by members of all social classes.-History:The Sangaku were painted in color on wooden tablets and hung in the...
(geometrical puzzles) of Japanese mathematics
Japanese mathematics
denotes a distinct kind of mathematics which was developed in Japan during the Edo Period . The term wasan, from wa and san , was coined in the 1870s and employed to distinguish native Japanese mathematics theory from Western mathematics .In the history of mathematics, the development of wasan...
. A typical problem, which is presented on an 1824 tablet in the Gunma Prefecture
Gunma Prefecture
is a prefecture of Japan located in the northwest corner of the Kantō region on Honshu island. Its capital is Maebashi.- History :The remains of a Paleolithic man were found at Iwajuku, Gunma Prefecture, in the early 20th century and there is a public museum there.Japan was without horses until...
, covers the relationship of three touching circles with a common tangent
Tangent
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
. Given the size of the two outer large circles, what is the size of the small circle between then? The answer is equivalent to a Ford circle:
Ford circles are named after American mathematician Lester R. Ford, Sr., who described them in an article in American Mathematical Monthly
American Mathematical Monthly
The American Mathematical Monthly is a mathematical journal founded by Benjamin Finkel in 1894. It is currently published 10 times each year by the Mathematical Association of America....
in 1938, volume 45, number 9, pages 586–601.
Properties
The Ford circle associated with the fraction p/q is denoted by C[p/q] or C[p, q]. There is a Ford circle associated with every rational numberRational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
. In addition, the line y = 1 is counted as a Ford circle – it can be thought of as the Ford circle associated with infinity
Infinity
Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
, which is the case p = 1, q = 0.
Two different Ford circles are either disjoint or tangent
Tangent
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
to one another. No two interiors of Ford circles intersect – even though there is a Ford circle tangent to the x-axis
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
at each point on it with rational
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
co-ordinates. If p/q is between 0 and 1, the Ford circles that are tangent to C[p/q] can be described variously as
- the circles C[r/s] where |ps − qr| = 1,
- the circles associated with the fractions r/s that are the neighbours of p/q in some Farey sequenceFarey sequenceIn mathematics, the Farey sequence of order n is the sequence of completely reduced fractions between 0 and 1 which, when in lowest terms, have denominators less than or equal to n, arranged in order of increasing size....
, or - the circles C[r/s] where r/s is the next larger or the next smaller ancestor to p/q in the Stern–Brocot tree or where p/q is the next larger or next smaller ancestor to r/s.
Ford circles can also be thought of as curves in the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
. The modular group of transformations of the complex plane maps Ford circles to other Ford circles.
By interpreting the upper half of the complex plane as a model of the hyperbolic plane
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
(the Poincaré half-plane model) Ford circles can also be interpreted as a tiling
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
of the hyperbolic plane by horocycle
Horocycle
In hyperbolic geometry, a horocycle is a curve whose normals all converge asymptotically. It is the two-dimensional example of a horosphere ....
s. Any two Ford circles are congruent
Congruence (geometry)
In geometry, two figures are congruent if they have the same shape and size. This means that either object can be repositioned so as to coincide precisely with the other object...
in hyperbolic geometry
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
. If C[p/q] and C[r/s] are tangent Ford circles, then the half-circle joining (p/q, 0) and (r/s, 0) that is perpendicular to the x-axis is a hyperbolic line that also passes through the point where the two circles are tangent to one another.
Ford circles are a sub-set of the circles in the Apollonian gasket
Apollonian gasket
In mathematics, an Apollonian gasket or Apollonian net is a fractal generated from triples of circles, where each circle is tangent to the other two. It is named after Greek mathematician Apollonius of Perga.-Construction:...
generated by the lines y = 0 and y = 1 and the circle C[0/1].
Total area of Ford circles
There is a link between the area of Ford circles, Euler's totient functionEuler's totient function
In number theory, the totient \varphi of a positive integer n is defined to be the number of positive integers less than or equal to n that are coprime to n In number theory, the totient \varphi(n) of a positive integer n is defined to be the number of positive integers less than or equal to n that...
φ and the Riemann zeta function.
As no two Ford circles intersect, it follows immediately that the total area of the Ford circles
is less than 1. In fact the total area of these Ford circles is given by a convergent sum, which can be evaluated.
From the definition, the area is
-
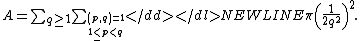
Simplifying this expression gives
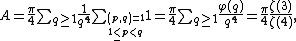
where the last equality reflects the Dirichlet generating function of φ(q) as documented on the page for Euler's totient functionEuler's totient functionIn number theory, the totient \varphi of a positive integer n is defined to be the number of positive integers less than or equal to n that are coprime to n In number theory, the totient \varphi(n) of a positive integer n is defined to be the number of positive integers less than or equal to n that...
.
Since ζ(4) = π 4/90, this finally becomes
This sum was discussed on es.ciencia.matematicas.
External links
- Art and graphics based on Ford circles
- Ford's Touching Circles at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- Fractions and Circles
- http://links.jstor.org/sici?sici=0002-9890%28193811%2945%3A9%3C586%3AF%3E2.0.CO%3B2-1Lester R. Ford's paper, "Fractions", American Mathematical MonthlyAmerican Mathematical MonthlyThe American Mathematical Monthly is a mathematical journal founded by Benjamin Finkel in 1894. It is currently published 10 times each year by the Mathematical Association of America....
, volume 45, number 9, pages 586–601, 1938]
-