Circles of Apollonius
Encyclopedia
The term circle of Apollonius is used to describe several types of circles associated with Apollonius of Perga
, a renowned Greek
geometer. Most of these circles are found in planar
Euclidean geometry
, but analogs have been defined on other surfaces; for example, counterparts on the surface of a sphere can be defined through stereographic projection
.
The main uses of this term are fivefold:
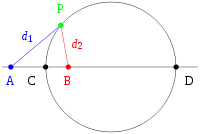
A circle is usually defined as the set of points P at a given distance r (the circle's radius) from a given point (the circle's center). However, there are other, equivalent definitions of a circle. Apollonius discovered that a circle could also be defined as the set of points P that have a given ratio of distances k = d1/d2 to two given points (labeled A and B in Figure 1). These two points are sometimes called the foci
.
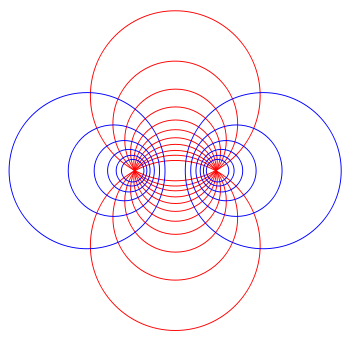
intersect each other at right angle
s and form the basis of the bipolar coordinate system
. Within each pencil, any two circles have the same radical axis
; the two radical axes of the two pencils are perpendicular, and the centers of the circles from one pencil lie on the radical axis of the other pencil.
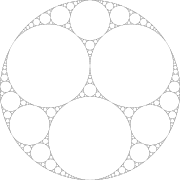By solving Apollonius' problem repeatedly to find the inscribed circle, the interstices between mutually tangential circles can be filled arbitrarily finely, forming an Apollonian gasket
, also known as a Leibniz packing or an Apollonian packing. This gasket is a fractal
, being self-similar and having a dimension
d that is not known exactly but is roughly 1.3,
which is higher than that of a regular (or rectifiable) curve (d=1) but less than that of a plane (d=2). The Apollonian gasket was first described by Gottfried Leibniz
in the 17th century, and is a curved precursor of the 20th-century Sierpiński triangle
. The Apollonian gasket also has deep connections to other fields of mathematics; for example, it is the limit set of Kleinian group
s.
defined by an arbitrary triangle 
. The circle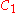 
is defined as the unique circle passing through the triangle vertex 
that maintains a constant ratio of distances to the other two vertices 
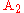and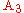 
(cf. Apollonius' definition of the circle
above). Similarly, the circle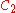
is defined as the unique circle passing through the triangle vertex 
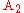that maintains a constant ratio of distances to the other two vertices 
and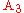 
, and so on for the circle 
.
All three circles intersect the circumcircle of the triangle
orthogonally. All three circles pass through two points, denoted as the isodynamic point
s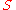
and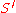 
of the triangle. The line connecting these common intersection points is the radical axis
for all three circles. The two isodynamic points are inverses of each other relative to the circumcircle of the triangle.
Remarkably, the centers of these three circles fall on a single line (the Lemoine line). This line is perpendicular to the radical axis defined by the isodynamic point
s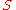
and 
.
Apollonius of Perga
Apollonius of Perga [Pergaeus] was a Greek geometer and astronomer noted for his writings on conic sections. His innovative methodology and terminology, especially in the field of conics, influenced many later scholars including Ptolemy, Francesco Maurolico, Isaac Newton, and René Descartes...
, a renowned Greek
Ancient Greece
Ancient Greece is a civilization belonging to a period of Greek history that lasted from the Archaic period of the 8th to 6th centuries BC to the end of antiquity. Immediately following this period was the beginning of the Early Middle Ages and the Byzantine era. Included in Ancient Greece is the...
geometer. Most of these circles are found in planar
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
Euclidean geometry
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
, but analogs have been defined on other surfaces; for example, counterparts on the surface of a sphere can be defined through stereographic projection
Stereographic projection
The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it...
.
The main uses of this term are fivefold:
- Apollonius showed that a circle can be defined as the set of points in a plane that have a specified ratio of distances to two fixed points known as fociFocus (geometry)In geometry, the foci are a pair of special points with reference to which any of a variety of curves is constructed. For example, foci can be used in defining conic sections, the four types of which are the circle, ellipse, parabola, and hyperbola...
. This circle of Apollonius is the basis of the Apollonius pursuit problem.
- The Apollonian circlesApollonian circlesApollonian circles are two families of circles such that every circle in the first family intersects every circle in the second family orthogonally, and vice versa. These circles form the basis for bipolar coordinates...
are two families of mutually orthogonal circles. The first family consists of the circles with all possible distance ratios to two fixed foci, whereas the second family consists of all possible circles that pass through both foci. These circles form the basis of bipolar coordinatesBipolar coordinatesBipolar coordinates are a two-dimensional orthogonal coordinate system. There are two commonly defined types of bipolar coordinates. The other system is two-center bipolar coordinates. There is also a third coordinate system that is based on two poles . The first is based on the Apollonian circles...
.
- Apollonius' problemProblem of ApolloniusIn Euclidean plane geometry, Apollonius' problem is to construct circles that are tangent to three given circles in a plane . Apollonius of Perga posed and solved this famous problem in his work ; this work has been lost, but a 4th-century report of his results by Pappus of Alexandria has survived...
is to construct circles that are simultaneously tangent to three specified circles. The solutions to this problem are sometimes called the "circles of Apollonius".
- The Apollonian gasketApollonian gasketIn mathematics, an Apollonian gasket or Apollonian net is a fractal generated from triples of circles, where each circle is tangent to the other two. It is named after Greek mathematician Apollonius of Perga.-Construction:...
—one of the first fractalFractalA fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
s ever described—is a set of mutually tangent circles, formed by solving Apollonius' problem iteratively.
- The isodynamic pointIsodynamic pointIn Euclidean geometry, every triangle has two isodynamic points, usually denoted as S and S^'. These points are the common intersection points of the three circles of Apollonius associated with the triangle; hence, the line through these points is the common radical axis for these circles...
s and Lemoine line of a triangle can be solved using three circles, each of which passes through one vertex of the triangle and maintains a constant ratio of distances to the other two.
Apollonius' definition of a circle
A circle is usually defined as the set of points P at a given distance r (the circle's radius) from a given point (the circle's center). However, there are other, equivalent definitions of a circle. Apollonius discovered that a circle could also be defined as the set of points P that have a given ratio of distances k = d1/d2 to two given points (labeled A and B in Figure 1). These two points are sometimes called the foci
Focus (geometry)
In geometry, the foci are a pair of special points with reference to which any of a variety of curves is constructed. For example, foci can be used in defining conic sections, the four types of which are the circle, ellipse, parabola, and hyperbola...
.
Apollonius pursuit problem
The Apollonius pursuit problem is one of finding where a ship leaving from one point A at speed v1 will intercept another ship leaving a different point B at speed v2. By assumption, the ships travel in straight lines and the ratio of their speeds is denoted as k = v1/v2. At the point they meet, the first ship will have traveled a k-fold longer distance than the second ship. Therefore, the point must lie on a circle as defined by Apollonius, with their starting points as the foci.Circles sharing a radical axis
The circles defined by the Apollonian pursuit problem for the same two points A and B, but with varying ratios of the two speeds, are disjoint from each other and form a continuous family that cover the entire plane; this family of circles is known as a hyperbolic pencil. Another family of circles, the circles that pass through both A and B, are also called a pencil, or more specifically an elliptic pencil. These two pencils of Apollonian circlesApollonian circles
Apollonian circles are two families of circles such that every circle in the first family intersects every circle in the second family orthogonally, and vice versa. These circles form the basis for bipolar coordinates...
intersect each other at right angle
Right angle
In geometry and trigonometry, a right angle is an angle that bisects the angle formed by two halves of a straight line. More precisely, if a ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles...
s and form the basis of the bipolar coordinate system
Bipolar coordinates
Bipolar coordinates are a two-dimensional orthogonal coordinate system. There are two commonly defined types of bipolar coordinates. The other system is two-center bipolar coordinates. There is also a third coordinate system that is based on two poles . The first is based on the Apollonian circles...
. Within each pencil, any two circles have the same radical axis
Radical axis
The radical axis of two circles is the locus of points at which tangents drawn to both circles have the same length. For any point P on the radical axis, there is a unique circle centered on P that intersects both circles at right angles ; conversely, the center of any circle that cuts both...
; the two radical axes of the two pencils are perpendicular, and the centers of the circles from one pencil lie on the radical axis of the other pencil.
Solutions to Apollonius' problem
Apollonian gasket
Apollonian gasket
In mathematics, an Apollonian gasket or Apollonian net is a fractal generated from triples of circles, where each circle is tangent to the other two. It is named after Greek mathematician Apollonius of Perga.-Construction:...
, also known as a Leibniz packing or an Apollonian packing. This gasket is a fractal
Fractal
A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
, being self-similar and having a dimension
Hausdorff dimension
thumb|450px|Estimating the Hausdorff dimension of the coast of Great BritainIn mathematics, the Hausdorff dimension is an extended non-negative real number associated with any metric space. The Hausdorff dimension generalizes the notion of the dimension of a real vector space...
d that is not known exactly but is roughly 1.3,
which is higher than that of a regular (or rectifiable) curve (d=1) but less than that of a plane (d=2). The Apollonian gasket was first described by Gottfried Leibniz
Gottfried Leibniz
Gottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
in the 17th century, and is a curved precursor of the 20th-century Sierpiński triangle
Sierpinski triangle
The Sierpinski triangle , also called the Sierpinski gasket or the Sierpinski Sieve, is a fractal and attractive fixed set named after the Polish mathematician Wacław Sierpiński who described it in 1915. However, similar patterns appear already in the 13th-century Cosmati mosaics in the cathedral...
. The Apollonian gasket also has deep connections to other fields of mathematics; for example, it is the limit set of Kleinian group
Kleinian group
In mathematics, a Kleinian group is a discrete subgroup of PSL. The group PSL of 2 by 2 complex matrices of determinant 1 modulo its center has several natural representations: as conformal transformations of the Riemann sphere, and as orientation-preserving isometries of 3-dimensional hyperbolic...
s.
Isodynamic points of a triangle
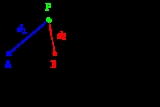
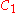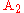Circles of Apollonius may be used as a technical term to denote three special circles defined by an arbitrary triangle . The circle is defined as the unique circle passing through the triangle vertex that maintains a constant ratio of distances to the other two vertices and 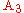(cf. Apollonius' definition of the circleCircle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
above). Similarly, the circle
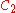is defined as the unique circle passing through the triangle vertex 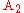that maintains a constant ratio of distances to the other two vertices and 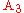, and so on for the circle .All three circles intersect the circumcircle of the triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
orthogonally. All three circles pass through two points, denoted as the isodynamic point
Isodynamic point
In Euclidean geometry, every triangle has two isodynamic points, usually denoted as S and S^'. These points are the common intersection points of the three circles of Apollonius associated with the triangle; hence, the line through these points is the common radical axis for these circles...
s
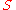and 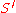of the triangle. The line connecting these common intersection points is the radical axisRadical axis
The radical axis of two circles is the locus of points at which tangents drawn to both circles have the same length. For any point P on the radical axis, there is a unique circle centered on P that intersects both circles at right angles ; conversely, the center of any circle that cuts both...
for all three circles. The two isodynamic points are inverses of each other relative to the circumcircle of the triangle.
Remarkably, the centers of these three circles fall on a single line (the Lemoine line). This line is perpendicular to the radical axis defined by the isodynamic point
Isodynamic point
In Euclidean geometry, every triangle has two isodynamic points, usually denoted as S and S^'. These points are the common intersection points of the three circles of Apollonius associated with the triangle; hence, the line through these points is the common radical axis for these circles...
s
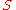and .