Packing problem
Encyclopedia
Packing problems are a class of optimization problems in mathematics
which involve attempting to pack objects together (often inside a container), as densely as possible. Many of these problems can be related to real life packaging, storage and transportation issues. Each packing problem has a dual covering problem
, which asks how many of the same objects are required to completely cover every region of the container, where objects are allowed to overlap.
In a packing problem, you are given:
Usually the packing must be without overlaps between goods and other goods or the container walls. The aim is to find the configuration with the maximal density. In some variants the overlapping (of goods with each other and/or with the boundary of the container) is allowed but should be minimized.
. This problem is relevant to a number of scientific disciplines, and has received significant attention. The Kepler conjecture
postulated an optimal solution for packing spheres
hundreds of years before it was proven correct by Thomas Callister Hales
. Many other shapes have received attention, including ellipsoids, Platonic and Archimedean solids including tetrahedra
, and unequal-sphere dimers.
.svg.png)
These problems are mathematically distinct from the ideas in the circle packing theorem
. The related circle packing
problem deals with packing circles, possibly of different sizes, on a surface, for instance the plane or a sphere.
The counterparts of a circle in other dimensions can never be packed with complete efficiency in dimensions
larger than one (in a one dimensional universe, the circle analogue is just two points). That is, there will always be unused space if you are only packing circles. The most efficient way of packing circles, hexagonal packing
, produces approximately 91% efficiency.http://mathworld.wolfram.com/CirclePacking.html
and 24-dimensional Leech lattice
are also believed to be optimal.
. No other Platonic solid
can tile space on its own, but some preliminary results are known. Tetrahedra
can achieve a packing of at least 85%. One of the best packings of regular dodecahedra is based on the aforementioned face-centered cubic (FCC) lattice.
Tetrahedra and octahedra together can fill all of space in an arrangement known as the tetrahedral-octahedral honeycomb
.
disjoint open unit balls may be packed inside it has a simple and complete answer in 
-dimensional Euclidean space if 
, and in an infinite dimensional Hilbert space with no restrictions. It is worth describing in detail here, to give a flavor of the general problem. In this case, a configuration of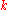 
pairwise tangent unit balls is available. Place the centers at the vertices 
of a regular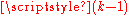 
dimensional simplex with edge 2; this is easily realized starting from an orthonormal basis. A small computation shows that the distance of each vertex from the barycenter is 
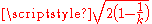. Moreover, any other point of the space necessarily has a larger distance from at least one of the 
vertices. In terms of inclusions of balls, the 
open unit balls centered at 
are included in a ball of radius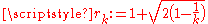 
, which is minimal for this configuration.
To show that this configuration is optimal, let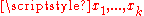
be the centers of 
disjoint open unit balls contained in a ball of radius 
centered at a point 
. Consider the map from the finite set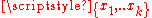 
into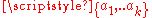 
taking 
in the corresponding 
for each 
. Since for all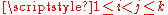 
, 
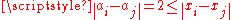this map is 1-Lipschitz and by the Kirszbraun theorem
it extends to a 1-Lipschitz map that is globally defined; in particular, there exists a point
such that for all 
one has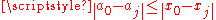 
, so that also 
. This shows that there are 
disjoint unit open balls in a ball of radius 
if and only if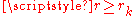 
. Notice that in an infinite dimensional Hilbert space this implies that there are infinitely many disjoint open unit balls inside a ball of radius 
if and only if 
. For instance, the unit balls centered at 
, where 
is an orthonormal basis, are disjoint and included in a ball of radius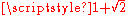 
centered at the origin. Moreover, for 
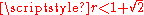, the maximum number of disjoint open unit balls inside a ball of radius r is 
.
objects of given diameter d can be packed into a cuboid
of size a × b × c.
Optimal solutions have been proven for n≤13, and n=19.
. This is closely related to spreading points in a unit square with the objective of finding the greatest minimal separation, dn, between points. To convert between these two formulations of the problem, the square side for unit circles will be L=2+2/dn.
Optimal solutions have been proven for n≤30.
.
Optimal solutions have been proven for n=1-10, 14-16, 23-25, 34-36, 62-64, 79-81, 98-100, and any square integer.
The wasted space is asymptotically o
(a7/11).
Minimum solutions:
For example, it is possible to pack 147 rectangles of size (137,95) in a rectangle of size (1600,1230).
An example of a fast algorithm that packs rectangles of varying widths and heights into an enclosing rectangle of minimum area is here.
There are significant theorems on tiling rectangles (and cuboids) in rectangles (cuboids) with no gaps or overlaps:
The study of polyomino
tilings largely concerns two classes of problems: to tile a rectangle with congruent tiles, and to pack one of each n-omino into a rectangle.
A classic puzzle of the second kind is to arrange all twelve pentomino
es into rectangles sized 3×20, 4×15, 5×12 or 6×10.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
which involve attempting to pack objects together (often inside a container), as densely as possible. Many of these problems can be related to real life packaging, storage and transportation issues. Each packing problem has a dual covering problem
Covering problem
In combinatorics and computer science, covering problems are computational problems that ask whether a certain combinatorial structure 'covers' another, or how large the structure has to be to do that....
, which asks how many of the same objects are required to completely cover every region of the container, where objects are allowed to overlap.
In a packing problem, you are given:
- 'containers' (usually a single two- or three-dimensional convex region, or an infinite space)
- 'goods' (usually a single type of shape), some or all of which must be packed into this container
Usually the packing must be without overlaps between goods and other goods or the container walls. The aim is to find the configuration with the maximal density. In some variants the overlapping (of goods with each other and/or with the boundary of the container) is allowed but should be minimized.
Packing infinite space
Many of these problems, when the container size is increased in all directions, become equivalent to the problem of packing objects as densely as possible in infinite Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. This problem is relevant to a number of scientific disciplines, and has received significant attention. The Kepler conjecture
Kepler conjecture
The Kepler conjecture, named after the 17th-century German astronomer Johannes Kepler, is a mathematical conjecture about sphere packing in three-dimensional Euclidean space. It says that no arrangement of equally sized spheres filling space has a greater average density than that of the cubic...
postulated an optimal solution for packing spheres
Sphere packing
In geometry, a sphere packing is an arrangement of non-overlapping spheres within a containing space. The spheres considered are usually all of identical size, and the space is usually three-dimensional Euclidean space...
hundreds of years before it was proven correct by Thomas Callister Hales
Thomas Callister Hales
Thomas Callister Hales is an American mathematician. He is known for his 1998 computer-aided proof of the Kepler conjecture, a centuries-old problem in discrete geometry which states that the most space-efficient way to pack spheres is in a pyramid shape...
. Many other shapes have received attention, including ellipsoids, Platonic and Archimedean solids including tetrahedra
Tetrahedron packing
In geometry, tetrahedron packing is the problem of arranging identical regular tetrahedra throughout three-dimensional space so as to fill the maximum possible fraction of space....
, and unequal-sphere dimers.
Hexagonal packing of circles
Circle packing theorem
The circle packing theorem describes the possible tangency relations between circles in the plane whose interiors are disjoint. A circle packing is a connected collection of circles whose interiors are disjoint...
. The related circle packing
Circle packing
In geometry, circle packing is the study of the arrangement of circles on a given surface such that no overlapping occurs and so that all circles touch another. The associated "packing density", η of an arrangement is the proportion of the surface covered by the circles...
problem deals with packing circles, possibly of different sizes, on a surface, for instance the plane or a sphere.
The counterparts of a circle in other dimensions can never be packed with complete efficiency in dimensions
Dimensions
Dimensions is a French project that makes educational movies about mathematics, focusing on spatial geometry. It uses POV-Ray to render some of the animations, and the films are release under a Creative Commons licence....
larger than one (in a one dimensional universe, the circle analogue is just two points). That is, there will always be unused space if you are only packing circles. The most efficient way of packing circles, hexagonal packing
Circle packing
In geometry, circle packing is the study of the arrangement of circles on a given surface such that no overlapping occurs and so that all circles touch another. The associated "packing density", η of an arrangement is the proportion of the surface covered by the circles...
, produces approximately 91% efficiency.http://mathworld.wolfram.com/CirclePacking.html
Sphere packings in higher dimensions
In three dimensions, the face-centered cubic lattice offers the best lattice packing of spheres, and is believed to be the optimal of all packings. The 8-dimensional E8 latticeE8 lattice
In mathematics, the E8 lattice is a special lattice in R8. It can be characterized as the unique positive-definite, even, unimodular lattice of rank 8...
and 24-dimensional Leech lattice
Leech lattice
In mathematics, the Leech lattice is an even unimodular lattice Λ24 in 24-dimensional Euclidean space E24 found by .-History:Many of the cross-sections of the Leech lattice, including the Coxeter–Todd lattice and Barnes–Wall lattice, in 12 and 16 dimensions, were found much earlier than...
are also believed to be optimal.
Packings of Platonic solids in three dimensions
Cubes can easily be arranged to fill three-dimensional space completely, the most natural packing being the cubic honeycombCubic honeycomb
The cubic honeycomb is the only regular space-filling tessellation in Euclidean 3-space, made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron....
. No other Platonic solid
Platonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
can tile space on its own, but some preliminary results are known. Tetrahedra
Tetrahedron packing
In geometry, tetrahedron packing is the problem of arranging identical regular tetrahedra throughout three-dimensional space so as to fill the maximum possible fraction of space....
can achieve a packing of at least 85%. One of the best packings of regular dodecahedra is based on the aforementioned face-centered cubic (FCC) lattice.
Tetrahedra and octahedra together can fill all of space in an arrangement known as the tetrahedral-octahedral honeycomb
Tetrahedral-octahedral honeycomb
The tetrahedral-octahedral honeycomb or alternated cubic honeycomb is a space-filling tessellation in Euclidean 3-space. It is composed of alternating octahedra and tetrahedra in a ratio of 1:2....
.
| Solid | Maximum known packing density | Lowest upper bound for lattice packing density |
|---|---|---|
| icosahedra | 0.836315 | 0.836357 |
| dodecahedra | 0.904002 | (5+sqrt(5))/8=0.904508 |
| octahedra | 0.947003 | 18/19 = 0.947368 |
Spheres into a Euclidean ball
The problem of finding the smallest ball such that disjoint open unit balls may be packed inside it has a simple and complete answer in -dimensional Euclidean space if , and in an infinite dimensional Hilbert space with no restrictions. It is worth describing in detail here, to give a flavor of the general problem. In this case, a configuration of 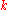pairwise tangent unit balls is available. Place the centers at the vertices of a regular 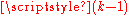dimensional simplex with edge 2; this is easily realized starting from an orthonormal basis. A small computation shows that the distance of each vertex from the barycenter is 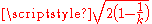. Moreover, any other point of the space necessarily has a larger distance from at least one of the vertices. In terms of inclusions of balls, the open unit balls centered at are included in a ball of radius 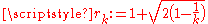, which is minimal for this configuration.To show that this configuration is optimal, let
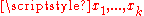be the centers of disjoint open unit balls contained in a ball of radius centered at a point . Consider the map from the finite set 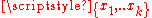into 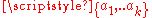taking in the corresponding for each . Since for all 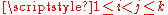, 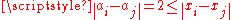this map is 1-Lipschitz and by the Kirszbraun theoremKirszbraun theorem
In mathematics, specifically real analysis and functional analysis, the Kirszbraun theorem states that if U is a subset of some Hilbert space H1, and H2 is another Hilbert space, and...
it extends to a 1-Lipschitz map that is globally defined; in particular, there exists a point
such that for all one has 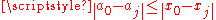, so that also . This shows that there are disjoint unit open balls in a ball of radius if and only if 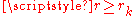. Notice that in an infinite dimensional Hilbert space this implies that there are infinitely many disjoint open unit balls inside a ball of radius if and only if . For instance, the unit balls centered at , where is an orthonormal basis, are disjoint and included in a ball of radius 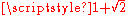centered at the origin. Moreover, for 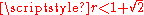, the maximum number of disjoint open unit balls inside a ball of radius r is .Spheres in a cuboid
Determine the number of sphericalSphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
objects of given diameter d can be packed into a cuboid
Cuboid
In geometry, a cuboid is a solid figure bounded by six faces, forming a convex polyhedron. There are two competing definitions of a cuboid in mathematical literature...
of size a × b × c.
Circles in circle
Pack n unit circles into the smallest possible circle. This is closely related to spreading points in a unit circle with the objective of finding the greatest minimal separation, dn, between points.Optimal solutions have been proven for n≤13, and n=19.
Circles in square
Pack n unit circles into the smallest possible squareSquare (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
. This is closely related to spreading points in a unit square with the objective of finding the greatest minimal separation, dn, between points. To convert between these two formulations of the problem, the square side for unit circles will be L=2+2/dn.
Optimal solutions have been proven for n≤30.
Circles in isosceles right triangle
Pack n unit circles into the smallest possible isosceles right triangle. Good estimates are known for n<300.Circles in equilateral triangle
Pack n unit circles into the smallest possible equilateral triangle. Optimal solutions are known for n<13, and conjectures are avaiable for n<28.Squares in square
Pack n unit squares into the smallest possible squareSquare (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
.
Optimal solutions have been proven for n=1-10, 14-16, 23-25, 34-36, 62-64, 79-81, 98-100, and any square integer.
The wasted space is asymptotically o
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
(a7/11).
Squares in circle
Pack n squares in the smallest possible circle.Minimum solutions:
| Number of squares | Circle radius |
|---|---|
| 1 | 0.707... |
| 2 | 1.118... |
| 3 | 1.288... |
| 4 | 1.414... |
| 5 | 1.581... |
| 6 | 1.688... |
| 7 | 1.802... |
| 8 | 1.978... |
| 9 | 2.077... |
| 10 | 2.121... |
| 11 | 2.215... |
| 12 | 2.236... |
Identical rectangles in a rectangle
The problem of packing multiple instances of a single rectangle of size (l,w), allowing for 90o rotation, in a bigger rectangle of size (L,W) has some applications such as loading of boxes on pallets and, specifically, woodpulp stowage.For example, it is possible to pack 147 rectangles of size (137,95) in a rectangle of size (1600,1230).
Different rectangles in a rectangle
The problem of packing multiple rectangles of varying widths and heights in an enclosing rectangle of minimum area (but with no boundaries on the enclosing rectangle's width or height) has an important application in combining images into a single larger image. A web page that loads a single larger image often renders faster in the browser than the same page loading multiple small images, due to the overhead involved in requesting each image from the web server.An example of a fast algorithm that packs rectangles of varying widths and heights into an enclosing rectangle of minimum area is here.
Related fields
In tiling or tesselation problems, there are to be no gaps, nor overlaps. Many of the puzzles of this type involve packing rectangles or polyominoes into a larger rectangle or other square-like shape.There are significant theorems on tiling rectangles (and cuboids) in rectangles (cuboids) with no gaps or overlaps:
- Klarner's theorem: An a × b rectangle can be packed with 1 × n strips iff n | a or n | b.
- de Bruijn's theoremDe Bruijn's theoremDe Bruijn's theorem is a theorem concerning computational geometry and packing problems attributed to Nicolaas Govert de Bruijn.-Theorem:A box can be packed with a brick a×ab×abc if and only if the box has dimensions ap×abq×abcr for some natural numbers p, q, r....
: A box can be packed with a harmonic brick a × a b × a b c if the box has dimensions a p × a b q × a b c r for some natural numberNatural numberIn mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s p, q, r (i.e., the box is a multiple of the brick.)
The study of polyomino
Polyomino
A polyomino is a plane geometric figure formed by joining one or more equal squares edge to edge. It is a polyform whose cells are squares. It may be regarded as a finite subset of the regular square tiling with a connected interior....
tilings largely concerns two classes of problems: to tile a rectangle with congruent tiles, and to pack one of each n-omino into a rectangle.
A classic puzzle of the second kind is to arrange all twelve pentomino
Pentomino
A pentomino is a polyomino composed of five congruent squares, connected along their edges ....
es into rectangles sized 3×20, 4×15, 5×12 or 6×10.
Packing of irregular objects
Packing of irregular objects is a problem not lending itself well to closed form solutions; however, the applicability to practical environmental science is quite important. For example, irregularly shaped soil particles pack differently as the sizes and shapes vary, leading to important outcomes for plant species to adapt root formations and to allow water movement in the soil.See also
- Set packingSet packingSet packing is a classical NP-complete problem in computational complexity theory and combinatorics, and was one of Karp's 21 NP-complete problems.Suppose we have a finite set S and a list of subsets of S...
- Bin packing problemBin packing problemIn computational complexity theory, the bin packing problem is a combinatorial NP-hard problem. In it, objects of different volumes must be packed into a finite number of bins of capacity V in a way that minimizes the number of bins used....
- Slothouber-Graatsma puzzle
- Conway puzzleConway puzzleConway's puzzle is a packing problem using rectangular blocks, named after its inventor, mathematician John Conway. It calls for packing thirteen 1 × 2 × 4 blocks, one 2 × 2 × 2 block, one 1 × 2 × 2 block, and three 1 × 1 × 3 blocks into a 5 × 5 × 5 box....
- TetrisTetrisTetris is a puzzle video game originally designed and programmed by Alexey Pajitnov in the Soviet Union. It was released on June 6, 1984, while he was working for the Dorodnicyn Computing Centre of the Academy of Science of the USSR in Moscow, Russian Soviet Federative Socialist Republic...
- Covering problemCovering problemIn combinatorics and computer science, covering problems are computational problems that ask whether a certain combinatorial structure 'covers' another, or how large the structure has to be to do that....
- Knapsack problemKnapsack problemThe knapsack problem or rucksack problem is a problem in combinatorial optimization: Given a set of items, each with a weight and a value, determine the count of each item to include in a collection so that the total weight is less than or equal to a given limit and the total value is as large as...
- Tetrahedron packingTetrahedron packingIn geometry, tetrahedron packing is the problem of arranging identical regular tetrahedra throughout three-dimensional space so as to fill the maximum possible fraction of space....
- Cutting stock problemCutting stock problemThe cutting-stock problem is an optimization problem, or more specifically, an integer linear programming problem. It arises from many applications in industry. Imagine that you work in a paper mill and you have a number of rolls of paper of fixed width waiting to be cut, yet different customers...
- Kissing number problemKissing number problemIn geometry, a kissing number is defined as the number of non-overlapping unit spheres that touch another given unit sphere. For a lattice packing the kissing number is the same for every sphere, but for an arbitrary sphere packing the kissing number may vary from one sphere to another...
External links
Many puzzle books as well as mathematical journals contain articles on packing problems.- Links to various MathWorld articles on packing
- MathWorld notes on packing squares.
- Erich's Packing Center
- www.packomania.com A site with tables, graphs, calculators, references, etc.
- "Box Packing" by Ed Pegg, Jr.Ed Pegg, Jr.Ed Pegg, Jr. is an expert on mathematical puzzles and is a self-described recreational mathematician. He creates puzzles for the Mathematical Association of America online at Ed Pegg, Jr.'s Math Games. His puzzles have also been used by Will Shortz on the puzzle segment of NPR's Weekend Edition...
, the Wolfram Demonstrations ProjectWolfram Demonstrations ProjectThe Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...
, 2007. - Best known packings of equal circles in a circle, up to 1100