
Steiner chain
Encyclopedia

Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a Steiner chain is a set of n circles, all of which are tangent to two given non-intersecting circles (blue and red in Figure 1), where n is finite and each circle in the chain is tangent to the previous and next circles in the chain. In the usual closed Steiner chains, the first and last (nth) circles are also tangent to each other; by contrast, in open Steiner chains, they need not be. The given circles α and β do not intersect, but otherwise are unconstrained; the smaller circle may lie completely inside or outside of the larger circle. In these cases, the centers of Steiner-chain circles lie on an ellipse
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
or a hyperbola
Hyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
, respectively.
Steiner chains are named after Jakob Steiner
Jakob Steiner
Jakob Steiner was a Swiss mathematician who worked primarily in geometry.-Personal and professional life:...
, who defined them in the 19th century and discovered many of their properties. A fundamental result is Steiner's porism
Porism
A porism is a mathematical proposition or corollary. In particular, the term porism has been used to refer to a direct result of a proof, analogous to how a corollary refers to a direct result of a theorem.-Beginnings:...
, which states:
-
- If at least one closed Steiner chain of n circles exists for two given circles α and β, then there is an infinite number of closed Steiner chains of n circles; and any circle tangent to α and β in the same way is a member of such a chain.
"Tangent in the same way" means that the arbitrary circle is internally or externally tangent in the same way as a circle of the original Steiner chain. A porism is a type of theorem relating to the number of solutions and the conditions on it. Porisms often describe a geometrical figure that cannot exist unless a condition is met, but otherwise may exist in infinite number; another example is Poncelet's porism
Poncelet's porism
In geometry, Poncelet's porism, named after French engineer and mathematician Jean-Victor Poncelet, states the following: Let C and D be two plane conics...
.
The method of circle inversion is helpful in treating Steiner chains. Since it preserves tangencies, angles and circles, inversion transforms one Steiner chain into another of the same number of circles. One particular choice of inversion transforms the given circles α and β into concentric circles; in this case, all the circles of the Steiner chain have the same size and can "roll" around in the annulus
Annulus (mathematics)
In mathematics, an annulus is a ring-shaped geometric figure, or more generally, a term used to name a ring-shaped object. Or, it is the area between two concentric circles...
between the circles similar to ball bearing
Ball bearing
A ball bearing is a type of rolling-element bearing that uses balls to maintain the separation between the bearing races.The purpose of a ball bearing is to reduce rotational friction and support radial and axial loads. It achieves this by using at least two races to contain the balls and transmit...
s. This standard configuration allows several properties of Steiner chains to be derived, e.g., its points of tangencies always lie on a circle. Several generalizations of Steiner chains exist, most notably Soddy's hexlet
Soddy's hexlet
In geometry, Soddy's hexlet is a chain of six spheres , each of which is tangent to both of its neighbors and also to three mutually tangent given spheres. In Figure 1, these three spheres are shown as an outer circumscribing sphere C , and two spheres A and B above and below the plane of their...
and Pappus chain
Pappus chain
In geometry, the Pappus chain was created by Pappus of Alexandria in the 3rd century AD.-Construction:The arbelos is defined by two circles, CU and CV, which are tangent at the point A and where CU is enclosed by CV...
s.
Definitions and types of tangency
The two given circles α and β cannot intersect; hence, the smaller given circle must lie inside or outside the larger. The circles are usually shown as an annulus
Annulus (mathematics)
In mathematics, an annulus is a ring-shaped geometric figure, or more generally, a term used to name a ring-shaped object. Or, it is the area between two concentric circles...
, i.e., with the smaller given circle inside the larger one. In this configuration, the Steiner-chain circles are externally tangent to the inner given circle and internally tangent to the outer circle. However, the smaller circle may also lie completely outside the larger one (Figure 2). The black circles of Figure 2 satisfy the conditions for a closed Steiner chain: they are all tangent to the two given circles and each is tangent to its neighbors in the chain. In this configuration, the Steiner-chain circles have the same type of tangency to both given circles, either externally or internally tangent to both. If the two given circles are tangent at a point, the Steiner chain becomes an infinite Pappus chain
Pappus chain
In geometry, the Pappus chain was created by Pappus of Alexandria in the 3rd century AD.-Construction:The arbelos is defined by two circles, CU and CV, which are tangent at the point A and where CU is enclosed by CV...
, which is often discussed in the context of the arbelos
Arbelos
In geometry, an arbelos is a plane region bounded by a semicircle of diameter 1, connected to semicircles of diameters r and , all oriented the same way and sharing a common baseline. Archimedes is believed to be the first mathematician to study its mathematical properties, as it appears in...
(shoemaker's knife), a geometric figure made from three circles. There is no general name for a sequence of circles tangent to two given circles that intersect at two points.
Closed, open and multi-cyclic
The two given circles α and β touch the n circles of the Steiner chain, but each circle Ck of a Steiner chain touches only four circles: α, β, and its two neighbors, Ck−1 and Ck+1. By default, Steiner chains are assumed to be closed, i.e., the first and last circles are tangent to one another. By contrast, an open Steiner chain is one in which the first and last circles, C1 and Cn, are not tangent to one another; these circles are tangent only to three circles. Multicyclic Steiner chains wrap around the inner circle several times before closing, i.e., before being tangent to the initial circle.
Annular case and feasibility criterion
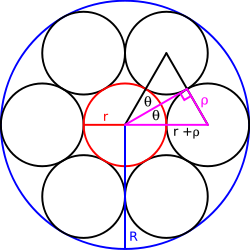
Annulus (mathematics)
In mathematics, an annulus is a ring-shaped geometric figure, or more generally, a term used to name a ring-shaped object. Or, it is the area between two concentric circles...
between them. By symmetry, the angle 2θ between the centers of the Steiner-chain circles is 360°/n. Because Steiner chain circles are tangent to one another, the distance between their centers equals the sum of their radii, here twice their radius ρ. The bisector (green in Figure) creates two right triangles, with a central angle of . The sine
Sine
In mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
of this angle can be written as the length of its opposite segment, divided by the hypotenuse of the right triangle
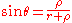
Since θ is known from n, this provides an equation for the unknown radius ρ of the Steiner-chain circles
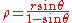
The tangent points of a Steiner chain circle with the inner and outer given circles lie on a line that pass through their common center; hence, the outer radius .
These equations provide a criterion for the feasibility of a Steiner chain for two given concentric circles. A closed Steiner chain of n circles requires that the ratio of radii R/r of the given circles equal exactly
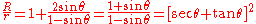
As shown below, this ratio-of-radii criterion for concentric given circles can be extended to all types of given circles by the inversive distance
Inversive distance
Inversive distance is a way of measuring the "distance" between two non-intersecting circles α and β. If α and β are inverted with respect to a circle centered at one of the limiting points of the pencil of α and β, then α and β will invert into concentric circles...
δ of the two given circles. For concentric circles, this distance is defined as a logarithm of their ratio of radii
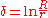
Using the solution for concentric circles, the general criterion for a Steiner chain of n circles can be written

If a multicyclic annular Steiner chain has n total circles and wraps around m times before closing, the angle between Steiner-chain circles equals
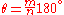
In other respects, the feasibility criterion is unchanged.
Properties under inversion
Circle inversion transforms one Steiner chain into another with the same number of circles.
In the transformed chain, the tangent points between adjacent circles of the Steiner chain all lie on a circle, namely the concentric circle midway between the two fixed concentric circles. Since tangencies and circles are preserved under inversion, this property of all tangencies lying on a circle is also true in the original chain. This property is also shared with the Pappus chain
Pappus chain
In geometry, the Pappus chain was created by Pappus of Alexandria in the 3rd century AD.-Construction:The arbelos is defined by two circles, CU and CV, which are tangent at the point A and where CU is enclosed by CV...
of circles, which can be construed as a special limiting case of the Steiner chain.
In the transformed chain, the tangent lines from O to the Steiner chain circles are separated by equal angles. In the original chain, this corresponds to equal angles between the tangent circles that pass through the center of inversion used to transform the original circles into a concentric pair.
In the transformed chain, the n lines connecting the pairs of tangent points of the Steiner circles with the concentric circles all pass through O, the common center. Similarly, the n lines tangent to each pair of adjacent circles in the Steiner chain also pass through O. Since lines through the center of inversion are invariant under inversion, and since tangency and concurrence are preserved under inversion, the 2n lines connecting the corresponding points in the original chain also pass through a single point, O.
Infinite family
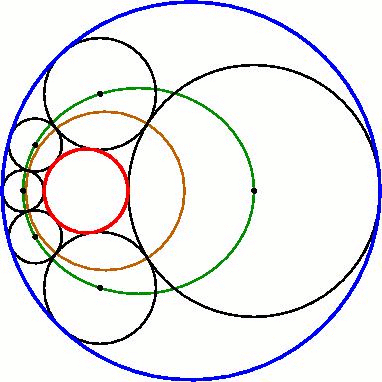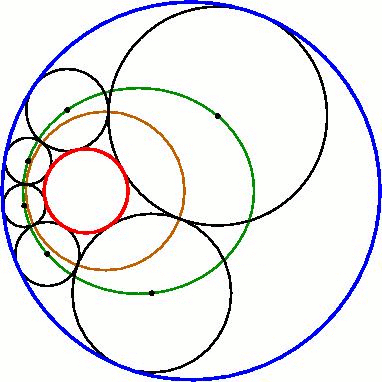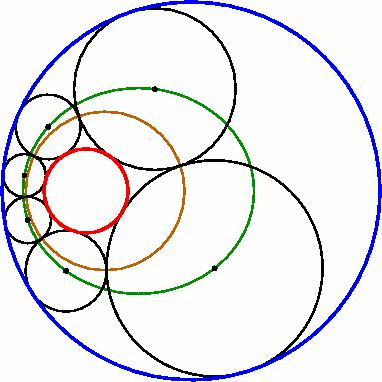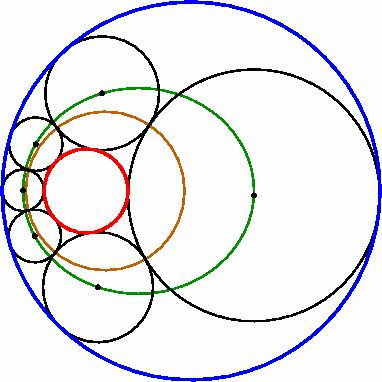
Elliptical/hyperbolic locus of centers
The centers of the circles of a Steiner chain lie on a conic sectionConic section
In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
. For example, if the smaller given circle lies within the larger, the centers lie on an ellipse
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
. This is true for any set of circles that are internally tangent to one given circle and externally tangent to the other; such systems of circles appear in the Pappus chain
Pappus chain
In geometry, the Pappus chain was created by Pappus of Alexandria in the 3rd century AD.-Construction:The arbelos is defined by two circles, CU and CV, which are tangent at the point A and where CU is enclosed by CV...
, the problem of Apollonius
Problem of Apollonius
In Euclidean plane geometry, Apollonius' problem is to construct circles that are tangent to three given circles in a plane . Apollonius of Perga posed and solved this famous problem in his work ; this work has been lost, but a 4th-century report of his results by Pappus of Alexandria has survived...
, and the three-dimensional Soddy's hexlet
Soddy's hexlet
In geometry, Soddy's hexlet is a chain of six spheres , each of which is tangent to both of its neighbors and also to three mutually tangent given spheres. In Figure 1, these three spheres are shown as an outer circumscribing sphere C , and two spheres A and B above and below the plane of their...
. Similarly, if some circles of the Steiner chain are externally tangent to both given circles, their centers must lie on a hyperbola, whereas those that are internally tangent to both lie on a different hyperbola.
The circles of the Steiner chain are tangent to two fixed circles, denoted here as α and β, where β is enclosed by α. Let the radii of these two circles be denoted as rα and rβ, respectively, and let their respective centers be the points A and B. Let the radius, diameter and center point of the kth circle of the Steiner chain be denoted as rk, dk and Pk, respectively.
All the centers of the circles in the Steiner chain are located on a common ellipse
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
, for the following reason. The sum of the distances from the kth circle of the Pappus chain to the two centers A and B of thefixed circles equals a constant

Thus, for all the centers of the circles of the Steiner chain, the sum of distances to A and B equals the same constant, rα+rβ. This defines an ellipse, whose two foci
Focus (geometry)
In geometry, the foci are a pair of special points with reference to which any of a variety of curves is constructed. For example, foci can be used in defining conic sections, the four types of which are the circle, ellipse, parabola, and hyperbola...
are the points A and B, the centers of the circles, α and β, that sandwich the Steiner chain of circles. The property of having centers on an ellipse is common to all situations where a series of circles is tangent to two fixed circles, such as the related Pappus chain
Pappus chain
In geometry, the Pappus chain was created by Pappus of Alexandria in the 3rd century AD.-Construction:The arbelos is defined by two circles, CU and CV, which are tangent at the point A and where CU is enclosed by CV...
of circles and the three-dimensional Soddy's hexlet
Soddy's hexlet
In geometry, Soddy's hexlet is a chain of six spheres , each of which is tangent to both of its neighbors and also to three mutually tangent given spheres. In Figure 1, these three spheres are shown as an outer circumscribing sphere C , and two spheres A and B above and below the plane of their...
.
The sum of distances to the foci equals twice the semi-major axis
Semi-major axis
The major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
a of an ellipse; hence,
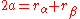
Let p equal the distance between the foci, A and B. Then, the eccentricity
Eccentricity (mathematics)
In mathematics, the eccentricity, denoted e or \varepsilon, is a parameter associated with every conic section. It can be thought of as a measure of how much the conic section deviates from being circular.In particular,...
e is defined by 2 ae = p, or
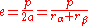
From these parameters, the semi-minor axis
Semi-minor axis
In geometry, the semi-minor axis is a line segment associated with most conic sections . One end of the segment is the center of the conic section, and it is at right angles with the semi-major axis...
b and the semi-latus rectum L can be determined
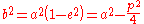
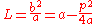
Therefore, the ellipse can be described by an equation in terms of its distance d to one focus
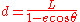
where θ is the angle with the line joining the two foci.
Conjugate chains
If a Steiner chain has an even number of circles, then any two diametrically opposite circles in the chain can be taken as the two given circles of a new Steiner chain to which the original circles belong. If the original Steiner chain has n circles in m wraps, and the new chain has p circles in q wraps, then the equation holds

A simple example occurs for Steiner chains of four circles (n = 4) and one wrap (m = 1). In this case, the given circles and the Steiner-chain circles are equivalent in that both types of circles are tangent to four others; more generally, Steiner-chain circles are tangent to four circles, but the two given circles are tangent to n circles. In this case, any pair of opposite members of the Steiner chain may be selected as the given circles of another Steiner chain that involves the original given circles. Since m = p = 1 and n = q = 4, Steiner's equation is satisfied:
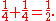
Generalizations
Pappus chain
In geometry, the Pappus chain was created by Pappus of Alexandria in the 3rd century AD.-Construction:The arbelos is defined by two circles, CU and CV, which are tangent at the point A and where CU is enclosed by CV...
, which has an infinite number of circles.
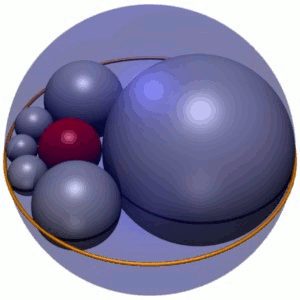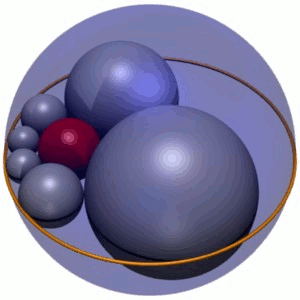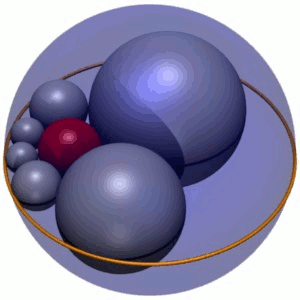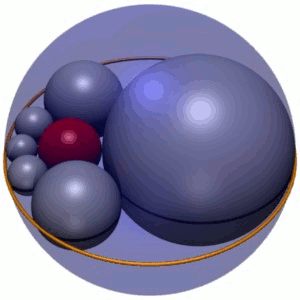
Soddy's hexlet
Soddy's hexlet
In geometry, Soddy's hexlet is a chain of six spheres , each of which is tangent to both of its neighbors and also to three mutually tangent given spheres. In Figure 1, these three spheres are shown as an outer circumscribing sphere C , and two spheres A and B above and below the plane of their...
is a three-dimensional generalization of a Steiner chain of six circles. The centers of the six spheres (the hexlet) travel along the same ellipse as do the centers of the corresponding Steiner chain. The envelope of the hexlet spheres is a Dupin cyclide, the inversion of a torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
. The six spheres are not only tangent to the inner and outer sphere, but also to two other spheres, centered above and below the plane of the hexlet centers.
Multiple rings of Steiner chains are another generalization. An ordinary Steiner chain is obtained by inverting an annular chain of tangent circles bounded by two concentric circles. This may be generalized to inverting three or more concentric circles that sandwich annular chains of tangent circles.
Hierarchical Steiner chains are yet another generalization. If the two given circles of an ordinary Steiner chain are nested, i.e., if one lies entirely within the other, then the larger given circle circumscribes the Steiner-chain circles. In a hierarchical Steiner chain, each circle of a Steiner chain is itself the circumscribing given circle of another Steiner chain within it; this process may be repeated indefinitely, forming a fractal
Fractal
A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
.
External links
- Interactive animation of a Steiner chain
- Java applet by Michael Borcherds showing an animation of Steiner's Chain with a variable number of circles made with GeoGebra.

