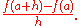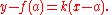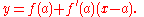Tangent
Encyclopedia

Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the tangent line (or simply the tangent) to a plane curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
at a given point
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f is the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of f. A similar definition applies to space curves and curves in n-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
.
As it passes through the point where the tangent line and the curve meet, or the point of tangency, the tangent line is "going in the same direction" as the curve, and in this sense it is the best straight-line approximation to the curve at that point.
Similarly, the tangent plane to a surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
at a given point is the plane
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
that "just touches" the surface at that point. The concept of a tangent is one of the most fundamental notions in differential geometry and has been extensively generalized; see Tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
.
The word "tangent" comes from the Latin tangens, meaning "touching".
Tangent line to a curve
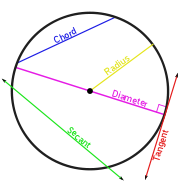
Secant line
A secant line of a curve is a line that intersects two points on the curve. The word secant comes from the Latin secare, to cut.It can be used to approximate the tangent to a curve, at some point P...
s) passing through two points, A and B, those that lie on the function curve. The tangent at A is the limit when point B approximates or tends to A. The existence and uniqueness of the tangent line depends on a certain type of mathematical smoothness, known as "differentiability." For example, if two circular arcs meet at a sharp point (a vertex) then there is no uniquely defined tangent at the vertex because the limit of the progression of secant lines depends on the direction in which "point B" approaches the vertex.
If the curvature is nonzero, the tangent to a curve does not cross the curve at the point of tangency (though it may, when continued, cross the curve at other places away from the point of tangent) This is true, for example, of all tangents to a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
or a parabola
Parabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
. However, at exceptional points called inflection point
Inflection point
In differential calculus, an inflection point, point of inflection, or inflection is a point on a curve at which the curvature or concavity changes sign. The curve changes from being concave upwards to concave downwards , or vice versa...
s, the tangent line does cross the curve at the point of tangency. An example is the point (0,0) on the graph of the cubic parabola y = x3.
Conversely, it may happen that the curve lies entirely on one side of a straight line passing through a point on it, and yet this straight line is not a tangent line. This is the case, for example, for a line passing through the vertex of a triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
and not intersecting the triangle—where the tangent line does not exist for the reasons explained above. In convex geometry
Convex geometry
Convex geometry is the branch of geometry studying convex sets, mainly in Euclidean space.Convex sets occur naturally in many areas of mathematics: computational geometry, convex analysis, discrete geometry, functional analysis, geometry of numbers, integral geometry, linear programming,...
, such lines are called supporting lines
Supporting hyperplane
Supporting hyperplane is a concept in geometry. A hyperplane divides a space into two half-spaces. A hyperplane is said to support a set S in Euclidean space \mathbb R^n if it meets both of the following:...
.
Analytical approach
The geometric idea of the tangent line as the limit of secant lines serves as the motivation for analytical methods that are used to find tangent lines explicitly. The question of finding the tangent line to a graph, or the tangent line problem, was one of the central questions leading to the development of calculusCalculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
in the 17th century. In the second book of his Geometry
La Géométrie
La Géométrie was published in 1637 as an appendix to Discours de la méthode , written by René Descartes. In the Discourse, he presents his method for obtaining clarity on any subject...
, René Descartes
René Descartes
René Descartes ; was a French philosopher and writer who spent most of his adult life in the Dutch Republic. He has been dubbed the 'Father of Modern Philosophy', and much subsequent Western philosophy is a response to his writings, which are studied closely to this day...
said of the problem of constructing the tangent to a curve, "And I dare say that this is not only the most useful and most general problem in geometry that I know, but even that I have ever desired to know".
Intuitive description
Suppose that a curve is given as the graph of a functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
, y = f(x). To find the tangent line at the point p = (a, f(a)), consider another nearby point q = (a + h, f(a + h)) on the curve. The slope
Slope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
of the secant line
Secant line
A secant line of a curve is a line that intersects two points on the curve. The word secant comes from the Latin secare, to cut.It can be used to approximate the tangent to a curve, at some point P...
passing through p and q is equal to the difference quotient
Difference quotient
The primary vehicle of calculus and other higher mathematics is the function. Its "input value" is its argument, usually a point expressible on a graph...
As the point q approaches p, which corresponds to making h smaller and smaller, the difference quotient should approach a certain limiting value k, which is the slope of the tangent line at the point p. If k is known, the equation of the tangent line can be found in the point-slope form:
More rigorous description
To make the preceding reasoning rigorous, one has to explain what is meant by the difference quotient approaching a certain limiting value k. The precise mathematical formulation was given by Cauchy in the 19th century and is based on the notion of limitLimit of a function
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
. Suppose that the graph does not have a break or a sharp edge at p and it is neither plumb nor too wiggly near p. Then there is a unique value of k such that as h approaches 0, the difference quotient gets closer and closer to k, and the distance between them becomes negligible compared with the size of h, if h is small enough. This leads to the definition of the slope of the tangent line to the graph as the limit of the difference quotients for the function f. This limit is the derivative of the function f at x = a, denoted f ′(a). Using derivatives, the equation of the tangent line can be stated as follows:
Calculus provides rules for computing the derivatives of functions that are given by formulas, such as the power function
Power function
In mathematics, a power function is a function of the form , where c and a are constant real numbers and x is a variable.Power functions are a special case of power law relationships, which appear throughout mathematics and statistics....
, trigonometric functions, exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
, logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
, and their various combinations. Thus, equations of the tangents to graphs of all these functions, as well as many others, can be found by the methods of calculus.
How the method can fail
Calculus also demonstrates that there are functions and points on their graphs for which the limit determining the slope of the tangent line does not exist. For these points the function f is non-differentiable. There are two possible reasons for the method of finding the tangents based on the limits and derivatives to fail: either the geometric tangent exists, but it is a vertical line, which cannot be given in the point-slope form since it does not have a slope, or the graph exhibits one of three behaviors that precludes a geometric tangent.The graph y = x1/3 illustrates the first possibility: here the difference quotient at a = 0 is equal to h1/3/h = h−2/3, which becomes very large as h approaches 0. The tangent line to this curve at the origin is vertical.
The graph y = |x| of the absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
function consists of two straight lines with different slopes joined at the origin. As a point q approaches the origin from the right, the secant line always has slope 1. As a point q approaches the origin from the left, the secant line always has slope −1. Therefore, there is no unique tangent to the graph at the origin. Having two different (but finite) slopes is called a corner.
A cusp
Cusp (singularity)
In the mathematical theory of singularities a cusp is a type of singular point of a curve. Cusps are local singularities in that they are not formed by self intersection points of the curve....
occurs when the slope approaches infinity. This can mean one side of the graph has a slope that approaches plus or minus infinity while the slope other is finite. It can also mean both sides' slopes approaches positive infinity or negative infinity.
Finally, since differentiability implies continuity, the contrapositive
Contraposition
In traditional logic, contraposition is a form of immediate inference in which from a given proposition another is inferred having for its subject the contradictory of the original predicate, and in some cases involving a change of quality . For its symbolic expression in modern logic see the rule...
states discontinuity implies non-differentiability. Any such jump or point discontinuity will have no tangent line. This includes cases where one slope approaches positive infinity while the other approaches negative infinity, leading to an infinite jump discontinuity
Equations
When the curve is given by y = f(x) then the slope of the tangent is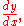
so by the point–slope formula the equation of the tangent line at (X, Y) is
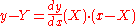
where (x, y) are the coordinates of any point on the tangent line, and where the derivative is evaluated at
 .
.When the curve is given by y = f(x), the tangent line's equation can also be found by using polynomial division to divide
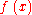 by
by  ; if the remainder is denoted by
; if the remainder is denoted by 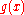 , then the equation of the tangent line is given by
, then the equation of the tangent line is given by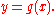
When the equation of the curve is given in the form f(x, y) = 0 then the value of the slope can be found by implicit differentiation, giving
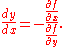
The equation of the tangent line is then
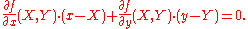
For algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
s, computations may be simplified somewhat by converting to homogeneous coordinates. Specifically, let the homogeneous equation of the curve be g(x, y, z) = 0 where g is a homogeneous function of degree n. Then, if (X, Y, Z) lies on the curve, Euler's theorem implies
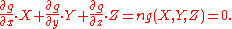
It follows that the homogeneous equation of the tangent line is
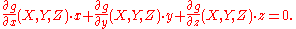
The equation of the tangent line in Cartesian coordinates can be found by setting z=1 in this equation.
To apply this to algebraic curves, write f(x, y) as
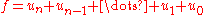
where each ur is the sum of all terms of degree r. The homogeneous equation of the curve is then

Applying the equation above and setting z=1 produces
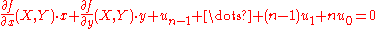
as the equation of the tangent line. The equation in this form is often simpler to use in practice since no further simplification is needed after it is applied.
If the curve is given parametrically
Parametric equation
In mathematics, parametric equation is a method of defining a relation using parameters. A simple kinematic example is when one uses a time parameter to determine the position, velocity, and other information about a body in motion....
by
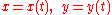
then the slope of the tangent is

giving the equation for the tangent line at
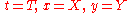 as
as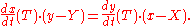
Normal line to a curve
The line perpendicular to the tangent line to a curve at the point of tangency is called the normal line to the curve at that point. The slopes of perpendicular lines have product −1, so if the equation of the curve is y = f(x) then slope of the normal line is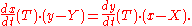
and it follows that the equation of the normal line is

Similarly, if the equation of the curve has the form f(x, y) = 0 then the equation of the tangent line is given by
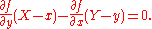
If the curve is given parametrically by
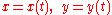
then the equation of the normal line is
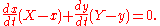
Angle between curves
The angle between two curves at a point where they intersect is defined as the angle between their tangent lines at that point. More specifically, two curves are said to be tangent at a point if they have the same tangent at a point, and orthogonal if their tangent lines are orthogonal.Multiple tangents at the origin

Singular point of a curve
In geometry, a singular point on a curve is one where the curve is not given by a smooth embedding of a parameter. The precise definition of a singular point depends on the type of curve being studied.-Algebraic curves in the plane:...
. In this case there may be two or more branches of the curve which pass through the point, each branch having its own tangent line. When the point is the origin, the equations of these lines can be found for algebraic curves by factoring the equation formed by eliminating all but the lowest degree terms from the original equation. Since any point can be made the origin by a change of variables, this gives a method for finding the tangent lines at any singular point.
For example, the equation of the limaçon trisectrix
Limaçon trisectrix
In geometry, a limaçon trisectrix is a member of the Limaçon family of curves which has the trisectrix, or angle trisection, property...
shown to the right is
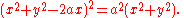
Expanding this and eliminating all but terms of degree 2 gives
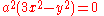
which, when factored, becomes

So these are the equations of the two tangent lines through the origin.
Tangent circles
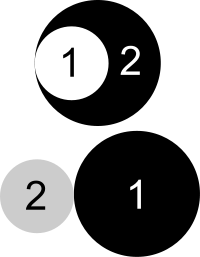
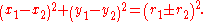
- Two circles are externally tangent if the distance between their centres is equal to the sum of their radii.

- Two circles are internally tangent if the distance between their centres is equal to the difference between their radii.
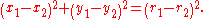
Surfaces and higher-dimensional manifolds
The tangent plane to a surfaceSurface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
at a given point p is defined in an analogous way to the tangent line in the case of curves. It is the best approximation of the surface by a plane at p, and can be obtained as the limiting position of the planes passing through 3 distinct points on the surface close to p as these points converge to p. More generally, there is a k-dimensional tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
at each point of a k-dimensional manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
in the n-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
.
See also
- Newton's methodNewton's methodIn numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
- Surface normalSurface normalA surface normal, or simply normal, to a flat surface is a vector that is perpendicular to that surface. A normal to a non-flat surface at a point P on the surface is a vector perpendicular to the tangent plane to that surface at P. The word "normal" is also used as an adjective: a line normal to a...
- Osculating circleOsculating circleIn differential geometry of curves, the osculating circle of a sufficiently smooth plane curve at a given point p on the curve has been traditionally defined as the circle passing through p and a pair of additional points on the curve infinitesimally close to p...
- Osculating curveOsculating curveIn mathematics and geometry, an osculating curve is an extension of the concept of tangent. A tangent line to a curve is the straight line that shares the location and direction of the curve, while an osculating circle to the same curve shares the location, direction, and curvature.Two curves are...
- SubtangentSubtangentIn geometry, the subtangent and related terms are certain line segments defined using the line tangent to a curve at a given point and the coordinate axes...
- Tangent coneTangent coneIn geometry, the tangent cone is a generalization of the notion of the tangent space to a manifold to the case of certain spaces with singularities.- Definition in convex geometry :...
- Tangential angleTangential angleIn geometry, the tangential angle of a curve in the Cartesian plane, at a specific point, is the angle between the tangent line to the curve at the given point and the x-axis. In geometry, the tangential angle of a curve in the Cartesian plane, at a specific point, is the angle between the tangent...
- Tangential componentTangential and normal componentsIn mathematics, given a vector at a point on a curve, that vector can be decomposed uniquely as a sum of two vectors, one tangent to the curve, called the tangential component of the vector, and another one perpendicular to the curve, called the normal component of the vector...
- Tangent lines to circlesTangent lines to circlesIn Euclidean plane geometry, tangent lines to circles form the subject of several theorems, and play an important role in many geometrical constructions and proofs...
- PerpendicularPerpendicularIn geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
- Supporting lineSupporting lineIn geometry, a supporting line L of a curve C in the plane is a line that contains a point of C, but does not separate any two points of C. In other words, C lies completely in one of the two closed half-planes defined by L and has at least one point on L.There can be many supporting lines for a...
External links
- Tangent to a circle With interactive animation
- Tangent and first derivative - An interactive simulation
- The Tangent Parabola by John H. Mathews