Bipolar coordinates
Encyclopedia
Bipolar coordinates are a two-dimensional orthogonal
coordinate system
. There are two commonly defined types of bipolar coordinates. The other system is two-center bipolar coordinates
. There is also a third coordinate system that is based on two poles (biangular coordinates). The first is based on the Apollonian circles
. The curves of constant σ and of τ are circles that intersect at right angles. The coordinates have two foci
F1 and F2, which are generally taken to be fixed at (−a, 0) and (a, 0), respectively, on the x-axis of a Cartesian coordinate system
.
Bipolar coordinates form the basis for several sets of three-dimensional orthogonal coordinates
. The bipolar cylindrical coordinates
are produced by projecting in the z-direction. The bispherical coordinates
are produced by rotating the bipolar coordinates about the
-axis, i.e., the axis connecting the foci, whereas the toroidal coordinates
are produced by rotating the bipolar coordinates about the y-axis, i.e., the axis separating the foci.
The classic applications of bipolar coordinates are in solving partial differential equations, e.g., Laplace's equation
or the Helmholtz equation
, for which bipolar coordinates allow a separation of variables
. A typical example would be the electric field
surrounding two parallel cylindrical conductors.
The term "bipolar" is sometimes used to describe other curves having two singular points (foci), such as ellipse
s, hyperbola
s, and Cassini oval
s. However, the term bipolar coordinates is reserved for the coordinates described here, and never used to describe coordinates associated with those other curves, such as elliptic coordinates
.
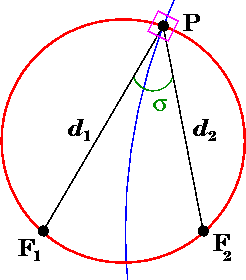
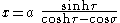
where the σ-coordinate of a point P equals the angle F1 P F2 and the τ-coordinate equals the natural logarithm
of the ratio of the distances d1 and d2 to the foci
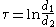
(Recall that F1 and F2 are located at (−a, 0) and (a, 0), respectively.)
The σ and τ isosurfaces intersect at two points, not one. The foci divide each σ-isosurface circle into a longer and shorter arc. By convention, the σ on these two arcs differ by 90°, i.e., σshorter = σlonger + 90°; this convention breaks the degeneracy of the coordinate system.
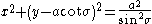
that intersect at the two foci. The centers of the constant-σ circles lie on the y-axis. Circles of positive σ are centered above the x-axis, whereas those of negative σ lie below the axis. As the magnitude |σ| increases, the radius of the circles decreases and the center approaches the origin (0, 0), which is reached when |σ| = π/2, its maximum value.
The curves of constant
are non-intersecting circles of different radii
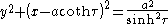
that surround the foci but again are not concentric. The centers of the constant-τ circles lie on the x-axis. The circles of positive τ lie in the right-hand side of the plane (x > 0), whereas the circles of negative τ lie in the left-hand side of the plane (x < 0). The τ = 0 curve corresponds to the y-axis (x = 0). As the magnitude of τ increases, the radius of the circles decreases and their centers approach the foci.
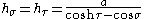
Thus, the infinitesimal area element equals
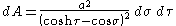
and the Laplacian is given by
Other differential operators such as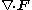
and 
can be expressed in the coordinates (σ, τ) by substituting the scale factors into the general formulae found in orthogonal coordinates
.
Orthogonal coordinates
In mathematics, orthogonal coordinates are defined as a set of d coordinates q = in which the coordinate surfaces all meet at right angles . A coordinate surface for a particular coordinate qk is the curve, surface, or hypersurface on which qk is a constant...
coordinate system
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
. There are two commonly defined types of bipolar coordinates. The other system is two-center bipolar coordinates
Two-center bipolar coordinates
In mathematics, two-center bipolar coordinates is a coordinate system, based on two coordinates which give distances from two fixed centers, C1 and C2 This system is very useful in some scientific applications It should not be confused with so-called bipolar coordinates.-Cartesian...
. There is also a third coordinate system that is based on two poles (biangular coordinates). The first is based on the Apollonian circles
Apollonian circles
Apollonian circles are two families of circles such that every circle in the first family intersects every circle in the second family orthogonally, and vice versa. These circles form the basis for bipolar coordinates...
. The curves of constant σ and of τ are circles that intersect at right angles. The coordinates have two foci
Focus (geometry)
In geometry, the foci are a pair of special points with reference to which any of a variety of curves is constructed. For example, foci can be used in defining conic sections, the four types of which are the circle, ellipse, parabola, and hyperbola...
F1 and F2, which are generally taken to be fixed at (−a, 0) and (a, 0), respectively, on the x-axis of a Cartesian coordinate system
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
.
Bipolar coordinates form the basis for several sets of three-dimensional orthogonal coordinates
Orthogonal coordinates
In mathematics, orthogonal coordinates are defined as a set of d coordinates q = in which the coordinate surfaces all meet at right angles . A coordinate surface for a particular coordinate qk is the curve, surface, or hypersurface on which qk is a constant...
. The bipolar cylindrical coordinates
Bipolar cylindrical coordinates
Bipolar cylindrical coordinates are a three-dimensional orthogonal coordinate system that results from projecting the two-dimensional bipolar coordinate system in theperpendicular z-direction...
are produced by projecting in the z-direction. The bispherical coordinates
Bispherical coordinates
Bispherical coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional bipolar coordinate system about the axis that connects the two foci...
are produced by rotating the bipolar coordinates about the
-axis, i.e., the axis connecting the foci, whereas the toroidal coordinatesToroidal coordinates
Toroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional bipolar coordinate system about the axis that separates its two foci. Thus, the two foci F_1 and F_2 in bipolar coordinates become a ring of radius a in the xy plane of the...
are produced by rotating the bipolar coordinates about the y-axis, i.e., the axis separating the foci.
The classic applications of bipolar coordinates are in solving partial differential equations, e.g., Laplace's equation
Laplace's equation
In mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as:where ∆ = ∇² is the Laplace operator and \varphi is a scalar function...
or the Helmholtz equation
Helmholtz equation
The Helmholtz equation, named for Hermann von Helmholtz, is the elliptic partial differential equation\nabla^2 A + k^2 A = 0where ∇2 is the Laplacian, k is the wavenumber, and A is the amplitude.-Motivation and uses:...
, for which bipolar coordinates allow a separation of variables
Separation of variables
In mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation....
. A typical example would be the electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
surrounding two parallel cylindrical conductors.
The term "bipolar" is sometimes used to describe other curves having two singular points (foci), such as ellipse
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
s, hyperbola
Hyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
s, and Cassini oval
Cassini oval
A Cassini oval is a plane curve defined as the set of points in the plane such that the product of the distances to two fixed points is constant. This is related to an ellipse, for which the...
s. However, the term bipolar coordinates is reserved for the coordinates described here, and never used to describe coordinates associated with those other curves, such as elliptic coordinates
Elliptic coordinates
In geometry, the elliptic coordinate system is a two-dimensional orthogonal coordinate system in whichthe coordinate lines are confocal ellipses and hyperbolae...
.
Basic definition
The most common definition of bipolar coordinates (σ, τ) is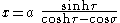where the σ-coordinate of a point P equals the angle F1 P F2 and the τ-coordinate equals the natural logarithm
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
of the ratio of the distances d1 and d2 to the foci
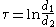
(Recall that F1 and F2 are located at (−a, 0) and (a, 0), respectively.)
The σ and τ isosurfaces intersect at two points, not one. The foci divide each σ-isosurface circle into a longer and shorter arc. By convention, the σ on these two arcs differ by 90°, i.e., σshorter = σlonger + 90°; this convention breaks the degeneracy of the coordinate system.
Curves of constant σ and τ
The curves of constant σ correspond to non-concentric circles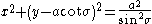that intersect at the two foci. The centers of the constant-σ circles lie on the y-axis. Circles of positive σ are centered above the x-axis, whereas those of negative σ lie below the axis. As the magnitude |σ| increases, the radius of the circles decreases and the center approaches the origin (0, 0), which is reached when |σ| = π/2, its maximum value.
The curves of constant
are non-intersecting circles of different radii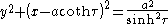that surround the foci but again are not concentric. The centers of the constant-τ circles lie on the x-axis. The circles of positive τ lie in the right-hand side of the plane (x > 0), whereas the circles of negative τ lie in the left-hand side of the plane (x < 0). The τ = 0 curve corresponds to the y-axis (x = 0). As the magnitude of τ increases, the radius of the circles decreases and their centers approach the foci.
Scale factors
The scale factors for the bipolar coordinates (σ, τ) are equal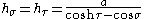Thus, the infinitesimal area element equals
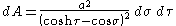
and the Laplacian is given by
Other differential operators such as
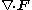and can be expressed in the coordinates (σ, τ) by substituting the scale factors into the general formulae found in orthogonal coordinatesOrthogonal coordinates
In mathematics, orthogonal coordinates are defined as a set of d coordinates q = in which the coordinate surfaces all meet at right angles . A coordinate surface for a particular coordinate qk is the curve, surface, or hypersurface on which qk is a constant...
.