Locally integrable function
Encyclopedia
In mathematics
, a locally integrable function is a function
which is integrable on any compact set of its domain of definition. Their importance lies on the fact that we do not care about their behavior at infinity.
be an open set
in the Euclidean space
ℝn and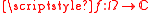
be a Lebesgue
measurable function
. If the Lebesgue integral of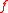
is such that
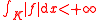
i.e. it is finite for all compact subsets
in 
, then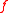 
is called locally integrable. The set of all such functions is denoted by 
:
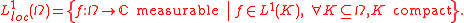
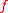belonging to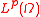 
,
, where 
is an open subset of ℝn is locally integrable.
To see this, consider the characteristic function
of a compact subset 
of 
: then, for 
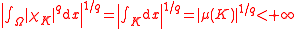
where
Then by Hölder's inequality
, the product
is integrable i.e. belongs to 
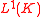and
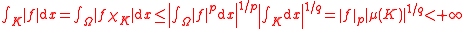
therefore
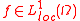
Note that since the following inequality is true
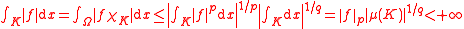
the theorem is true also for functions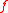
belonging only to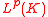 
for each compact subset
of 
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a locally integrable function is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
which is integrable on any compact set of its domain of definition. Their importance lies on the fact that we do not care about their behavior at infinity.
Formal definition
Formally, let be an open setOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
in the Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
ℝn and
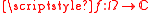be a LebesgueLebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
measurable function
Measurable function
In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
. If the Lebesgue integral of
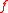is such that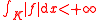i.e. it is finite for all compact subsets
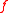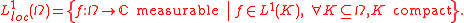
in , then is called locally integrable. The set of all such functions is denoted by :Properties
Theorem. Every function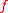 belonging to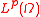 Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
,
, where is an open subset of ℝn is locally integrable.To see this, consider the characteristic function
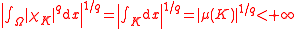
of a compact subset of : then, for where
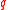is the positive number such that 
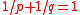for a given 
is the Lebesgue measureLebesgue measureIn measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
of the compact set
Then by Hölder's inequality
Hölder's inequality
In mathematical analysis Hölder's inequality, named after Otto Hölder, is a fundamental inequality between integrals and an indispensable tool for the study of Lp spaces....
, the product
Product (mathematics)
In mathematics, a product is the result of multiplying, or an expression that identifies factors to be multiplied. The order in which real or complex numbers are multiplied has no bearing on the product; this is known as the commutative law of multiplication...
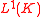is integrable i.e. belongs to and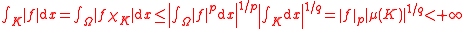therefore
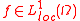
Note that since the following inequality is true
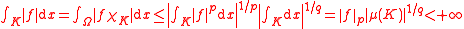
the theorem is true also for functions
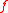belonging only to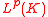 Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
for each compact subset
of .Examples
- The constant function
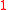defined on the real line is locally integrable but not globally integrable. More generally, continuous functionContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s and constants are locally integrable. - The function
- is not locally integrable near
.
Applications
Locally integrable functions play a prominent role in distribution theoryDistribution (mathematics)In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
. Also they occur in the definition of various classes of functionsFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
and function spaceFunction spaceIn mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
s, like functions of bounded variationBounded variationIn mathematical analysis, a function of bounded variation, also known as a BV function, is a real-valued function whose total variation is bounded : the graph of a function having this property is well behaved in a precise sense...
.
See also
- Compact set
- Distribution (mathematics)Distribution (mathematics)In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
- Lebesgue integral
- Lebesgue measureLebesgue measureIn measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
- Lp(Ω) spaceLp spaceIn mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
- is not locally integrable near