Convergence in measure
Encyclopedia
Convergence in measure can refer to two distinct mathematical concepts which both generalize
the concept of convergence in probability.
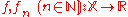 be measurable functions on a measure space (X,Σ,μ). The sequence (fn) is said
be measurable functions on a measure space (X,Σ,μ). The sequence (fn) is said
to converge globally in measure to f if for every ε > 0,
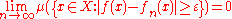 ,
,
and to converge locally in measure to f if for every ε > 0 and every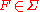 with
with
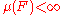 ,
,
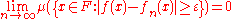 .
.
Convergence in measure can refer to either global convergence in measure or local convergence in measure, depending on the author.
 N) are measurable functions X → R.
N) are measurable functions X → R.
 , μ be Lebesgue measure, and f the constant function with value zero.
, μ be Lebesgue measure, and f the constant function with value zero.
(The first five terms of which are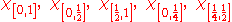 )
)
converges to f locally in measure; but for no x does fn(x) converge to zero.
Hence (fn) fails to converge to f almost everywhere.
, called the topology of (local) convergence in measure, on the collection of measurable functions from X such that local convergence in measure corresponds to convergence on that topology.
This topology is defined by the family of pseudometrics
where
Because this topology is generated by a family of pseudometrics, it is uniformizable
.
Working with uniform structures instead of topologies allows us to formulate uniform properties such as
Cauchyness.
the concept of convergence in probability.
Definitions
Let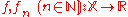 be measurable functions on a measure space (X,Σ,μ). The sequence (fn) is said
be measurable functions on a measure space (X,Σ,μ). The sequence (fn) is saidto converge globally in measure to f if for every ε > 0,
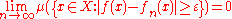 ,
,and to converge locally in measure to f if for every ε > 0 and every
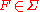 with
with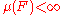 ,
,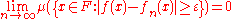 .
.Convergence in measure can refer to either global convergence in measure or local convergence in measure, depending on the author.
Properties
Throughout, f and fn (n N) are measurable functions X → R.
N) are measurable functions X → R.- Global convergence in measure implies local convergence in measure. The converse, however, is false; i.e., local convergence in measure is strictly weaker than global convergence in measure, in general.
- If, however,
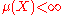 or, more generally, if all the fn vanish outside some set of finite measure, then the distinction between local and global convergence in measure disappears.
or, more generally, if all the fn vanish outside some set of finite measure, then the distinction between local and global convergence in measure disappears.
- If μ is σ-finite and (fn) converges (locally or globally) to f in measure, there is a subsequence converging to f almost everywhereAlmost everywhereIn measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
.
- If μ is σ-finite, (fn) converges to f locally in measure if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
every subsequence has in turn a subsequence that converges to f almost everywhere.
- In particular, if (fn) converges to f almost everywhere, then (fn) converges to f locally in measure. The converse is false.
- Fatou's lemmaFatou's lemmaIn mathematics, Fatou's lemma establishes an inequality relating the integral of the limit inferior of a sequence of functions to the limit inferior of integrals of these functions...
and the monotone convergence theorem hold if almost everywhere convergence is replaced by (local or global) convergence in measure.
- If μ is σ-finite, Lebesgue's dominated convergence theoremDominated convergence theoremIn measure theory, Lebesgue's dominated convergence theorem provides sufficient conditions under which two limit processes commute, namely Lebesgue integration and almost everywhere convergence of a sequence of functions...
also holds if almost everywhere convergence is replaced by (local or global) convergence in measure.
- If X = [a,b] ⊆ R and μ is Lebesgue measureLebesgue measureIn measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
, there are sequences (gn) of step functions and (hn) of continuous functions converging globally in measure to f.
- If f and fn (n ∈ N) are in Lp(μ)Lp spaceIn mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
for some p > 0 and (fn) converges to f in the p-norm, then (fn) converges to f globally in measure. The converse is false.
- If fn converges to f in measure and gn converges to g in measure then fn + gn converges to f + g in measure. Additionally, if the measure space is finite, fngn also converges to fg.
Counterexamples
Let , μ be Lebesgue measure, and f the constant function with value zero.
, μ be Lebesgue measure, and f the constant function with value zero.- The sequence
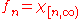 converges to f locally in measure, but does not converge to f globally in measure.
converges to f locally in measure, but does not converge to f globally in measure.
- The sequence
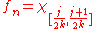 where
where 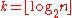 and
and 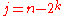
(The first five terms of which are
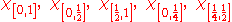 )
)converges to f locally in measure; but for no x does fn(x) converge to zero.
Hence (fn) fails to converge to f almost everywhere.
- The sequence
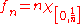 converges to f almost everywhere (hence also locally in measure), but not in the p-norm for any
converges to f almost everywhere (hence also locally in measure), but not in the p-norm for any  .
.
Topology
There is a topologyTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
, called the topology of (local) convergence in measure, on the collection of measurable functions from X such that local convergence in measure corresponds to convergence on that topology.
This topology is defined by the family of pseudometrics
Pseudometric space
In mathematics, a pseudometric space is a generalized metric space in which the distance between two distinct points can be zero. In the same way as every normed space is a metric space, every seminormed space is a pseudometric space...
where
-
 .
.
Because this topology is generated by a family of pseudometrics, it is uniformizable
Uniform space
In the mathematical field of topology, a uniform space is a set with a uniform structure. Uniform spaces are topological spaces with additional structure which is used to define uniform properties such as completeness, uniform continuity and uniform convergence.The conceptual difference between...
.
Working with uniform structures instead of topologies allows us to formulate uniform properties such as
Cauchyness.