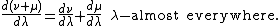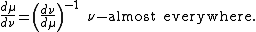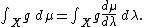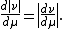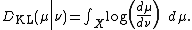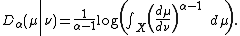Radon–Nikodym theorem
Encyclopedia
In mathematics
, the Radon–Nikodym theorem is a result in measure theory that states that, given a measurable space
(X,Σ), if a σ-finite measure ν on (X,Σ) is absolutely continuous with respect to a σ-finite measure μ on (X,Σ), then there is a measurable function
f on X and taking values in [0,∞), such that
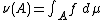
for any measurable set A.
The theorem is named after Johann Radon
, who proved the theorem for the special case where the underlying space is RN in 1913, and for Otto Nikodym who proved the general case in 1930.
If Y is a Banach space
and the generalization of the Radon–Nikodym theorem also holds for functions with values in Y (mutatis mutandis
), then Y is said to have the Radon–Nikodym property. All Hilbert space
s have the Radon–Nikodym property.
a μ-null set
, that is, if g is another function which satisfies the same property, then f = g μ-almost everywhere
. f is commonly written dν/dμ and is called the Radon–Nikodym derivative. The choice of notation and the name of the function reflects the fact that the function is analogous to a derivative
in calculus
in the sense that it describes the rate of change of density of one measure with respect to another (the way the Jacobian determinant is used in multivariable integration). A similar theorem can be proven for signed
and complex measure
s: namely, that if μ is a nonnegative σ-finite measure, and ν is a finite-valued signed or complex measure such that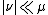 , there is μ-integrable real- or complex-valued function g on X such that
, there is μ-integrable real- or complex-valued function g on X such that
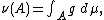
for any measurable set A.
from probability masses and probability densities defined over real numbers to probability measure
s defined over arbitrary sets. It tells if and how it is possible to change from one probability measure to another. Specifically, the probability density function
of a random variable
is the Radon–Nikodym derivative of the induced measure with respect to some base measure (usually the Lebesgue measure
for continuous random variables).
For example, it can be used to prove the existence of conditional expectation
for probability measures. The latter itself is a key concept in probability theory
, as conditional probability
is just a special case of it.
Amongst other fields, financial mathematics uses the theorem extensively. Such changes of probability measure are the cornerstone of the rational pricing
of derivative securities and are used for converting actual probabilities into those of the risk neutral probabilities
.
Consider the Borel sigma-algebra
on the real line
. Let the counting measure
, μ, of a Borel set A be defined as the number of elements of A if A is finite, and +∞ otherwise. One can check that μ is indeed a measure. It is not sigma-finite, as not every Borel set is at most a countable union of finite sets. Let ν be the usual Lebesgue measure
on this Borel algebra. Then, ν is absolutely continuous with respect to μ, since for a set A one has μ(A) = 0 only if A is the empty set
, and then ν(A) is also zero.
Assume that the Radon–Nikodym theorem holds, that is, for some measurable function f one has
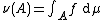
for all Borel sets. Taking A to be a singleton set, A = {a}, and using the above equality, one finds
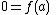
for all real numbers a. This implies that the function f, and therefore the Lebesgue measure ν, is zero, which is a contradiction.
For finite measures μ and ν, the idea is to consider functions f with f dμ ≤ dν. The supremum of all such functions, along with the monotone convergence theorem, then furnishes the Radon–Nikodym derivative. The fact that the remaining part of μ is singular with respect to ν follows from a technical fact about finite measures. Once the result is established for finite measures, extending to σ-finite, signed, and complex measures can be done naturally. The details are given below.
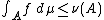
for every A ∈ Σ (this set is not empty, for it contains at least the zero function). Let f1, f2 ∈ F; let A be an arbitrary measurable set, A1 = {x ∈ A | f1(x) > f2(x)}, and A2 = {x ∈ A | f2(x) ≥ f1(x)}. Then one has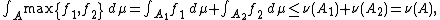
and therefore, max{f1, f2} ∈ F.
Now, let {fn}n be a sequence of functions in F such that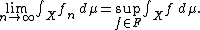
By replacing fn with the maximum of the first n functions, one can assume that the sequence {fn} is increasing. Let g be a function defined as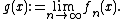
By Lebesgue's monotone convergence theorem, one has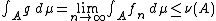
for each A ∈ Σ, and hence, g ∈ F. Also, by the construction of g,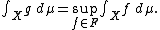
Now, since g ∈ F,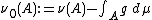
defines a nonnegative measure on Σ. Suppose ν0 ≠ 0; then, since μ is finite, there is an ε > 0 such that ν0(X) > ε μ(X). Let (P, N) be a Hahn decomposition
for the signed measure ν0 − ε μ. Note that for every A ∈ Σ one has ν0(A ∩ P) ≥ ε μ(A ∩ P), and hence,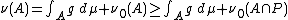
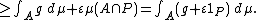
Also, note that μ(P) > 0; for if μ(P) = 0, then (since ν is absolutely continuous in relation to μ) ν0(P) ≤ ν(P) = 0, so ν0(P) = 0 and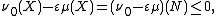
contradicting the fact that ν0(X) > ε μ(X).
Then, since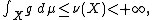
g + ε 1P ∈ F and satisfies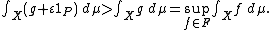
This is impossible
, therefore, the initial assumption that ν0 ≠ 0 must be false. So ν0 = 0, as desired.
Now, since g is μ-integrable, the set {x ∈ X | g(x) = +∞} is μ-null
. Therefore, if a f is defined as
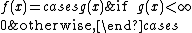
then f has the desired properties.
As for the uniqueness, let f, g : X → [0, +∞) be measurable functions satisfying
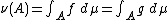
for every measurable set A. Then, g − f is μ-integrable, and
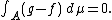
In particular, for A = {x∈X | f(x) > g(x)}, or {x ∈ X | f(x) < g(x)}. It follows that
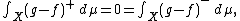
and so, that (g−f)+ = 0 μ-almost everywhere; the same is true for (g − f)−, and thus, f = g μ-almost everywhere, as desired.
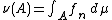
for each Σ-measurable subset A of Bn. The union
f of those functions is then the required function.
As for the uniqueness, since each of the fn is μ-almost everywhere unique, then so is f.
If ν is a complex measure
, it can be decomposed as ν = ν1 + iν2, where both ν1 and ν2 are finite-valued signed measures. Applying the above argument, one obtains two functions, g, h : X → [0, +∞), satisfying the required properties for ν1 and ν2, respectively. Clearly, f = g + i h is the required function.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Radon–Nikodym theorem is a result in measure theory that states that, given a measurable space
Sigma-algebra
In mathematics, a σ-algebra is a technical concept for a collection of sets satisfying certain properties. The main use of σ-algebras is in the definition of measures; specifically, the collection of sets over which a measure is defined is a σ-algebra...
(X,Σ), if a σ-finite measure ν on (X,Σ) is absolutely continuous with respect to a σ-finite measure μ on (X,Σ), then there is a measurable function
Measurable function
In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
f on X and taking values in [0,∞), such that
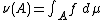
for any measurable set A.
The theorem is named after Johann Radon
Johann Radon
Johann Karl August Radon was an Austrian mathematician. His doctoral dissertation was on calculus of variations .- Life :...
, who proved the theorem for the special case where the underlying space is RN in 1913, and for Otto Nikodym who proved the general case in 1930.
If Y is a Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
and the generalization of the Radon–Nikodym theorem also holds for functions with values in Y (mutatis mutandis
Mutatis mutandis
Mutatis mutandis is a Latin phrase meaning "by changing those things which need to be changed" or more simply "the necessary changes having been made"....
), then Y is said to have the Radon–Nikodym property. All Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s have the Radon–Nikodym property.
Radon–Nikodym derivative
The function f satisfying the above equality is uniquely defined up toUp to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
a μ-null set
Null set
In mathematics, a null set is a set that is negligible in some sense. For different applications, the meaning of "negligible" varies. In measure theory, any set of measure 0 is called a null set...
, that is, if g is another function which satisfies the same property, then f = g μ-almost everywhere
Almost everywhere
In measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
. f is commonly written dν/dμ and is called the Radon–Nikodym derivative. The choice of notation and the name of the function reflects the fact that the function is analogous to a derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
in calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
in the sense that it describes the rate of change of density of one measure with respect to another (the way the Jacobian determinant is used in multivariable integration). A similar theorem can be proven for signed
Signed measure
In mathematics, signed measure is a generalization of the concept of measure by allowing it to have negative values. Some authors may call it a charge, by analogy with electric charge, which is a familiar distribution that takes on positive and negative values.-Definition:There are two slightly...
and complex measure
Complex measure
In mathematics, specifically measure theory, a complex measure generalizes the concept of measure by letting it have complex values. In other words, one allows for sets whose size is a complex number.-Definition:...
s: namely, that if μ is a nonnegative σ-finite measure, and ν is a finite-valued signed or complex measure such that
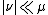 , there is μ-integrable real- or complex-valued function g on X such that
, there is μ-integrable real- or complex-valued function g on X such that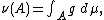
for any measurable set A.
Applications
The theorem is very important in extending the ideas of probability theoryProbability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
from probability masses and probability densities defined over real numbers to probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
s defined over arbitrary sets. It tells if and how it is possible to change from one probability measure to another. Specifically, the probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
of a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
is the Radon–Nikodym derivative of the induced measure with respect to some base measure (usually the Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
for continuous random variables).
For example, it can be used to prove the existence of conditional expectation
Conditional expectation
In probability theory, a conditional expectation is the expected value of a real random variable with respect to a conditional probability distribution....
for probability measures. The latter itself is a key concept in probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, as conditional probability
Conditional probability
In probability theory, the "conditional probability of A given B" is the probability of A if B is known to occur. It is commonly notated P, and sometimes P_B. P can be visualised as the probability of event A when the sample space is restricted to event B...
is just a special case of it.
Amongst other fields, financial mathematics uses the theorem extensively. Such changes of probability measure are the cornerstone of the rational pricing
Rational pricing
Rational pricing is the assumption in financial economics that asset prices will reflect the arbitrage-free price of the asset as any deviation from this price will be "arbitraged away"...
of derivative securities and are used for converting actual probabilities into those of the risk neutral probabilities
Risk-neutral measure
In mathematical finance, a risk-neutral measure, is a prototypical case of an equivalent martingale measure. It is heavily used in the pricing of financial derivatives due to the fundamental theorem of asset pricing, which implies that in a complete market a derivative's price is the discounted...
.
Properties
- Let ν, μ, and λ be σ-finite measures on the same measure space. If ν ≪ λ and μ ≪ λ (ν and μ are absolutely continuous in respect to λ), then
- If ν ≪ μ ≪ λ, then
- In particular, if μ ≪ ν and ν ≪ μ, then
- If μ ≪ λ and g is a μ-integrable function, then
- If ν is a finite signed or complex measure, then
Information divergences
If μ and ν are measures over X, and ν ≪ μ- The Kullback–Leibler divergenceKullback–Leibler divergenceIn probability theory and information theory, the Kullback–Leibler divergence is a non-symmetric measure of the difference between two probability distributions P and Q...
from μ to ν is defined to be
- For
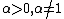 the Rényi divergence of order α from μ to ν is defined to be
the Rényi divergence of order α from μ to ν is defined to be
The assumption of σ-finiteness
The Radon–Nikodym theorem makes the assumption that the measure μ with respect to which one computes the rate of change of ν is sigma-finite. Here is an example when μ is not sigma-finite and the Radon–Nikodym theorem fails to hold.Consider the Borel sigma-algebra
Borel algebra
In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
on the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
. Let the counting measure
Counting measure
In mathematics, the counting measure is an intuitive way to put a measure on any set: the "size" of a subset is taken to be the number of elements in the subset, if the subset is finite, and ∞ if the subset is infinite....
, μ, of a Borel set A be defined as the number of elements of A if A is finite, and +∞ otherwise. One can check that μ is indeed a measure. It is not sigma-finite, as not every Borel set is at most a countable union of finite sets. Let ν be the usual Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
on this Borel algebra. Then, ν is absolutely continuous with respect to μ, since for a set A one has μ(A) = 0 only if A is the empty set
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
, and then ν(A) is also zero.
Assume that the Radon–Nikodym theorem holds, that is, for some measurable function f one has
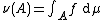
for all Borel sets. Taking A to be a singleton set, A = {a}, and using the above equality, one finds
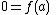
for all real numbers a. This implies that the function f, and therefore the Lebesgue measure ν, is zero, which is a contradiction.
Proof
This section gives a measure-theoretic proof of the theorem. There is also a functional-analytic proof, using Hilbert space methods, that was first given by von Neumann.For finite measures μ and ν, the idea is to consider functions f with f dμ ≤ dν. The supremum of all such functions, along with the monotone convergence theorem, then furnishes the Radon–Nikodym derivative. The fact that the remaining part of μ is singular with respect to ν follows from a technical fact about finite measures. Once the result is established for finite measures, extending to σ-finite, signed, and complex measures can be done naturally. The details are given below.
For finite measures
First, suppose that μ and ν are both finite-valued nonnegative measures. Let F be the set of those measurable functions f : X → [0, +∞] satisfying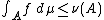
for every A ∈ Σ (this set is not empty, for it contains at least the zero function). Let f1, f2 ∈ F; let A be an arbitrary measurable set, A1 = {x ∈ A | f1(x) > f2(x)}, and A2 = {x ∈ A | f2(x) ≥ f1(x)}. Then one has
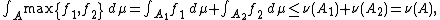
and therefore, max{f1, f2} ∈ F.
Now, let {fn}n be a sequence of functions in F such that
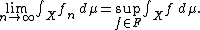
By replacing fn with the maximum of the first n functions, one can assume that the sequence {fn} is increasing. Let g be a function defined as
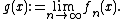
By Lebesgue's monotone convergence theorem, one has
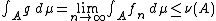
for each A ∈ Σ, and hence, g ∈ F. Also, by the construction of g,
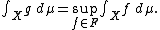
Now, since g ∈ F,
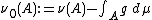
defines a nonnegative measure on Σ. Suppose ν0 ≠ 0; then, since μ is finite, there is an ε > 0 such that ν0(X) > ε μ(X). Let (P, N) be a Hahn decomposition
Hahn decomposition theorem
In mathematics, the Hahn decomposition theorem, named after the Austrian mathematician Hans Hahn, states that given a measurable space and a signed measure μ defined on the σ-algebra Σ, there exist two sets P and N in Σ such that:...
for the signed measure ν0 − ε μ. Note that for every A ∈ Σ one has ν0(A ∩ P) ≥ ε μ(A ∩ P), and hence,
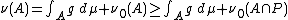
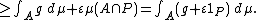
Also, note that μ(P) > 0; for if μ(P) = 0, then (since ν is absolutely continuous in relation to μ) ν0(P) ≤ ν(P) = 0, so ν0(P) = 0 and
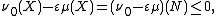
contradicting the fact that ν0(X) > ε μ(X).
Then, since
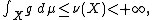
g + ε 1P ∈ F and satisfies
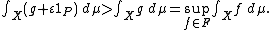
This is impossible
Reductio ad absurdum
In logic, proof by contradiction is a form of proof that establishes the truth or validity of a proposition by showing that the proposition's being false would imply a contradiction...
, therefore, the initial assumption that ν0 ≠ 0 must be false. So ν0 = 0, as desired.
Now, since g is μ-integrable, the set {x ∈ X | g(x) = +∞} is μ-null
Null set
In mathematics, a null set is a set that is negligible in some sense. For different applications, the meaning of "negligible" varies. In measure theory, any set of measure 0 is called a null set...
. Therefore, if a f is defined as
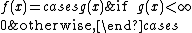
then f has the desired properties.
As for the uniqueness, let f, g : X → [0, +∞) be measurable functions satisfying
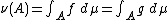
for every measurable set A. Then, g − f is μ-integrable, and
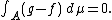
In particular, for A = {x∈X | f(x) > g(x)}, or {x ∈ X | f(x) < g(x)}. It follows that
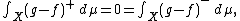
and so, that (g−f)+ = 0 μ-almost everywhere; the same is true for (g − f)−, and thus, f = g μ-almost everywhere, as desired.
For σ-finite positive measures
If μ and ν are σ-finite, then X can be written as the union of a sequence {Bn}n of disjoint sets in Σ, each of which has finite measure under both μ and ν. For each n, there is a Σ-measurable function fn : Bn → [0, +∞) such that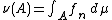
for each Σ-measurable subset A of Bn. The union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
f of those functions is then the required function.
As for the uniqueness, since each of the fn is μ-almost everywhere unique, then so is f.
For signed and complex measures
If ν is a σ-finite signed measure, then it can be Hahn–Jordan decomposed as ν = ν+−ν− where one of the measures is finite. Applying the previous result to those two measures, one obtains two functions, g, h : X → [0, +∞), satisfying the Radon–Nikodym theorem for ν+ and ν− respectively, at least one of which is μ-integrable (i.e., its integral with respect to μ is finite). It is clear then that f = g − h satisfies the required properties, including uniqueness, since both g and h are unique up to μ-almost everywhere equality.If ν is a complex measure
Complex measure
In mathematics, specifically measure theory, a complex measure generalizes the concept of measure by letting it have complex values. In other words, one allows for sets whose size is a complex number.-Definition:...
, it can be decomposed as ν = ν1 + iν2, where both ν1 and ν2 are finite-valued signed measures. Applying the above argument, one obtains two functions, g, h : X → [0, +∞), satisfying the required properties for ν1 and ν2, respectively. Clearly, f = g + i h is the required function.