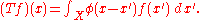Kernel (mathematics)
Encyclopedia
In mathematics
, the word kernel has several meanings. Kernel may mean a subset associated with a mapping
:
Kernel may also mean a function of two variables, which is used to define a mapping:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the word kernel has several meanings. Kernel may mean a subset associated with a mapping
Map (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
:
- The kernel of a mapping is the set of elements that map to the zero elementAdditive identityIn mathematics the additive identity of a set which is equipped with the operation of addition is an element which, when added to any element x in the set, yields x...
(such as zero or zero vectorNull vectorNull vector can refer to:* Null vector * A causal structure in Minkowski space...
), as in kernel of a linear operator and kernel of a matrix. In this context, kernel is often called nullspace. - More generally, the kernel in algebraKernel (algebra)In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
is the set of elements that map to the neutral element. Here, the mapping is assumed to be a homomorphismHomomorphismIn abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
, that is, it preserves algebraic operations, and, in particular, maps neutral element to neutral element. The kernel is then the set of all elements that the mapping cannot distinguish from the neutral element. - The kernel in category theoryKernel (category theory)In category theory and its applications to other branches of mathematics, kernels are a generalization of the kernels of group homomorphisms, the kernels of module homomorphisms and certain other kernels from algebra...
is a generalization of this concept to morphismMorphismIn mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
s rather than mappings between sets. - In set theory, the kernel of a function is the set of all pairs of elements that the function cannot distinguish, that is, they map to the same value. This is a generalization of the kernel concept above to the case when there is no neutral element.
- In set theory, the difference kernel or binary equalizer is the set of all elements where the values of two functions coincide.
Kernel may also mean a function of two variables, which is used to define a mapping:
- In integral calculus, the kernel (also called integral kernel or kernel function) is a function of two variables that defines an integral transform, such as the function k in
- In partial differential equationPartial differential equationIn mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s, when the solution of the equation for the right-hand side f can be written as Tf above, the kernel becomes the Green's functionGreen's functionIn mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
. The heat kernelHeat kernelIn the mathematical study of heat conduction and diffusion, a heat kernel is the fundamental solution to the heat equation on a particular domain with appropriate boundary conditions. It is also one of the main tools in the study of the spectrum of the Laplace operator, and is thus of some...
is the Green's function of the heat equation. - In the case when the integral kernel depends only on the difference between its arguments, it becomes a convolution kernel, as in
- In statisticsStatisticsStatistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, a kernelKernel (statistics)A kernel is a weighting function used in non-parametric estimation techniques. Kernels are used in kernel density estimation to estimate random variables' density functions, or in kernel regression to estimate the conditional expectation of a random variable. Kernels are also used in time-series,...
is a weighting function used in kernel density estimationKernel density estimationIn statistics, kernel density estimation is a non-parametric way of estimating the probability density function of a random variable. Kernel density estimation is a fundamental data smoothing problem where inferences about the population are made, based on a finite data sample...
to estimate the probability density functionProbability density functionIn probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
of a random variableRandom variableIn probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
. - In probability theoryProbability theoryProbability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and statisticsStatisticsStatistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, a stochastic kernelStochastic kernelIn statistics, a stochastic kernel estimate is an estimate of the transition function of a stochastic process. Often, this is an estimate of the conditional density function obtained using kernel density estimation...
is the transition function of a stochastic processStochastic processIn probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
. In a discrete time process with continuous probability distributions, it is the same thing as the kernel of the integral operator that advances the probability density functionProbability density functionIn probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
. - Kernel trickKernel trickFor machine learning algorithms, the kernel trick is a way of mapping observations from a general set S into an inner product space V , without ever having to compute the mapping explicitly, in the hope that the observations will gain meaningful linear structure in V...
is a technique to write a nonlinear operator as a linear one in a space of higher dimension. - In operator theory, a positive definite kernel is a generalization of a positive matrix.
- The kernel in a reproducing kernel Hilbert spaceReproducing kernel Hilbert spaceIn functional analysis , a reproducing kernel Hilbert space is a Hilbert space of functions in which pointwise evaluation is a continuous linear functional. Equivalently, they are spaces that can be defined by reproducing kernels...
.