
Reflexive space
Encyclopedia
In functional analysis
, a Banach space
(or more generally a locally convex topological vector space
) is called reflexive if it coincides with the dual of its dual space
in the topological and algebraic senses. Reflexive Banach spaces are often characterized by their geometric properties.
over R
or C
. We denote by its continuous dual
, i.e. the space of all continuous linear maps from X to the base field. As explained in the dual space article, is a Banach space. We can form the double dual , the continuous dual of . There is a natural continuous linear transformation
defined by
That is, J maps x to the functional on given by evaluation at x. As a consequence of the Hahn–Banach theorem
, J is norm-preserving (i.e., ||J(x)|| = ||x|| ) and hence injective. The space X is called reflexive if J is bijective. (This implies that a reflexive normed space is a Banach space, since X must be isometric to the complete space .) The space X is called quasi-reflexive (of order d) if X ′′/J(X) has finite dimension d.
, the topology of uniform convergence on bounded subsets
of X. Let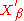 denote this topological vector space, called the strong dual of X. When the canonical embedding J of X into the dual of
denote this topological vector space, called the strong dual of X. When the canonical embedding J of X into the dual of 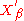 is bijective, then X is said to be semi-reflexive. If, in addition, the topology on X coincides with the strong topology , then X is said to be reflexive.
is bijective, then X is said to be semi-reflexive. If, in addition, the topology on X coincides with the strong topology , then X is said to be reflexive.
Note When applied to normed spaces, the definitions in this section coincide with the notion of reflexivity for normed spaces. Indeed, the norm topology on the dual of a Banach space X coincides with the strong topology , so that, as topological vector space, the normed space is the strong dual of X. Also, the norm topology on X coincides with . Therefore, X is reflexive as topological vector space if and only if it is reflexive as normed space, namely, when the injection J is bijective.
.
The Banach space c0 of scalar sequences tending to 0 at infinity, equipped with the supremum norm, is not reflexive. It follows from the general properties below that ℓ1 and ℓ∞ are not reflexive, because ℓ1 is isomorphic to the dual of c0, and ℓ∞ is isomorphic to the dual of ℓ1.
All Hilbert space
s are reflexive, as are the Lp spaces
for . More generally: all uniformly convex
Banach spaces are reflexive according to the Milman–Pettis theorem
. The L1(μ) and L∞(μ) spaces are not reflexive (unless they are finite dimensional, which happens for example when μ is a measure on a finite set). Likewise, the Banach space C([0, 1]) of continuous functions on [0, 1] is not reflexive.
The spaces Sp(H) of operators in the Schatten class
on a Hilbert space H are uniformly convex, hence reflexive, when . When the dimension of H is infinite, then S1(H) (the trace class
) is not reflexive, because it contains a subspace isomorphic to ℓ1, and S∞(H) = L(H) (the bounded operators) is not reflexive, because it contains a subspace isomorphic to ℓ∞ (in both cases, the subspace can be chosen to be the operators diagonal with respect to a given orthonormal basis of H).
Every finite-dimensional Hausdorff topological vector space
is reflexive, because J is bijective by linear algebra, and because there is a unique Hausdorff vector space topology on a finite dimensional vector space.
Montel space
s are reflexive locally convex topological vector spaces.
Every semi-reflexive normed space is reflexive. A (somewhat artificial) example of a semi-reflexive space, not reflexive, is obtained as follows: let Y be an infinite dimensional reflexive Banach space, and let X be the topological vector space , that is, the vector space Y equipped with the weak topology. Then the continuous dual of X is the set and bounded subsets of X are norm-bounded, hence the Banach space is the strong dual of X. Since Y is reflexive, the continuous dual of is equal to the image J(X) of X under the canonical embedding J, but the topology on X is not the strong topology , that is equal to the norm topology of Y.
Every closed
subspace
of a reflexive space is reflexive. The dual of a reflexive space is reflexive. Every quotient
of a reflexive space is reflexive.
The promised geometric property of reflexive Banach spaces is the following: if C is a closed non-empty convex
subset of the reflexive space X, then for every x in X there exists a c in C such that ||x − c|| minimizes the distance between x and points of C. (Note that while the minimal distance between x and C is uniquely defined by x, the point c is not. The closest point c is unique when X is uniformly convex.)
Let X be a Banach space. The following are equivalent.
A reflexive Banach space is separable if and only if its dual is separable. This follows from the fact that for every normed space Y, separability of the dual implies separability .
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, a Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
(or more generally a locally convex topological vector space
Locally convex topological vector space
In functional analysis and related areas of mathematics, locally convex topological vector spaces or locally convex spaces are examples of topological vector spaces which generalize normed spaces. They can be defined as topological vector spaces whose topology is generated by translations of ...
) is called reflexive if it coincides with the dual of its dual space
Dual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
in the topological and algebraic senses. Reflexive Banach spaces are often characterized by their geometric properties.
Normed spaces
Suppose X is a normed vector spaceNormed vector space
In mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
over R
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
or C
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
. We denote by its continuous dual
Dual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
, i.e. the space of all continuous linear maps from X to the base field. As explained in the dual space article, is a Banach space. We can form the double dual , the continuous dual of . There is a natural continuous linear transformation
- J : X →
defined by
- J(x)(φ) = φ(x) for every x in X and φ .
That is, J maps x to the functional on given by evaluation at x. As a consequence of the Hahn–Banach theorem
Hahn–Banach theorem
In mathematics, the Hahn–Banach theorem is a central tool in functional analysis. It allows the extension of bounded linear functionals defined on a subspace of some vector space to the whole space, and it also shows that there are "enough" continuous linear functionals defined on every normed...
, J is norm-preserving (i.e., ||J(x)|| = ||x|| ) and hence injective. The space X is called reflexive if J is bijective. (This implies that a reflexive normed space is a Banach space, since X must be isometric to the complete space .) The space X is called quasi-reflexive (of order d) if X ′′/J(X) has finite dimension d.
Locally convex spaces
When X is a locally convex topological vector space, the continuous dual can be equipped with the strong topologyStrong topology (polar topology)
In functional analysis and related areas of mathematics the strong topology is the finest polar topology, the topology with the most open sets, on a dual pair...
, the topology of uniform convergence on bounded subsets
Bounded set (topological vector space)
In functional analysis and related areas of mathematics, a set in a topological vector space is called bounded or von Neumann bounded, if every neighborhood of the zero vector can be inflated to include the set...
of X. Let
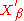 denote this topological vector space, called the strong dual of X. When the canonical embedding J of X into the dual of
denote this topological vector space, called the strong dual of X. When the canonical embedding J of X into the dual of 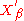 is bijective, then X is said to be semi-reflexive. If, in addition, the topology on X coincides with the strong topology , then X is said to be reflexive.
is bijective, then X is said to be semi-reflexive. If, in addition, the topology on X coincides with the strong topology , then X is said to be reflexive.Note When applied to normed spaces, the definitions in this section coincide with the notion of reflexivity for normed spaces. Indeed, the norm topology on the dual of a Banach space X coincides with the strong topology , so that, as topological vector space, the normed space is the strong dual of X. Also, the norm topology on X coincides with . Therefore, X is reflexive as topological vector space if and only if it is reflexive as normed space, namely, when the injection J is bijective.
Examples
Every finite-dimensional normed space is reflexive, simply because in this case, the space, its dual and bidual all have the same linear dimension, hence the linear injection J from the definition is bijective, by the rank-nullity theoremRank-nullity theorem
In mathematics, the rank–nullity theorem of linear algebra, in its simplest form, states that the rank and the nullity of a matrix add up to the number of columns of the matrix. Specifically, if A is an m-by-n matrix over some field, thenThis applies to linear maps as well...
.
The Banach space c0 of scalar sequences tending to 0 at infinity, equipped with the supremum norm, is not reflexive. It follows from the general properties below that ℓ1 and ℓ∞ are not reflexive, because ℓ1 is isomorphic to the dual of c0, and ℓ∞ is isomorphic to the dual of ℓ1.
All Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s are reflexive, as are the Lp spaces
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
for . More generally: all uniformly convex
Uniformly convex space
In mathematics, uniformly convex spaces are common examples of reflexive Banach spaces. The concept of uniform convexity was first introduced by James A...
Banach spaces are reflexive according to the Milman–Pettis theorem
Milman–Pettis theorem
In mathematics, the Milman–Pettis theorem states that every uniformly convex Banach space is reflexive.The theorem was proved independently by D. Milman and B. J. Pettis . S. Kakutani gave a different proof in , and John R. Ringrose published a shorter proof in 1959.- References :* S. Kakutani,...
. The L1(μ) and L∞(μ) spaces are not reflexive (unless they are finite dimensional, which happens for example when μ is a measure on a finite set). Likewise, the Banach space C([0, 1]) of continuous functions on [0, 1] is not reflexive.
The spaces Sp(H) of operators in the Schatten class
Schatten class operator
In mathematics, specifically functional analysis, a pth Schatten-class operator is a bounded linear operator on a Hilbert space with finite pth Schatten norm. The space of pth Schatten-class operators is a Banach space with respect to the Schatten norm.Via polar decomposition, one can prove that...
on a Hilbert space H are uniformly convex, hence reflexive, when . When the dimension of H is infinite, then S1(H) (the trace class
Trace class
In mathematics, a trace class operator is a compact operator for which a trace may be defined, such that the trace is finite and independent of the choice of basis....
) is not reflexive, because it contains a subspace isomorphic to ℓ1, and S∞(H) = L(H) (the bounded operators) is not reflexive, because it contains a subspace isomorphic to ℓ∞ (in both cases, the subspace can be chosen to be the operators diagonal with respect to a given orthonormal basis of H).
Every finite-dimensional Hausdorff topological vector space
Topological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
is reflexive, because J is bijective by linear algebra, and because there is a unique Hausdorff vector space topology on a finite dimensional vector space.
Montel space
Montel space
In functional analysis and related areas of mathematics a Montel space, named after Paul Montel, is any topological vector space in which an analog of Montel's theorem holds. Specifically, a Montel space is a barrelled topological vector space where every closed and bounded set is compact...
s are reflexive locally convex topological vector spaces.
Every semi-reflexive normed space is reflexive. A (somewhat artificial) example of a semi-reflexive space, not reflexive, is obtained as follows: let Y be an infinite dimensional reflexive Banach space, and let X be the topological vector space , that is, the vector space Y equipped with the weak topology. Then the continuous dual of X is the set and bounded subsets of X are norm-bounded, hence the Banach space is the strong dual of X. Since Y is reflexive, the continuous dual of is equal to the image J(X) of X under the canonical embedding J, but the topology on X is not the strong topology , that is equal to the norm topology of Y.
Properties
If a Banach space Y is isomorphic to a reflexive Banach space X, then Y is reflexive.Every closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
subspace
Linear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
of a reflexive space is reflexive. The dual of a reflexive space is reflexive. Every quotient
Quotient space (linear algebra)
In linear algebra, the quotient of a vector space V by a subspace N is a vector space obtained by "collapsing" N to zero. The space obtained is called a quotient space and is denoted V/N ....
of a reflexive space is reflexive.
The promised geometric property of reflexive Banach spaces is the following: if C is a closed non-empty convex
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
subset of the reflexive space X, then for every x in X there exists a c in C such that ||x − c|| minimizes the distance between x and points of C. (Note that while the minimal distance between x and C is uniquely defined by x, the point c is not. The closest point c is unique when X is uniformly convex.)
Let X be a Banach space. The following are equivalent.
- The space X is reflexive.
- The dual of X is reflexive.
- The closed unit ball of X is compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
in the weak topologyWeak topologyIn mathematics, weak topology is an alternative term for initial topology. The term is most commonly used for the initial topology of a topological vector space with respect to its continuous dual...
. - Every bounded sequence in X has a weakly convergent subsequence.
- Every continuous linear functional on X attains its maximum on the closed unit ball in X. (James' theoremJames' theoremIn mathematics, particularly functional analysis, James' theorem, named for Robert C. James, states that a Banach space B is reflexive if and only if every continuous linear functional on B attains its maximum on the closed unit ball in B....
)
A reflexive Banach space is separable if and only if its dual is separable. This follows from the fact that for every normed space Y, separability of the dual implies separability .
See also
- A generalization which has some of the properties of reflexive space and includes many spaces of practical importance is Grothendieck spaceGrothendieck spaceIn mathematics, a Grothendieck space, named for Alexander Grothendieck, is a Banach space X such that for all separable Banach spaces Y, every bounded linear operator from X to Y is weakly compact, that is, the image of a bounded subset of X is a weakly compact subset of Y.Every reflexive Banach...
- Reflexive operator algebraReflexive operator algebraIn functional analysis, a reflexive operator algebra A is an operator algebra that has enough invariant subspaces to characterize it. Formally, A is reflexive if it is equal to the algebra of bounded operators which leave invariant each subspace left invariant by every operator in A.This should not...

