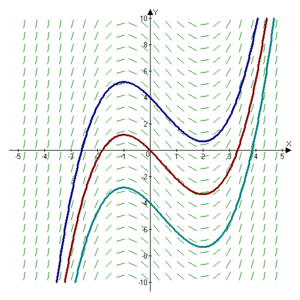
Integral curve
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an integral curve is a parametric curve that represents a specific solution to an ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
or system of equations. If the differential equation is represented as a vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
or slope field
Slope field
In mathematics, a slope field is a graphical representation of the solutions of a first-order differential equation. It is achieved without solving the differential equation analytically, and thus it is useful...
, then the corresponding integral curves are tangent
Tangent
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
to the field at each point.
Integral curves are known by various other names, depending on the nature and interpretation of the differential equation or vector field. In physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, integral curves for an electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
or magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
are known as field line
Field line
A field line is a locus that is defined by a vector field and a starting location within the field. Field lines are useful for visualizing vector fields, which are otherwise hard to depict...
s, and integral curves for the velocity field of a fluid
Fluid
In physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
are known as flow lines. In dynamical systems
Dynamical systems theory
Dynamical systems theory is an area of applied mathematics used to describe the behavior of complex dynamical systems, usually by employing differential equations or difference equations. When differential equations are employed, the theory is called continuous dynamical systems. When difference...
, the integral curves for a differential equation that governs a system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
are referred to as trajectories
Trajectory
A trajectory is the path that a moving object follows through space as a function of time. The object might be a projectile or a satellite, for example. It thus includes the meaning of orbit—the path of a planet, an asteroid or a comet as it travels around a central mass...
or orbits
Orbit (dynamics)
In mathematics, in the study of dynamical systems, an orbit is a collection of points related by the evolution function of the dynamical system. The orbit is a subset of the phase space and the set of all orbits is a partition of the phase space, that is different orbits do not intersect in the...
.
The name “integral curve” derives from an obsolete meaning for the word “integral”. Historically, the operation of solving a differential equation was known as “integrating” the equation, and the solutions were known as “integrals”.
Definition
Suppose that F is a vector fieldVector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
: that is, a vector-valued function
Vector-valued function
A vector-valued function also referred to as a vector function is a mathematical function of one or more variables whose range is a set of multidimensional vectors or infinite-dimensional vectors. The input of a vector-valued function could be a scalar or a vector...
with cartesian coordinates (F1,F2,...,Fn); and x(t) a parametric curve with cartesian coordinates (x1(t),x2(t),...,xn(t)). Then x(t) is an integral curve of F if it is a solution of the following autonomous system
Autonomous system (mathematics)
In mathematics, an autonomous system or autonomous differential equation is a system of ordinary differential equations which does not explicitly depend on the independent variable...
of ordinary differential equations:
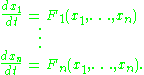
Such a system may be written as a single vector equation

This equation says precisely that the tangent vector to the curve at any point x(t) along the curve is precisely the vector F(x(t)), and so the curve x(t) is tangent at each point to the vector field F.
If a given vector field is Lipschitz continuous, then the Picard–Lindelöf theorem
Picard–Lindelöf theorem
In mathematics, in the study of differential equations, the Picard–Lindelöf theorem, Picard's existence theorem or Cauchy–Lipschitz theorem is an important theorem on existence and uniqueness of solutions to first-order equations with given initial conditions.The theorem is named after Charles...
implies that there exists a unique flow for small time.
Definition
Let M be a Banach manifoldBanach manifold
In mathematics, a Banach manifold is a manifold modeled on Banach spaces. Thus it is a topological space in which each point has a neighbourhood homeomorphic to an open set in a Banach space...
of class Cr with r ≥ 2. As usual, TM denotes the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
of M with its natural projection
Projection (mathematics)
Generally speaking, in mathematics, a projection is a mapping of a set which is idempotent, which means that a projection is equal to its composition with itself. A projection may also refer to a mapping which has a left inverse. Bot notions are strongly related, as follows...
πM : TM → M given by
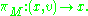
A vector field on M is a cross-section of the tangent bundle TM, i.e. an assignment to every point of the manifold M of a tangent vector to M at that point. Let X be a vector field on M of class Cr−1 and let p ∈ M. An integral curve for X passing through p at time t0 is a curve α : J → M of class Cr−1, defined on an open interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
J of the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
R containing t0, such that
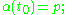
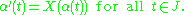
Relationship to ordinary differential equations
The above definition of an integral curve α for a vector field X, passing through p at time t0, is the same as saying that α is a local solution to the ordinary differential equation/initial value problem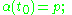
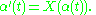
It is local in the sense that it is defined only for times in J, and not necessarily for all t ≥ t0 (let alone t ≤ t0). Thus, the problem of proving the existence and uniqueness of integral curves is the same as that of finding solutions to ordinary differential equations/initial value problems and showing that they are unique.
Remarks on the time derivative
In the above, α′(t) denotes the derivative of α at time t, the "direction α is pointing" at time t. From a more abstract viewpoint, this is the Fréchet derivativeFréchet derivative
In mathematics, the Fréchet derivative is a derivative defined on Banach spaces. Named after Maurice Fréchet, it is commonly used to formalize the concept of the functional derivative used widely in the calculus of variations. Intuitively, it generalizes the idea of linear approximation from...
:
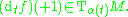
In the special case that M is some open subset of Rn, this is the familiar derivative

where α1, ..., αn are the coordinates for α with respect to the usual coordinate directions.
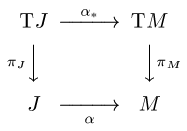
The same thing may be phrased even more abstractly in terms of induced maps. Note that the tangent bundle TJ of J is the trivial bundle J × R and there is a canonical cross-section ι of this bundle such that ι(t) = 1 (or, more precisely, (t, 1)) for all t ∈ J. The curve α induces a bundle map
Bundle map
In mathematics, a bundle map is a morphism in the category of fiber bundles. There are two distinct, but closely related, notions of bundle map, depending on whether the fiber bundles in question have a common base space. There are also several variations on the basic theme, depending on precisely...
α∗ : TJ → TM so that the following diagram commutes:
Then the time derivative α′ is the composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
α′ = α∗ o ι, and α′(t) is its value at some point t ∈ J.