Dynamical systems theory
Encyclopedia
Dynamical systems theory is an area of applied mathematics
used to describe the behavior of complex
dynamical system
s, usually by employing differential equations or difference equations. When differential equations are employed, the theory is called continuous dynamical systems. When difference equations are employed, the theory is called discrete dynamical systems. When the time variable runs over a set which is discrete over some intervals and continuous over other intervals or is any arbitrary time-set such as a cantor set
then one gets dynamic equations on time scales. Some situations may also be modelled by mixed operators such as differential-difference equations.
This theory deals with the long-term qualitative behavior of dynamical systems, and the studies of the solutions to the equations of motion of systems that are primarily mechanical
in nature; although this includes both planetary orbit
s as well as the behaviour of electronic circuit
s and the solutions to partial differential equation
s that arise in biology
. Much of modern research is focused on the study of chaotic systems.
This field of study is also called just Dynamical systems, Systems theory or longer as Mathematical Dynamical Systems Theory and the Mathematical theory of dynamical systems.

deal with the long-term qualitative behavior of dynamical system
s. Here, the focus is not on finding precise solutions to the equations defining the dynamical system (which is often hopeless), but rather to answer questions like "Will the system settle down to a steady state in the long term, and if so, what are the possible steady states?", or "Does the long-term behavior of the system depend on its initial condition?"
An important goal is to describe the fixed points, or steady states of a given dynamical system; these are values of the variable which won't change over time. Some of these fixed points are attractive, meaning that if the system starts out in a nearby state, it will converge towards the fixed point.
Similarly, one is interested in periodic points, states of the system which repeat themselves after several timesteps. Periodic points can also be attractive. Sarkovskii's theorem
is an interesting statement about the number of periodic points of a one-dimensional discrete dynamical system.
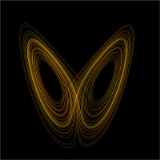
Even simple nonlinear dynamical systems often exhibit almost random, completely unpredictable behavior that has been called chaos. The branch of dynamical systems which deals with the clean definition and investigation of chaos is called chaos theory.
Before the advent of fast computing machines
, solving a dynamical system required sophisticated mathematical techniques and could only be accomplished for a small class of dynamical systems.
Some excellent presentations of mathematical dynamic system theory include Beltrami (1987), Luenberger (1979), Padulo and Arbib (1974), and Strogatz (1994).
concept is a mathematical formalization
for any fixed "rule" which describes the time
dependence of a point's position in its ambient space
. Examples include the mathematical model
s that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each spring in a lake.
A dynamical system has a state determined by a collection of real numbers, or more generally by a set of points
in an appropriate state space. Small changes in the state of the system correspond to small changes in the numbers. The numbers are also the coordinates of a geometrical space—a manifold
. The evolution rule of the dynamical system is a fixed rule
that describes what future states follow from the current state. The rule is deterministic
: for a given time interval only one future state follows from the current state.
, also termed the dynamic hypothesis or the dynamic hypothesis in cognitive science or dynamic cognition, is a new approach in cognitive science
exemplified by the work of philosopher Tim van Gelder
. It argues that differential equations are more suited to modelling cognition
than more traditional computer
models.
, a nonlinear system is a system which is not linear
, i.e. a system which does not satisfy the superposition principle
. Less technically, a nonlinear system is any problem where the variable(s) to be solved for cannot be written as a linear sum of independent components. A nonhomogenous system, which is linear apart from the presence of a function of the independent variable
s, is nonlinear according to a strict definition, but such systems are usually studied alongside linear systems, because they can be transformed to a linear system as long as a particular solution is known.
, dynamical systems theory has emerged in the movement sciences as a viable framework for modeling athletic performance. From a dynamical systems perspective, the human movement system is a highly intricate network of co-dependent sub-systems (e.g. respiratory, circulatory, nervous, skeletomuscular, perceptual) that are composed of a large number of interacting components (e.g. blood cells, oxygen molecules, muscle tissue, metabolic enzymes, connective tissue and bone). In dynamical systems theory, movement patterns emerge through generic processes of self-organization found in physical and biological systems.
, especially in the neo-Piagetian theories of cognitive development. It is the belief that cognitive development is best represented by physical theories rather than theories based on syntax and AI
. It also believes that differential equations are the most appropriate tool for modeling human behavior. These equations are interpreted to represent an agent's cognitive trajectory through state space
. In other words, dynamicists argue that psychology
should be (or is) the description (via differential equations) of the cognitions and behaviors of an agent under certain environmental and internal pressures. The language of chaos theory is also frequently adopted.
In it, the learner's mind reaches a state of disequilibrium where old patterns have broken down. This is the phase transition of cognitive development. Self organization (the spontaneous creation of coherent forms) sets in as activity levels link to each other. Newly formed macroscopic and microscopic structures support each other, speeding up the process. These links form the structure of a new state of order in the mind through a process called scalloping (the repeated building up and collapsing of complex performance.) This new, novel state is progressive, discrete, idiosyncratic and unpredictable.
Dynamic systems theory has recently been used to explain a long-unanswered problem in child development referred to as the A-not-B error
.
According to Miller (2002), dynamic systems theory is the broadest and most encompassing of all the developmental theories. This theory attempts to encompass all the possible factors that may be in operation at any given developmental moment; it considers development from many levels (from molecular to cultural) and time scales (from milliseconds to years). Development is viewed as constant, fluid, emergent or non-linear, and multidetermined . Dynamic systems theory’s greatest impact has been in early sensorimotor development .
Esther Thelen believed that development involved a deeply embedded and continuously coupled dynamic system. The typical view presented by R.D. Beer showed that information from the world was given to the nervous system
which directs the body, which intern interacts back on the world. Esther Thelen instead offers a developmental system that has continual and bidirectional interaction between the world, nervous system and body.
The dynamic systems view of development has three critical features that separate it from the traditional input-output model. The system must first be multiply causal and self-organizing. This means that behavior is a pattern formed from multiple components in cooperation with none being more privileged than another. The relationship between the multiple parts is what helps provide order and pattern to the system. Second, a dynamic system is a dependent on time making the current state a function of the previous state and the future state a function of the current state. The third feature is the relative stability of a dynamic system. For a system to change, a loose stability is needed to allow for the components to reorganize into a different expressed behavior. Development is a sequence of times where stability is low allowing for new development and where stability is stable with less pattern change.
Esther Thelen's early research in infant motor behavior (particularly stepping, kicking, and reaching) led her to become dissatisfied with existing theories and moved her toward a dynamic systems perspective. Prior views of development conceptualized infants as passive and infants’ motor development as the result of a genetically determined developmental plan. Thelen, in her work, discovered that infants' body weights and proportions, postures, elastic, and inertial properties of muscle and the nature of the task and environment contribute equally to the motor outcome. Infants can "self-assemble" new motor patterns in novel situations. Development happens in individual children solving individual problems in their own unique ways . Because each child is different in terms of his or her body, nervous system, and daily experience, the course of development is nearly impossible to predict. There are multiple pathways to development . Development is not just the result of genetics or the environment, but rather the interweaving of events at a given moment . Dynamic systems theory’s greatest impact has been in early sensorimotor development .
Related scientists
Applied mathematics
Applied mathematics is a branch of mathematics that concerns itself with mathematical methods that are typically used in science, engineering, business, and industry. Thus, "applied mathematics" is a mathematical science with specialized knowledge...
used to describe the behavior of complex
Complex systems
Complex systems present problems in mathematical modelling.The equations from which complex system models are developed generally derive from statistical physics, information theory and non-linear dynamics, and represent organized but unpredictable behaviors of systems of nature that are considered...
dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
s, usually by employing differential equations or difference equations. When differential equations are employed, the theory is called continuous dynamical systems. When difference equations are employed, the theory is called discrete dynamical systems. When the time variable runs over a set which is discrete over some intervals and continuous over other intervals or is any arbitrary time-set such as a cantor set
Cantor set
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
then one gets dynamic equations on time scales. Some situations may also be modelled by mixed operators such as differential-difference equations.
This theory deals with the long-term qualitative behavior of dynamical systems, and the studies of the solutions to the equations of motion of systems that are primarily mechanical
Mechanics
Mechanics is the branch of physics concerned with the behavior of physical bodies when subjected to forces or displacements, and the subsequent effects of the bodies on their environment....
in nature; although this includes both planetary orbit
Planetary orbit
In physics, an orbit is the gravitationally curved path of an object around a point in space, for example the orbit of a planet around the center of a star system, such as the Solar System...
s as well as the behaviour of electronic circuit
Electronic circuit
An electronic circuit is composed of individual electronic components, such as resistors, transistors, capacitors, inductors and diodes, connected by conductive wires or traces through which electric current can flow...
s and the solutions to partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s that arise in biology
Biology
Biology is a natural science concerned with the study of life and living organisms, including their structure, function, growth, origin, evolution, distribution, and taxonomy. Biology is a vast subject containing many subdivisions, topics, and disciplines...
. Much of modern research is focused on the study of chaotic systems.
This field of study is also called just Dynamical systems, Systems theory or longer as Mathematical Dynamical Systems Theory and the Mathematical theory of dynamical systems.

Overview
Dynamical systems theory and chaos theoryChaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
deal with the long-term qualitative behavior of dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
s. Here, the focus is not on finding precise solutions to the equations defining the dynamical system (which is often hopeless), but rather to answer questions like "Will the system settle down to a steady state in the long term, and if so, what are the possible steady states?", or "Does the long-term behavior of the system depend on its initial condition?"
An important goal is to describe the fixed points, or steady states of a given dynamical system; these are values of the variable which won't change over time. Some of these fixed points are attractive, meaning that if the system starts out in a nearby state, it will converge towards the fixed point.
Similarly, one is interested in periodic points, states of the system which repeat themselves after several timesteps. Periodic points can also be attractive. Sarkovskii's theorem
Sarkovskii's theorem
In mathematics, Sharkovskii's theorem, named after Oleksandr Mikolaiovich Sharkovsky, is a result about discrete dynamical systems. One of the implications of the theorem is that if a continuous discrete dynamical system on the real line has a periodic point of period 3, then it must have...
is an interesting statement about the number of periodic points of a one-dimensional discrete dynamical system.
Even simple nonlinear dynamical systems often exhibit almost random, completely unpredictable behavior that has been called chaos. The branch of dynamical systems which deals with the clean definition and investigation of chaos is called chaos theory.
History
The concept of dynamical systems theory has its origins in Newtonian mechanics. There, as in other natural sciences and engineering disciplines, the evolution rule of dynamical systems is given implicitly by a relation that gives the state of the system only a short time into the future.Before the advent of fast computing machines
Computer
A computer is a programmable machine designed to sequentially and automatically carry out a sequence of arithmetic or logical operations. The particular sequence of operations can be changed readily, allowing the computer to solve more than one kind of problem...
, solving a dynamical system required sophisticated mathematical techniques and could only be accomplished for a small class of dynamical systems.
Some excellent presentations of mathematical dynamic system theory include Beltrami (1987), Luenberger (1979), Padulo and Arbib (1974), and Strogatz (1994).
Dynamical systems
The dynamical systemDynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
concept is a mathematical formalization
Formal system
In formal logic, a formal system consists of a formal language and a set of inference rules, used to derive an expression from one or more other premises that are antecedently supposed or derived . The axioms and rules may be called a deductive apparatus...
for any fixed "rule" which describes the time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
dependence of a point's position in its ambient space
Ambient space
An ambient space, ambient configuration space, or electroambient space, is the space surrounding an object.-Mathematics:In mathematics, especially in geometry and topology, an ambient space is the space surrounding a mathematical object...
. Examples include the mathematical model
Mathematical model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used not only in the natural sciences and engineering disciplines A mathematical model is a...
s that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each spring in a lake.
A dynamical system has a state determined by a collection of real numbers, or more generally by a set of points
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
in an appropriate state space. Small changes in the state of the system correspond to small changes in the numbers. The numbers are also the coordinates of a geometrical space—a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
. The evolution rule of the dynamical system is a fixed rule
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
that describes what future states follow from the current state. The rule is deterministic
Deterministic system (mathematics)
In mathematics, a deterministic system is a system in which no randomness is involved in the development of future states of the system. A deterministic model will thus always produce the same output from a given starting condition or initial state.-Examples:...
: for a given time interval only one future state follows from the current state.
Dynamicism
DynamicismDynamicism
Dynamicism, also termed the dynamic hypothesis or the dynamic hypothesis in cognitive science or dynamic cognition, is a new approach in cognitive science exemplified by the work of philosopher Tim van Gelder. It argues that differential equations are more suited to modelling cognition than more...
, also termed the dynamic hypothesis or the dynamic hypothesis in cognitive science or dynamic cognition, is a new approach in cognitive science
Cognitive science
Cognitive science is the interdisciplinary scientific study of mind and its processes. It examines what cognition is, what it does and how it works. It includes research on how information is processed , represented, and transformed in behaviour, nervous system or machine...
exemplified by the work of philosopher Tim van Gelder
Tim van Gelder
Tim van Gelder was a founder of Austhink Software, an Australian software development company, and Managing Director of Austhink Consulting. He was born in Australia, educated at the University of Melbourne , the University of Pittsburgh , and held academic positions at Indiana University and the...
. It argues that differential equations are more suited to modelling cognition
Cognition
In science, cognition refers to mental processes. These processes include attention, remembering, producing and understanding language, solving problems, and making decisions. Cognition is studied in various disciplines such as psychology, philosophy, linguistics, and computer science...
than more traditional computer
Computer
A computer is a programmable machine designed to sequentially and automatically carry out a sequence of arithmetic or logical operations. The particular sequence of operations can be changed readily, allowing the computer to solve more than one kind of problem...
models.
Nonlinear system
In mathematicsMathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a nonlinear system is a system which is not linear
Linear system
A linear system is a mathematical model of a system based on the use of a linear operator.Linear systems typically exhibit features and properties that are much simpler than the general, nonlinear case....
, i.e. a system which does not satisfy the superposition principle
Superposition principle
In physics and systems theory, the superposition principle , also known as superposition property, states that, for all linear systems, the net response at a given place and time caused by two or more stimuli is the sum of the responses which would have been caused by each stimulus individually...
. Less technically, a nonlinear system is any problem where the variable(s) to be solved for cannot be written as a linear sum of independent components. A nonhomogenous system, which is linear apart from the presence of a function of the independent variable
Independent variable
The terms "dependent variable" and "independent variable" are used in similar but subtly different ways in mathematics and statistics as part of the standard terminology in those subjects...
s, is nonlinear according to a strict definition, but such systems are usually studied alongside linear systems, because they can be transformed to a linear system as long as a particular solution is known.
Arithmetic dynamics
- Arithmetic dynamicsArithmetic dynamicsArithmetic dynamicsis a field that amalgamates two areas of mathematics, dynamical systems and number theory.Classically, discrete dynamics refers to the study of the iteration of self-maps of the complex plane or real line...
is a field that emerged in the 1990s that amalgamates two areas of mathematics, dynamical systems and number theoryNumber theoryNumber theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
. Classically, discrete dynamics refers to the study of the iterationIterated functionIn mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...
of self-maps of the complex planeComplex planeIn mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
or real lineReal lineIn mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
. Arithmetic dynamics is the study of the number-theoretic properties of integer, rational, -adic, and/or algebraic points under repeated application of a polynomialPolynomialIn mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
or rational functionRational functionIn mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
.
Chaos theory
- Chaos theoryChaos theoryChaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
describes the behavior of certain dynamical systemDynamical system (definition)The dynamical system concept is a mathematical formalization for any fixed "rule" which describes the time dependence of a point's position in its ambient space...
s – that is, systems whose state evolves with time – that may exhibit dynamics that are highly sensitive to initial conditions (popularly referred to as the butterfly effectButterfly effectIn chaos theory, the butterfly effect is the sensitive dependence on initial conditions; where a small change at one place in a nonlinear system can result in large differences to a later state...
). As a result of this sensitivity, which manifests itself as an exponential growth of perturbations in the initial conditions, the behavior of chaotic systems appears to be randomRandomnessRandomness has somewhat differing meanings as used in various fields. It also has common meanings which are connected to the notion of predictability of events....
. This happens even though these systems are deterministicDeterministic system (philosophy)A deterministic system is a conceptual model of the philosophical doctrine of determinism applied to a system for understanding everything that has and will occur in the system, based on the physical outcomes of causality. In a deterministic system, every action, or cause, produces a reaction, or...
, meaning that their future dynamics are fully defined by their initial conditions, with no random elements involved. This behavior is known as deterministic chaos, or simply chaos.
Complex systems
- Complex systemsComplex systemsComplex systems present problems in mathematical modelling.The equations from which complex system models are developed generally derive from statistical physics, information theory and non-linear dynamics, and represent organized but unpredictable behaviors of systems of nature that are considered...
is a scientific field, which studies the common properties of systemSystemSystem is a set of interacting or interdependent components forming an integrated whole....
s considered complexComplexityIn general usage, complexity tends to be used to characterize something with many parts in intricate arrangement. The study of these complex linkages is the main goal of complex systems theory. In science there are at this time a number of approaches to characterizing complexity, many of which are...
in natureNatureNature, in the broadest sense, is equivalent to the natural world, physical world, or material world. "Nature" refers to the phenomena of the physical world, and also to life in general...
, societySocietyA society, or a human society, is a group of people related to each other through persistent relations, or a large social grouping sharing the same geographical or virtual territory, subject to the same political authority and dominant cultural expectations...
and scienceScienceScience is a systematic enterprise that builds and organizes knowledge in the form of testable explanations and predictions about the universe...
. It is also called complex systems theory, complexity science, study of complex systems and/or sciences of complexity. The key problems of such systems are difficulties with their formal modelingScientific modellingScientific modelling is the process of generating abstract, conceptual, graphical and/or mathematical models. Science offers a growing collection of methods, techniques and theory about all kinds of specialized scientific modelling...
and simulationSimulationSimulation is the imitation of some real thing available, state of affairs, or process. The act of simulating something generally entails representing certain key characteristics or behaviours of a selected physical or abstract system....
. From such perspective, in different research contexts complex systems are defined on the base of their different attributes.
- The study of complex systems is bringing new vitality to many areas of science where a more typical reductionist strategy has fallen short. Complex systems is therefore often used as a broad term encompassing a research approach to problems in many diverse disciplines including neurosciences, social sciencesSocial sciencesSocial science is the field of study concerned with society. "Social science" is commonly used as an umbrella term to refer to a plurality of fields outside of the natural sciences usually exclusive of the administrative or managerial sciences...
, meteorologyMeteorologyMeteorology is the interdisciplinary scientific study of the atmosphere. Studies in the field stretch back millennia, though significant progress in meteorology did not occur until the 18th century. The 19th century saw breakthroughs occur after observing networks developed across several countries...
, chemistryChemistryChemistry is the science of matter, especially its chemical reactions, but also its composition, structure and properties. Chemistry is concerned with atoms and their interactions with other atoms, and particularly with the properties of chemical bonds....
, physicsPhysicsPhysics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, computer scienceComputer scienceComputer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, psychologyPsychologyPsychology is the study of the mind and behavior. Its immediate goal is to understand individuals and groups by both establishing general principles and researching specific cases. For many, the ultimate goal of psychology is to benefit society...
, artificial lifeArtificial lifeArtificial life is a field of study and an associated art form which examine systems related to life, its processes, and its evolution through simulations using computer models, robotics, and biochemistry. The discipline was named by Christopher Langton, an American computer scientist, in 1986...
, evolutionary computationEvolutionary computationIn computer science, evolutionary computation is a subfield of artificial intelligence that involves combinatorial optimization problems....
, economicsEconomicsEconomics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
, earthquake prediction, molecular biologyMolecular biologyMolecular biology is the branch of biology that deals with the molecular basis of biological activity. This field overlaps with other areas of biology and chemistry, particularly genetics and biochemistry...
and inquiries into the nature of living cellCell (biology)The cell is the basic structural and functional unit of all known living organisms. It is the smallest unit of life that is classified as a living thing, and is often called the building block of life. The Alberts text discusses how the "cellular building blocks" move to shape developing embryos....
s themselves.
Control theory
- Control theoryControl theoryControl theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
is an interdisciplinary branch of engineeringEngineeringEngineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
and mathematicsMathematicsMathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, that deals with influencing the behavior of dynamical systemDynamical systemA dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
s.
Ergodic theory
- Ergodic theoryErgodic theoryErgodic theory is a branch of mathematics that studies dynamical systems with an invariant measure and related problems. Its initial development was motivated by problems of statistical physics....
is a branch of mathematicsMathematicsMathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
that studies dynamical systemDynamical systemA dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
s with an invariant measureInvariant measureIn mathematics, an invariant measure is a measure that is preserved by some function. Ergodic theory is the study of invariant measures in dynamical systems...
and related problems. Its initial development was motivated by problems of statistical physicsStatistical physicsStatistical physics is the branch of physics that uses methods of probability theory and statistics, and particularly the mathematical tools for dealing with large populations and approximations, in solving physical problems. It can describe a wide variety of fields with an inherently stochastic...
.
Functional analysis
- Functional analysisFunctional analysisFunctional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
is the branch of mathematicsMathematicsMathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, and specifically of analysisMathematical analysisMathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, concerned with the study of vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s and operators acting upon them. It has its historical roots in the study of functional spaces, in particular transformations of functionsFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
, such as the Fourier transformFourier transformIn mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
, as well as in the study of differential and integral equations. This usage of the word functionalFunctional (mathematics)In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
goes back to the calculus of variationsCalculus of variationsCalculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
, implying a function whose argument is a function. Its use in general has been attributed to mathematician and physicist Vito VolterraVito VolterraVito Volterra was an Italian mathematician and physicist, known for his contributions to mathematical biology and integral equations....
and its founding is largely attributed to mathematician Stefan BanachStefan BanachStefan Banach was a Polish mathematician who worked in interwar Poland and in Soviet Ukraine. He is generally considered to have been one of the 20th century's most important and influential mathematicians....
.
Graph dynamical systems
- The concept of graph dynamical systemGraph dynamical systemIn mathematics, the concept of graph dynamical systems can be used to capture a wide range of processes taking place on graphs or networks. A major theme in the mathematical and computational analysis of GDSs is to relate their structural properties and the global dynamics that result.The work on...
s (GDS) can be used to capture a wide range of processes taking place on graphs or networks. A major theme in the mathematical and computational analysis of GDS is to relate their structural properties (e.g. the network connectivity) and the global dynamics that result.
Projected dynamical systems
- Projected dynamical systems is a mathematicalMathematicsMathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
theory investigating the behaviour of dynamical systemDynamical systemA dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
s where solutions are restricted to a constraint set. The discipline shares connections to and applications with both the static world of optimizationOptimization (mathematics)In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
and equilibrium problems and the dynamical world of ordinary differential equations. A projected dynamical system is given by the flowFlow (mathematics)In mathematics, a flow formalizes the idea of the motion of particles in a fluid. Flows are ubiquitous in science, including engineering and physics. The notion of flow is basic to the study of ordinary differential equations. Informally, a flow may be viewed as a continuous motion of points over...
to the projected differential equation.
Symbolic dynamics
- Symbolic dynamicsSymbolic dynamicsIn mathematics, symbolic dynamics is the practice of modeling a topological or smooth dynamical system by a discrete space consisting of infinite sequences of abstract symbols, each of which corresponds to a state of the system, with the dynamics given by the shift operator...
is the practice of modelling a topological or smooth dynamical systemDynamical systemA dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
by a discrete space consisting of infinite sequenceSequenceIn mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
s of abstract symbols, each of which corresponds to a state of the system, with the dynamics (evolution) given by the shift operatorShift operatorIn mathematics, and in particular functional analysis, the shift operator or translation operator is an operator that takes a function to its translation . In time series analysis, the shift operator is called the lag operator....
.
System dynamics
- System dynamicsSystem dynamicsSystem dynamics is an approach to understanding the behaviour of complex systems over time. It deals with internal feedback loops and time delays that affect the behaviour of the entire system. What makes using system dynamics different from other approaches to studying complex systems is the use...
is an approach to understanding the behaviour of complex systemComplex systemA complex system is a system composed of interconnected parts that as a whole exhibit one or more properties not obvious from the properties of the individual parts....
s over time. It deals with internal feedback loops and time delays that affect the behaviour of the entire system. What makes using system dynamics different from other approaches to studying complex systems is the use of feedbackFeedbackFeedback describes the situation when output from an event or phenomenon in the past will influence an occurrence or occurrences of the same Feedback describes the situation when output from (or information about the result of) an event or phenomenon in the past will influence an occurrence or...
loops and stocks and flowsStock and flowEconomics, business, accounting, and related fields often distinguish between quantities that are stocks and those that are flows. These differ in their units of measurement. A stock variable is measured at one specific time, and represents a quantity existing at that point in time , which may have...
. These elements help describe how even seemingly simple systems display baffling nonlinearityNonlinearityIn mathematics, a nonlinear system is one that does not satisfy the superposition principle, or one whose output is not directly proportional to its input; a linear system fulfills these conditions. In other words, a nonlinear system is any problem where the variable to be solved for cannot be...
.
Topological dynamics
- Topological dynamicsTopological dynamicsIn mathematics, topological dynamics is a branch of the theory of dynamical systems in which qualitative, asymptotic properties of dynamical systems are studied from the viewpoint of general topology.- Scope :...
is a branch of the theory of dynamical systems in which qualitative, asymptotic properties of dynamical systems are studied from the viewpoint of general topologyGeneral topologyIn mathematics, general topology or point-set topology is the branch of topology which studies properties of topological spaces and structures defined on them...
.
In biomechanics
In sports biomechanicsSports biomechanics
Sports biomechanics is a quantitative based study and analysis of professional athletes and sports' activities in general. It can simply be described as the Physics of Sports...
, dynamical systems theory has emerged in the movement sciences as a viable framework for modeling athletic performance. From a dynamical systems perspective, the human movement system is a highly intricate network of co-dependent sub-systems (e.g. respiratory, circulatory, nervous, skeletomuscular, perceptual) that are composed of a large number of interacting components (e.g. blood cells, oxygen molecules, muscle tissue, metabolic enzymes, connective tissue and bone). In dynamical systems theory, movement patterns emerge through generic processes of self-organization found in physical and biological systems.
In cognitive science
Dynamical system theory has been applied in the field of neuroscience and cognitive developmentCognitive science
Cognitive science is the interdisciplinary scientific study of mind and its processes. It examines what cognition is, what it does and how it works. It includes research on how information is processed , represented, and transformed in behaviour, nervous system or machine...
, especially in the neo-Piagetian theories of cognitive development. It is the belief that cognitive development is best represented by physical theories rather than theories based on syntax and AI
Ai
AI, A.I., Ai, or ai may refer to:- Computers :* Artificial intelligence, a branch of computer science* Ad impression, in online advertising* .ai, the ISO Internet 2-letter country code for Anguilla...
. It also believes that differential equations are the most appropriate tool for modeling human behavior. These equations are interpreted to represent an agent's cognitive trajectory through state space
State space
In the theory of discrete dynamical systems, a state space is a directed graph where each possible state of a dynamical system is represented by a vertex, and there is a directed edge from a to b if and only if ƒ = b where the function f defines the dynamical system.State spaces are...
. In other words, dynamicists argue that psychology
Psychology
Psychology is the study of the mind and behavior. Its immediate goal is to understand individuals and groups by both establishing general principles and researching specific cases. For many, the ultimate goal of psychology is to benefit society...
should be (or is) the description (via differential equations) of the cognitions and behaviors of an agent under certain environmental and internal pressures. The language of chaos theory is also frequently adopted.
In it, the learner's mind reaches a state of disequilibrium where old patterns have broken down. This is the phase transition of cognitive development. Self organization (the spontaneous creation of coherent forms) sets in as activity levels link to each other. Newly formed macroscopic and microscopic structures support each other, speeding up the process. These links form the structure of a new state of order in the mind through a process called scalloping (the repeated building up and collapsing of complex performance.) This new, novel state is progressive, discrete, idiosyncratic and unpredictable.
Dynamic systems theory has recently been used to explain a long-unanswered problem in child development referred to as the A-not-B error
A-not-B error
A-not-B error is a phenomenon uncovered by the work of Jean Piaget in his theory of cognitive development of children. The A-not-B error is a particular error made by infants during substage 4 of their sensorimotor stage.A typical task goes like this: An experimenter hides an attractive toy under...
.
In Human Development
Dynamic systems theory, as it applies to developmental psychology, was developed by Esther Thelen, Ph.D. at Indiana University-Bloomington. Thelen became interested in developmental psychology through her interest and training in behavioral biology. She wondered if "fixed action patterns," or highly repeatable movements seen in birds and other animals, were also relevant to the control and development of human infantsAccording to Miller (2002), dynamic systems theory is the broadest and most encompassing of all the developmental theories. This theory attempts to encompass all the possible factors that may be in operation at any given developmental moment; it considers development from many levels (from molecular to cultural) and time scales (from milliseconds to years). Development is viewed as constant, fluid, emergent or non-linear, and multidetermined . Dynamic systems theory’s greatest impact has been in early sensorimotor development .
Esther Thelen believed that development involved a deeply embedded and continuously coupled dynamic system. The typical view presented by R.D. Beer showed that information from the world was given to the nervous system
Nervous system
The nervous system is an organ system containing a network of specialized cells called neurons that coordinate the actions of an animal and transmit signals between different parts of its body. In most animals the nervous system consists of two parts, central and peripheral. The central nervous...
which directs the body, which intern interacts back on the world. Esther Thelen instead offers a developmental system that has continual and bidirectional interaction between the world, nervous system and body.
The dynamic systems view of development has three critical features that separate it from the traditional input-output model. The system must first be multiply causal and self-organizing. This means that behavior is a pattern formed from multiple components in cooperation with none being more privileged than another. The relationship between the multiple parts is what helps provide order and pattern to the system. Second, a dynamic system is a dependent on time making the current state a function of the previous state and the future state a function of the current state. The third feature is the relative stability of a dynamic system. For a system to change, a loose stability is needed to allow for the components to reorganize into a different expressed behavior. Development is a sequence of times where stability is low allowing for new development and where stability is stable with less pattern change.
Esther Thelen's early research in infant motor behavior (particularly stepping, kicking, and reaching) led her to become dissatisfied with existing theories and moved her toward a dynamic systems perspective. Prior views of development conceptualized infants as passive and infants’ motor development as the result of a genetically determined developmental plan. Thelen, in her work, discovered that infants' body weights and proportions, postures, elastic, and inertial properties of muscle and the nature of the task and environment contribute equally to the motor outcome. Infants can "self-assemble" new motor patterns in novel situations. Development happens in individual children solving individual problems in their own unique ways . Because each child is different in terms of his or her body, nervous system, and daily experience, the course of development is nearly impossible to predict. There are multiple pathways to development . Development is not just the result of genetics or the environment, but rather the interweaving of events at a given moment . Dynamic systems theory’s greatest impact has been in early sensorimotor development .
See also
Related subjects- List of dynamical system topics
- Baker's mapBaker's mapIn dynamical systems theory, the baker's map is a chaotic map from the unit square into itself. It is named after a kneading operation that bakers apply to dough: the dough is cut in half, and the two halves are stacked on one-another, and compressed...
- Dynamical system (definition)Dynamical system (definition)The dynamical system concept is a mathematical formalization for any fixed "rule" which describes the time dependence of a point's position in its ambient space...
- Embodied Embedded CognitionEmbodied Embedded CognitionEmbodied Embedded Cognition is a philosophical theoretical position in cognitive science, closely related to situated cognition, embodied cognition, embodied cognitive science and dynamical systems theory. The theory states that intelligent behaviour emerges out of the interplay between brain,...
- Gingerbreadman map
- Halo orbitHalo orbitA halo orbit is a periodic, three-dimensional orbit near the , , or Lagrange points in the three-body problem of orbital mechanics. A spacecraft in a halo orbit does not technically orbit the Lagrange point itself , but travels in a closed, repeating path near the Lagrange point...
- List of types of systems theory
- OscillationOscillationOscillation is the repetitive variation, typically in time, of some measure about a central value or between two or more different states. Familiar examples include a swinging pendulum and AC power. The term vibration is sometimes used more narrowly to mean a mechanical oscillation but sometimes...
- PostcognitivismPostcognitivismPsychological movements are considered to be post-cognitivist if they are opposed to or move beyond the cognitivist theories posited by Noam Chomsky, Jerry Fodor, David Marr, and others.Examples of postcognivist propositions:* autopoesis* activity theory...
- Recurrent neural networkRecurrent neural networkA recurrent neural network is a class of neural network where connections between units form a directed cycle. This creates an internal state of the network which allows it to exhibit dynamic temporal behavior. Unlike feedforward neural networks, RNNs can use their internal memory to process...
- Combinatorics and dynamical systemsCombinatorics and dynamical systemsThe mathematical disciplines of combinatorics and dynamical systems interact in a number of ways. The ergodic theory of dynamical systems has recently been used to prove combinatorial theorems about number theory which has given rise to the field of arithmetic combinatorics. Also dynamical systems...
- Synergetics
- SystemographySystemographySystemography or SGR is a process where phenomena regarded as complex are purposefully represented as a constructed model of a general system. It maybe used in three different roles: conceptualization, analysis, and simulation...
Related scientists
- People in systems and controlPeople in systems and controlThis is an alphabetical list of people who have made significant contributions in the fields of system analysis and control theory.-Active researchers:-Historical figures in systems and control:...
- Dmitri Anosov
- Vladimir ArnoldVladimir ArnoldVladimir Igorevich Arnold was a Soviet and Russian mathematician. While he is best known for the Kolmogorov–Arnold–Moser theorem regarding the stability of integrable Hamiltonian systems, he made important contributions in several areas including dynamical systems theory, catastrophe theory,...
- Nikolay BogolyubovNikolay BogolyubovNikolay Nikolaevich Bogolyubov was a Russian and Ukrainian Soviet mathematician and theoretical physicist known for a significant contribution to quantum field theory, classical and quantum statistical mechanics, and to the theory of dynamical systems; a recipient of the Dirac Prize...
- Andrey KolmogorovAndrey KolmogorovAndrey Nikolaevich Kolmogorov was a Soviet mathematician, preeminent in the 20th century, who advanced various scientific fields, among them probability theory, topology, intuitionistic logic, turbulence, classical mechanics and computational complexity.-Early life:Kolmogorov was born at Tambov...
- Nikolay KrylovNikolay Mitrofanovich KrylovNikolay Mitrofanovich Krylov was a Russian and Soviet mathematician known for works on interpolation, non-linear mechanics, and numerical methods for solving equations of mathematical physics.-Biography:...
- Jürgen MoserJürgen MoserJürgen Kurt Moser or Juergen Kurt Moser was a German-American mathematician.-Professional biography:...
- Yakov G. SinaiYakov G. SinaiYakov Grigorevich Sinai is an influential mathematician working in the theory of dynamical systems, in mathematical physics and in probability theory. His work has shaped the modern metric theory of dynamical systems...
- Stephen SmaleStephen SmaleSteven Smale a.k.a. Steve Smale, Stephen Smale is an American mathematician from Flint, Michigan. He was awarded the Fields Medal in 1966, and spent more than three decades on the mathematics faculty of the University of California, Berkeley .-Education and career:He entered the University of...
- Hillel Furstenberg
- Grigory MargulisGrigory MargulisGregori Aleksandrovich Margulis is a Russian mathematician known for his far-reaching work on lattices in Lie groups, and the introduction of methods from ergodic theory into diophantine approximation. He was awarded a Fields Medal in 1978 and a Wolf Prize in Mathematics in 2005, becoming the...
- Elon LindenstraussElon LindenstraussElon Lindenstrauss is an Israeli mathematician, and a winner of the 2010 Fields Medal.Since 2004, he has been a professor at Princeton University...
Further reading
- Frederick David Abraham (1990), A Visual Introduction to Dynamical Systems Theory for Psychology, 1990.
- Beltrami, E. J. (1987). Mathematics for dynamic modeling. NY: Academic Press
- Otomar HájekOtomar HájekOtomar Hájek is a Czech-American mathematician, known for his contributions to dynamical systems, game theory and control theory.He got his Ph.D. at Charles University in Prague on a thesis entitled Dynamical systems in the plane...
(1968}, Dynamical Systems in the Plane. - Luenberger, D. G.David LuenbergerDavid G. Luenberger is a mathematical scientist known for his research and his textbooks, which center on mathematical optimization. He is a professor in the department of Management Science and Engineering at Stanford University.-Biography:...
(1979). Introduction to dynamic systems. NY: Wiley. - Anthony N. Michel, Kaining Wang & Bo Hu (2001), Qualitative Theory of Dynamical Systems: The Role of Stability Preserving Mappings.
- Padulo, L. & Arbib, M A. (1974). System Theory. Philadelphia: Saunders
- Strogatz, S. H.Steven StrogatzSteven Henry Strogatz is an American mathematician and the Jacob Gould Schurman Professor of Applied Mathematics at Cornell University...
(1994), Nonlinear dynamics and chaos. Reading, MA: Addison Wesley
External links
- Dynamic Systems Encyclopedia of Cognitive Science entry.
- Definition of dynamical system in MathWorld.
- DSWeb Dynamical Systems Magazine

