
Hamiltonian optics
Encyclopedia
Lagrangian optics and Hamiltonian optics are two formulations of geometrical optics which share much of the mathematical formalism with Lagrangian mechanics
and Hamiltonian mechanics
.
, Hamilton's principle states that the evolution of a system described by
described by  generalized coordinates
generalized coordinates
between two specified states at two specified parameters σA and σB is a stationary point
(a point where the variation
is zero), of the action
functional
, or
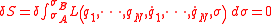
where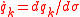 . Condition
. Condition  is valid if and only if the Euler-Lagrange equations are satisfied
is valid if and only if the Euler-Lagrange equations are satisfied
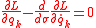
with .
.
The momentum is defined as
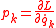
and the Euler-Lagrange equations can then be rewritten as
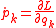
where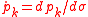 .
.
A different approach to solving this problem consists in defining a Hamiltonian (taking a Legendre transform
of the Lagrangian
) as
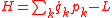
for which a new set of differential equations can be derived by looking at how the total differential of the Lagrangian
depends on parameter σ, positions and their derivatives
and their derivatives 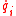 relative to σ. This derivation is the same as in Hamiltonian mechanics, only with time t now replaced by a general parameter σ. Those differential equations are the Hamilton's equations
relative to σ. This derivation is the same as in Hamiltonian mechanics, only with time t now replaced by a general parameter σ. Those differential equations are the Hamilton's equations
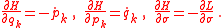
with . Hamilton's equations are first-order differential equation
. Hamilton's equations are first-order differential equation
s, while Euler-Lagrange's equations are second-order.
euclidean space
the generalized coordinates
are now the coordinates of euclidean space
.
. In general, as light travels, it moves in a medium of variable refractive index
which is a scalar field
of position in space, that is,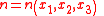 in 3D
in 3D
euclidean space
. Assuming now that light travels along the x3 axis, the path of a light ray may be parametrized as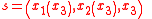 starting at a point
starting at a point 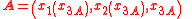 and ending at a point
and ending at a point 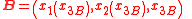 . In this case, when compared to Hamilton's principle above, coordinates
. In this case, when compared to Hamilton's principle above, coordinates 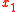 and
and 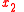 take the role of the generalized coordinates
take the role of the generalized coordinates 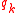 while
while 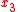 takes the role of parameter
takes the role of parameter  , that is, parameter σ =x3 and N=2.
, that is, parameter σ =x3 and N=2.
In the context of calculus of variations
this can be written as
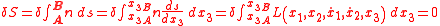
where ds is an infinitesimal displacement along the ray given by and
and
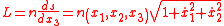
is the optical Lagrangian and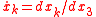 .
.
The optical path length
(OPL) is defined as
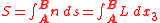
where n is the local refractive index as a function of position along the path between points A and B.
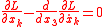
with k=1,2 and where L is the optical Lagrangian and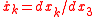 .
.
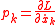
and from the definition of the optical Lagrangian this expression can be rewritten as
this expression can be rewritten as

or in vector form
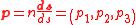
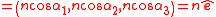
where is a unit vector and angles α1, α2 and α3 are the angles p maxes to axis x1, x2 and x3 respectively, as shown in figure "optical momentum". Therefore the optical momentum is a vector of norm
is a unit vector and angles α1, α2 and α3 are the angles p maxes to axis x1, x2 and x3 respectively, as shown in figure "optical momentum". Therefore the optical momentum is a vector of norm

where n is the refractive index at which p is calculated. Vector p points in the direction of propagation of light. If light is propagating in a gradient index optic
the path of the light ray is curved and vector p is tangent to the light ray.
The expression for the optical path length can also be written as a function of the optical momentum. Having in consideration that the expression for the optical Lagrangian can be rewritten as
the expression for the optical Lagrangian can be rewritten as

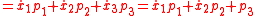
and the expression for the optical path length is

, also in optics the Hamiltonian is defined by the expression given above for N=2 corresponding to functions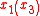 and
and  to be determined
to be determined

Comparing this expression with for the Lagrangian results in
for the Lagrangian results in

And the corresponding Hamilton's equations with parameter σ =x3 and k=1,2 applied to optics are
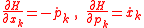
with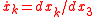 and
and 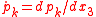 .
.
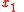 and
and 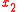 take the role of the generalized coordinates
take the role of the generalized coordinates  while
while 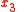 takes the role of parameter
takes the role of parameter  , that is, parameter σ =x3 and N=2.
, that is, parameter σ =x3 and N=2.

and from Hamilton's equations
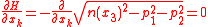
and therefore or
or  for k=1,2.
for k=1,2.
An incoming light ray has momentum pA before refraction (below plane x1x2) and momentum pB after refraction (above plane x1x2). The light ray makes an angle θA with axis x3 (the normal to the refractive surface) before refraction and an angle θB with axis x3 after refraction. Since the p1 and p2 components of the momentum are constant, only p3 changes from p3A to p3B.
Figure "refraction" shows the geometry of this refraction from which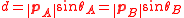 . Since
. Since  and
and  , this last expression can be written as
, this last expression can be written as

which is Snell's law
of refraction
.
In figure "refraction", the normal to the refractive surface points in the direction of axis x3, and also of vector . A unit normal
. A unit normal 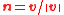 to the refractive surface can then be obtained from the momenta of the incoming and outgoing rays by
to the refractive surface can then be obtained from the momenta of the incoming and outgoing rays by
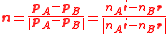
where i and r are a unit vectors in the directions of the incident and refracted rays. Also, the outgoing ray (in the direction of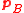 ) is contained in the plane defined by the incoming ray (in the direction of
) is contained in the plane defined by the incoming ray (in the direction of 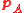 ) and the normal
) and the normal  to the surface.
to the surface.
A similar argument can be used for reflection
in deriving the law of specular reflection
, only now with nA=nB, resulting in θA=θB. Also, if i and r are unit vectors in the directions of the incident and refracted ray respectively, the corresponding normal to the surface is given by the same expression as for refraction, only with nA=nB

In vector form, if i is a unit vector pointing in the direction of the incident ray and n is the unit normal to the surface, the direction r of the refracted ray is given by:
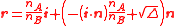
with
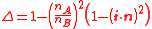
If i·n<0 then -n should be used in the calculations. When , light suffers total internal reflection
, light suffers total internal reflection
and the expression for the reflected ray is that of reflection:
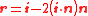
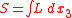
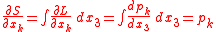
with k=1,2 where the Euler-Lagrange equations with k=1,2 were used. Also, from the last of Hamilton's equations
with k=1,2 were used. Also, from the last of Hamilton's equations 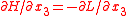 and from
and from  above
above
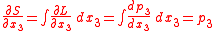
combining the equations for the components of momentum p results in
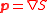
Since p is a vector tangent to the light rays, surfaces S=Constant must be perpendicular to those light rays. These surfaces are called wavefront
s. Figure "rays and wavefronts" illustrates this relationship. Also shown is optical momentum p, tangent to a light ray and perpendicular to the wavefront.
Vector field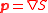 is conservative vector field. The gradient theorem
is conservative vector field. The gradient theorem
can then be applied to the optical path length (as given above) resulting in

and the optical path length S calculated along a curve C between points A and B is a function of only its end points A and B and not the shape of the curve between them. In particular, if the curve is closed, it starts and ends at the same point, or A=B so that
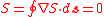
This result may be applied to a closed path ABCDA as in figure "optical path length"
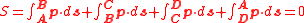
for curve segment AB the optical momentum p is perpendicular to a displacement ds along curve AB, or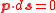 . The same is true for segment CD. For segment BC the optical momentum p has the same direction as displacement ds and
. The same is true for segment CD. For segment BC the optical momentum p has the same direction as displacement ds and 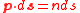 . For segment DA the optical momentum p has the opposite direction to displacement ds and
. For segment DA the optical momentum p has the opposite direction to displacement ds and  . However inverting the direction of the integration so that the integral is taken from A to D, ds inverts direction and
. However inverting the direction of the integration so that the integral is taken from A to D, ds inverts direction and 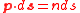 . From these considerations
. From these considerations
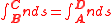
or

and the optical path length SBC between points B and C along the ray connecting them is the same as the optical path length SAD between points A and D along the ray connecting them. The optical path length is constant between wavefronts.
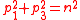 and the direction of a light ray is completely specified by the p1 component of momentum
and the direction of a light ray is completely specified by the p1 component of momentum 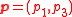 since p2=0. If p1 is given, p3 may be calculated (given the value of the refractive index n) and therefore p1 suffices to determine the direction of the light ray. The refractive index of the medium the ray is traveling in is determined by
since p2=0. If p1 is given, p3 may be calculated (given the value of the refractive index n) and therefore p1 suffices to determine the direction of the light ray. The refractive index of the medium the ray is traveling in is determined by  .
.
For example, ray rC crosses axis x1 at coordinate xB with an optical momentum pC, which has its tip on a circle of radius n centered at position xB. Coordinate xB and the horizontal coordinate p1C of momentum pC completely define ray rC as it crosses axis x1. This ray may then be defined by a point rC=(xB,p1C) in space x1p1 as shown at the bottom of the figure. Space x1p1 is called phase space
and different light rays may be represented by different points in this space.
As such, ray rD shown at the top is represented by a point rD in phase space at the bottom. All rays crossing axis x1 at coordinate xB contained between rays rC and rD are represented by a vertical line connecting points rC and rD in phase space. Accordingly, all rays crossing axis x1 at coordinate xA contained between rays rA and rB are represented by a vertical line connecting points rA and rB in phase space. In general, all rays crossing axis x1 between xL and xR are represented by a volume R in phase space. The rays at the boundary ∂R of volume R are called edge rays. For example, at position xA of axis x1, rays rA and rB are the edge rays since all other rays are contained between these two.
In three-dimensional geometry the optical momentum is given by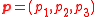 with
with  . If p1 and p2 are given, p3 may be calculated (given the value of the refractive index n) and therefore p1 and p2 suffice to determine the direction of the light ray. A ray traveling along axis x3 is then defined by a point (x1,x2) in plane x1x2 and a direction (p1,p2). It may then be defined by a point in four-dimensional phase space
. If p1 and p2 are given, p3 may be calculated (given the value of the refractive index n) and therefore p1 and p2 suffice to determine the direction of the light ray. A ray traveling along axis x3 is then defined by a point (x1,x2) in plane x1x2 and a direction (p1,p2). It may then be defined by a point in four-dimensional phase space
x1x2p1p2.
This leads to a volume variation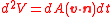 . Making use of Gauss's theorem, the variation in time of the total volume V volume moving in space is
. Making use of Gauss's theorem, the variation in time of the total volume V volume moving in space is

The rightmost term is a volume integral
over the volume V and the middle term is the surface integral
over the boundary A of the volume V. Also, v is the velocity with which the points in V are moving.
In optics coordinate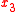 takes the role of time. In phase space a light ray is identified by a point
takes the role of time. In phase space a light ray is identified by a point 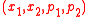 which moves with a "velocity
which moves with a "velocity
" where the dot represents a derivative relative to
where the dot represents a derivative relative to 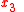 . A set of light rays spreading over
. A set of light rays spreading over 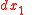 in coordinate
in coordinate 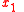 ,
, 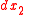 in coordinate
in coordinate 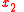 ,
, 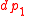 in coordinate
in coordinate 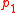 and
and 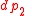 in coordinate
in coordinate  occupies a volume
occupies a volume  in phase space. In general, a large set of rays occupies a large volume
in phase space. In general, a large set of rays occupies a large volume  in phase space to which Gauss's theorem may be applied
in phase space to which Gauss's theorem may be applied
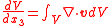
and using Hamilton's equations
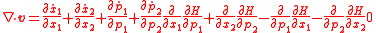
or and
and  which means that the phase space volume is conserved as light travels along an optical system.
which means that the phase space volume is conserved as light travels along an optical system.
The volume occupied by a set of rays in phase space is called etendue
, which is conserved as light rays progress in the optical system along direction x3. This corresponds to Liouville's theorem
, which also applies to Hamiltonian mechanics
.
Light rays crossing the input aperture of the optic at point x1=xI are contained between edge rays rA and rB represented by a vertical line between points rA and rB at the phase space of the input aperture (right, bottom corner of the figure). All rays crossing the input aperture are represented in phase space by a region RI.
Also, light rays crossing the output aperture of the optic at point x1=xO are contained between edge rays rA and rB represented by a vertical line between points rA and rB at the phase space of the output aperture (right, top corner of the figure). All rays crossing the output aperture are represented in phase space by a region RO.
Conservation of etendue in the optical system means that the volume (or area in this two-dimensional case) in phase space occupied by RI at the input aperture must be the same as the volume in phase space occupied by RO at the output aperture.
In imaging optics, all light rays crossing the input aperture at x1=xI are redirected by it towards the output aperture at x1=xO where xI=m xO. This ensures that an image of the input of formed at the output with a magnification m. In phase space, this means that vertical lines in the phase space at the input are transformed into vertical lines at the output. That would be the case of vertical line rA rB in RI transformed to vertical line rA rB in RO.
In nonimaging optics
, the goal is not to form an image but simply to transfer all light from the input aperture to the output aperture. This is accomplished by transforming the edge rays ∂RI of RI to edge rays ∂RO of RO. This is known as the edge ray principle.
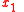 and
and 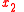 take the role of the generalized coordinates
take the role of the generalized coordinates 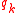 while
while 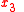 takes the role of parameter
takes the role of parameter  , that is, parameter σ =x3 and N=2. However, different parametrizations of the light rays are possible, as well as the use of generalized coordinates
, that is, parameter σ =x3 and N=2. However, different parametrizations of the light rays are possible, as well as the use of generalized coordinates
.
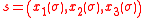 in which σ is a general parameter. In this case, when compared to Hamilton's principle above, coordinates
in which σ is a general parameter. In this case, when compared to Hamilton's principle above, coordinates  ,
, 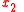 and
and 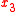 take the role of the generalized coordinates
take the role of the generalized coordinates 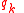 with N=3. Applying Hamilton's principle to optics in this case leads to
with N=3. Applying Hamilton's principle to optics in this case leads to

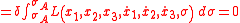
where now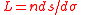 and
and 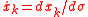 and for which the Euler-Lagrange equations applied to this form of Fermat's principle result in
and for which the Euler-Lagrange equations applied to this form of Fermat's principle result in
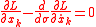
with k=1,2,3 and where L is the optical Lagrangian. Also in this case the optical momentum is defined as

and the Hamiltonian P is defined by the expression given above for N=3 corresponding to functions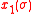 ,
, 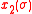 and
and 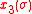 to be determined
to be determined
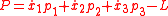
And the corresponding Hamilton's equations with k=1,2,3 applied optics are

with and
and 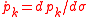 .
.
The optical Lagrangian is given by

and does not explicitly depend on parameter σ. For that reason not all solutions of the Euler-Lagrange equations will be possible light rays, since their derivation assumed an explicit dependence of L on σ which does not happen in optics.
The optical momentum components can be obtained from

where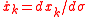 . The expression for the Lagrangian can be rewritten as
. The expression for the Lagrangian can be rewritten as
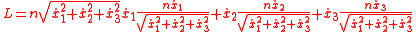

Comparing this expression for L with that for the Hamiltonian P it can be concluded that

From the expressions for the components of the optical momentum results
of the optical momentum results
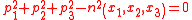
The optical Hamiltonian is chosen as

although other choices could be made. The Hamilton's equations with k=1,2,3 defined above together with define the possible light rays.
define the possible light rays.
, it is also possible to write the equations of Hamiltonian optics in terms of generalized coordinates
 , generalized momenta
, generalized momenta 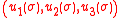 and Hamiltonian P as
and Hamiltonian P as
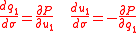
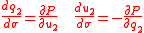
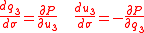
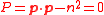
where the optical momentum is given by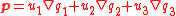


and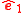 ,
,  and
and  are unit vectors. A particular case is obtained when these vectors form a orthonormal basis
are unit vectors. A particular case is obtained when these vectors form a orthonormal basis
, that is, they are all perpendicular to each other. In that case,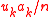 is the cosine of the angle the optical momentum
is the cosine of the angle the optical momentum 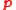 makes to unit vector
makes to unit vector  .
.
Lagrangian mechanics
Lagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
and Hamiltonian mechanics
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
.
Hamilton's principle
In physicsPhysics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, Hamilton's principle states that the evolution of a system
 described by
described by  generalized coordinates
generalized coordinatesGeneralized coordinates
In the study of multibody systems, generalized coordinates are a set of coordinates used to describe the configuration of a system relative to some reference configuration....
between two specified states at two specified parameters σA and σB is a stationary point
Stationary point
In mathematics, particularly in calculus, a stationary point is an input to a function where the derivative is zero : where the function "stops" increasing or decreasing ....
(a point where the variation
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
is zero), of the action
Action (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
functional
Functional (mathematics)
In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
, or
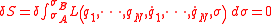
where
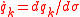 . Condition
. Condition  is valid if and only if the Euler-Lagrange equations are satisfied
is valid if and only if the Euler-Lagrange equations are satisfied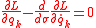
with
 .
.The momentum is defined as
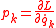
and the Euler-Lagrange equations can then be rewritten as
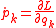
where
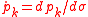 .
.A different approach to solving this problem consists in defining a Hamiltonian (taking a Legendre transform
Legendre transformation
In mathematics, the Legendre transformation or Legendre transform, named after Adrien-Marie Legendre, is an operation that transforms one real-valued function of a real variable into another...
of the Lagrangian
Lagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
) as
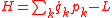
for which a new set of differential equations can be derived by looking at how the total differential of the Lagrangian
Lagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
depends on parameter σ, positions
 and their derivatives
and their derivatives 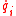 relative to σ. This derivation is the same as in Hamiltonian mechanics, only with time t now replaced by a general parameter σ. Those differential equations are the Hamilton's equations
relative to σ. This derivation is the same as in Hamiltonian mechanics, only with time t now replaced by a general parameter σ. Those differential equations are the Hamilton's equations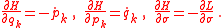
with
 . Hamilton's equations are first-order differential equation
. Hamilton's equations are first-order differential equationDifferential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s, while Euler-Lagrange's equations are second-order.
Lagrangian and Hamiltonian optics
The general results presented above for Hamilton's principle can be applied to optics. In 3DThree-dimensional space
Three-dimensional space is a geometric 3-parameters model of the physical universe in which we live. These three dimensions are commonly called length, width, and depth , although any three directions can be chosen, provided that they do not lie in the same plane.In physics and mathematics, a...
euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
the generalized coordinates
Generalized coordinates
In the study of multibody systems, generalized coordinates are a set of coordinates used to describe the configuration of a system relative to some reference configuration....
are now the coordinates of euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
.
Fermat's principle
Fermat's principle states that the optical length of the path followed by light between two fixed points, A and B, is an extremum. It may be a maximum, a minimum, constant or an inflection pointInflection point
In differential calculus, an inflection point, point of inflection, or inflection is a point on a curve at which the curvature or concavity changes sign. The curve changes from being concave upwards to concave downwards , or vice versa...
. In general, as light travels, it moves in a medium of variable refractive index
Refractive index
In optics the refractive index or index of refraction of a substance or medium is a measure of the speed of light in that medium. It is expressed as a ratio of the speed of light in vacuum relative to that in the considered medium....
which is a scalar field
Scalar field
In mathematics and physics, a scalar field associates a scalar value to every point in a space. The scalar may either be a mathematical number, or a physical quantity. Scalar fields are required to be coordinate-independent, meaning that any two observers using the same units will agree on the...
of position in space, that is,
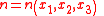 in 3D
in 3DThree-dimensional space
Three-dimensional space is a geometric 3-parameters model of the physical universe in which we live. These three dimensions are commonly called length, width, and depth , although any three directions can be chosen, provided that they do not lie in the same plane.In physics and mathematics, a...
euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. Assuming now that light travels along the x3 axis, the path of a light ray may be parametrized as
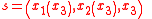 starting at a point
starting at a point 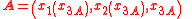 and ending at a point
and ending at a point 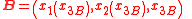 . In this case, when compared to Hamilton's principle above, coordinates
. In this case, when compared to Hamilton's principle above, coordinates 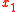 and
and 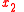 take the role of the generalized coordinates
take the role of the generalized coordinates 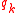 while
while 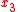 takes the role of parameter
takes the role of parameter  , that is, parameter σ =x3 and N=2.
, that is, parameter σ =x3 and N=2.In the context of calculus of variations
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
this can be written as
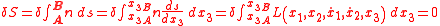
where ds is an infinitesimal displacement along the ray given by
 and
and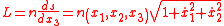
is the optical Lagrangian and
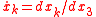 .
.The optical path length
Optical path length
In optics, optical path length or optical distance is the product of the geometric length of the path light follows through the system, and the index of refraction of the medium through which it propagates. A difference in optical path length between two paths is often called the optical path...
(OPL) is defined as
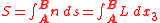
where n is the local refractive index as a function of position along the path between points A and B.
The Euler-Lagrange equations
The general results presented above for Hamilton's principle can be applied to optics using the Lagrangian defined in Fermat's principle. The Euler-Lagrange equations with parameter σ =x3 and N=2 applied to Fermat's principle result in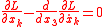
with k=1,2 and where L is the optical Lagrangian and
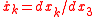 .
.Optical momentum
The optical momentum is defined as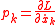
and from the definition of the optical Lagrangian
 this expression can be rewritten as
this expression can be rewritten as
or in vector form
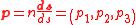
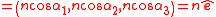
where
 is a unit vector and angles α1, α2 and α3 are the angles p maxes to axis x1, x2 and x3 respectively, as shown in figure "optical momentum". Therefore the optical momentum is a vector of norm
is a unit vector and angles α1, α2 and α3 are the angles p maxes to axis x1, x2 and x3 respectively, as shown in figure "optical momentum". Therefore the optical momentum is a vector of norm
where n is the refractive index at which p is calculated. Vector p points in the direction of propagation of light. If light is propagating in a gradient index optic
Gradient index optics
Gradient-index optics is the branch of optics covering optical effects produced by a gradual variation of the refractive index of a material. Such variations can be used to produce lenses with flat surfaces, or lenses that do not have the aberrations typical of traditional spherical lenses...
the path of the light ray is curved and vector p is tangent to the light ray.
The expression for the optical path length can also be written as a function of the optical momentum. Having in consideration that
 the expression for the optical Lagrangian can be rewritten as
the expression for the optical Lagrangian can be rewritten as
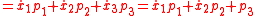
and the expression for the optical path length is

Hamilton's equations
Similarly to what happens in Hamiltonian mechanicsHamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
, also in optics the Hamiltonian is defined by the expression given above for N=2 corresponding to functions
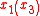 and
and  to be determined
to be determined
Comparing this expression with
 for the Lagrangian results in
for the Lagrangian results in
And the corresponding Hamilton's equations with parameter σ =x3 and k=1,2 applied to optics are
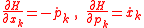
with
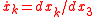 and
and 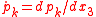 .
.Applications
It is assumed that light travels along the x3 axis, in Hamilton's principle above, coordinates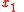 and
and 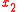 take the role of the generalized coordinates
take the role of the generalized coordinates  while
while 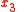 takes the role of parameter
takes the role of parameter  , that is, parameter σ =x3 and N=2.
, that is, parameter σ =x3 and N=2.Refraction and reflection
If plane x1x2 separates two media of refractive index nA below and nB above it, the refractive index is given by a step functionStep function
In mathematics, a function on the real numbers is called a step function if it can be written as a finite linear combination of indicator functions of intervals...

and from Hamilton's equations
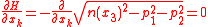
and therefore
 or
or  for k=1,2.
for k=1,2.An incoming light ray has momentum pA before refraction (below plane x1x2) and momentum pB after refraction (above plane x1x2). The light ray makes an angle θA with axis x3 (the normal to the refractive surface) before refraction and an angle θB with axis x3 after refraction. Since the p1 and p2 components of the momentum are constant, only p3 changes from p3A to p3B.
Figure "refraction" shows the geometry of this refraction from which
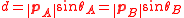 . Since
. Since  and
and  , this last expression can be written as
, this last expression can be written as
which is Snell's law
Snell's law
In optics and physics, Snell's law is a formula used to describe the relationship between the angles of incidence and refraction, when referring to light or other waves passing through a boundary between two different isotropic media, such as water and glass...
of refraction
Refraction
Refraction is the change in direction of a wave due to a change in its speed. It is essentially a surface phenomenon . The phenomenon is mainly in governance to the law of conservation of energy. The proper explanation would be that due to change of medium, the phase velocity of the wave is changed...
.
In figure "refraction", the normal to the refractive surface points in the direction of axis x3, and also of vector
 . A unit normal
. A unit normal 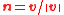 to the refractive surface can then be obtained from the momenta of the incoming and outgoing rays by
to the refractive surface can then be obtained from the momenta of the incoming and outgoing rays by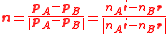
where i and r are a unit vectors in the directions of the incident and refracted rays. Also, the outgoing ray (in the direction of
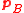 ) is contained in the plane defined by the incoming ray (in the direction of
) is contained in the plane defined by the incoming ray (in the direction of 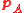 ) and the normal
) and the normal  to the surface.
to the surface.A similar argument can be used for reflection
Reflection (physics)
Reflection is the change in direction of a wavefront at an interface between two differentmedia so that the wavefront returns into the medium from which it originated. Common examples include the reflection of light, sound and water waves...
in deriving the law of specular reflection
Specular reflection
Specular reflection is the mirror-like reflection of light from a surface, in which light from a single incoming direction is reflected into a single outgoing direction...
, only now with nA=nB, resulting in θA=θB. Also, if i and r are unit vectors in the directions of the incident and refracted ray respectively, the corresponding normal to the surface is given by the same expression as for refraction, only with nA=nB

In vector form, if i is a unit vector pointing in the direction of the incident ray and n is the unit normal to the surface, the direction r of the refracted ray is given by:
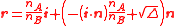
with
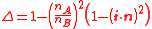
If i·n<0 then -n should be used in the calculations. When
 , light suffers total internal reflection
, light suffers total internal reflectionTotal internal reflection
Total internal reflection is an optical phenomenon that happens when a ray of light strikes a medium boundary at an angle larger than a particular critical angle with respect to the normal to the surface. If the refractive index is lower on the other side of the boundary and the incident angle is...
and the expression for the reflected ray is that of reflection:
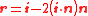
Rays and wavefronts
From the definition of optical path length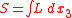
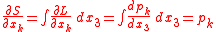
with k=1,2 where the Euler-Lagrange equations
 with k=1,2 were used. Also, from the last of Hamilton's equations
with k=1,2 were used. Also, from the last of Hamilton's equations 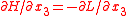 and from
and from  above
above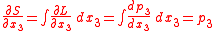
combining the equations for the components of momentum p results in
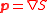
Since p is a vector tangent to the light rays, surfaces S=Constant must be perpendicular to those light rays. These surfaces are called wavefront
Wavefront
In physics, a wavefront is the locus of points having the same phase. Since infrared, optical, x-ray and gamma-ray frequencies are so high, the temporal component of electromagnetic waves is usually ignored at these wavelengths, and it is only the phase of the spatial oscillation that is described...
s. Figure "rays and wavefronts" illustrates this relationship. Also shown is optical momentum p, tangent to a light ray and perpendicular to the wavefront.
Vector field
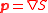 is conservative vector field. The gradient theorem
is conservative vector field. The gradient theoremGradient theorem
The gradient theorem, also known as the fundamental theorem of calculus for line integrals, says that a line integral through a gradient field can be evaluated by evaluating the original scalar field at the endpoints of the curve: \phi\left-\phi\left = \int_L...
can then be applied to the optical path length (as given above) resulting in

and the optical path length S calculated along a curve C between points A and B is a function of only its end points A and B and not the shape of the curve between them. In particular, if the curve is closed, it starts and ends at the same point, or A=B so that
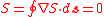
This result may be applied to a closed path ABCDA as in figure "optical path length"
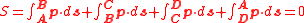
for curve segment AB the optical momentum p is perpendicular to a displacement ds along curve AB, or
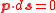 . The same is true for segment CD. For segment BC the optical momentum p has the same direction as displacement ds and
. The same is true for segment CD. For segment BC the optical momentum p has the same direction as displacement ds and 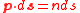 . For segment DA the optical momentum p has the opposite direction to displacement ds and
. For segment DA the optical momentum p has the opposite direction to displacement ds and  . However inverting the direction of the integration so that the integral is taken from A to D, ds inverts direction and
. However inverting the direction of the integration so that the integral is taken from A to D, ds inverts direction and 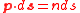 . From these considerations
. From these considerations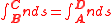
or

and the optical path length SBC between points B and C along the ray connecting them is the same as the optical path length SAD between points A and D along the ray connecting them. The optical path length is constant between wavefronts.
Phase space
Figure "2D phase space" shows at the top some light rays in a two-dimensional space. Here x2=0 and p2=0 so light travels on the plane x1x3 in directions of increasing x3 values. In this case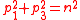 and the direction of a light ray is completely specified by the p1 component of momentum
and the direction of a light ray is completely specified by the p1 component of momentum 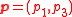 since p2=0. If p1 is given, p3 may be calculated (given the value of the refractive index n) and therefore p1 suffices to determine the direction of the light ray. The refractive index of the medium the ray is traveling in is determined by
since p2=0. If p1 is given, p3 may be calculated (given the value of the refractive index n) and therefore p1 suffices to determine the direction of the light ray. The refractive index of the medium the ray is traveling in is determined by  .
.For example, ray rC crosses axis x1 at coordinate xB with an optical momentum pC, which has its tip on a circle of radius n centered at position xB. Coordinate xB and the horizontal coordinate p1C of momentum pC completely define ray rC as it crosses axis x1. This ray may then be defined by a point rC=(xB,p1C) in space x1p1 as shown at the bottom of the figure. Space x1p1 is called phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
and different light rays may be represented by different points in this space.
As such, ray rD shown at the top is represented by a point rD in phase space at the bottom. All rays crossing axis x1 at coordinate xB contained between rays rC and rD are represented by a vertical line connecting points rC and rD in phase space. Accordingly, all rays crossing axis x1 at coordinate xA contained between rays rA and rB are represented by a vertical line connecting points rA and rB in phase space. In general, all rays crossing axis x1 between xL and xR are represented by a volume R in phase space. The rays at the boundary ∂R of volume R are called edge rays. For example, at position xA of axis x1, rays rA and rB are the edge rays since all other rays are contained between these two.
In three-dimensional geometry the optical momentum is given by
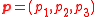 with
with  . If p1 and p2 are given, p3 may be calculated (given the value of the refractive index n) and therefore p1 and p2 suffice to determine the direction of the light ray. A ray traveling along axis x3 is then defined by a point (x1,x2) in plane x1x2 and a direction (p1,p2). It may then be defined by a point in four-dimensional phase space
. If p1 and p2 are given, p3 may be calculated (given the value of the refractive index n) and therefore p1 and p2 suffice to determine the direction of the light ray. A ray traveling along axis x3 is then defined by a point (x1,x2) in plane x1x2 and a direction (p1,p2). It may then be defined by a point in four-dimensional phase spacePhase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
x1x2p1p2.
Conservation of etendue
Figure "volume variation" shows a volume V bound by an area A. Overtime, if the boundary A moves, the volume of V may vary. In particular, an infinitesimal area dA with outward pointing unit normal n moves with a velocity v.This leads to a volume variation
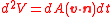 . Making use of Gauss's theorem, the variation in time of the total volume V volume moving in space is
. Making use of Gauss's theorem, the variation in time of the total volume V volume moving in space is
The rightmost term is a volume integral
Volume integral
In mathematics — in particular, in multivariable calculus — a volume integral refers to an integral over a 3-dimensional domain....
over the volume V and the middle term is the surface integral
Surface integral
In mathematics, a surface integral is a definite integral taken over a surface ; it can be thought of as the double integral analog of the line integral...
over the boundary A of the volume V. Also, v is the velocity with which the points in V are moving.
In optics coordinate
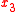 takes the role of time. In phase space a light ray is identified by a point
takes the role of time. In phase space a light ray is identified by a point 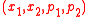 which moves with a "velocity
which moves with a "velocityVelocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
"
 where the dot represents a derivative relative to
where the dot represents a derivative relative to 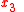 . A set of light rays spreading over
. A set of light rays spreading over 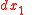 in coordinate
in coordinate 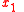 ,
, 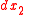 in coordinate
in coordinate 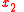 ,
, 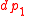 in coordinate
in coordinate 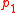 and
and 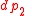 in coordinate
in coordinate  occupies a volume
occupies a volume  in phase space. In general, a large set of rays occupies a large volume
in phase space. In general, a large set of rays occupies a large volume  in phase space to which Gauss's theorem may be applied
in phase space to which Gauss's theorem may be applied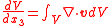
and using Hamilton's equations
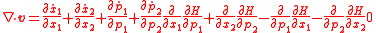
or
 and
and  which means that the phase space volume is conserved as light travels along an optical system.
which means that the phase space volume is conserved as light travels along an optical system.The volume occupied by a set of rays in phase space is called etendue
Etendue
Etendue or étendue is a property of pencils of rays in an optical system, which characterizes how "spread out" light is in area and angle. It may also be seen as a volume in phase space....
, which is conserved as light rays progress in the optical system along direction x3. This corresponds to Liouville's theorem
Liouville's theorem (Hamiltonian)
In physics, Liouville's theorem, named after the French mathematician Joseph Liouville, is a key theorem in classical statistical and Hamiltonian mechanics...
, which also applies to Hamiltonian mechanics
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
.
Imaging and nonimaging optics
Figure "conservation of etendue" shows on the left a diagrammatic two-dimensional optical system in which x2=0 and p2=0 so light travels on the plane x1x3 in directions of increasing x3 values.Light rays crossing the input aperture of the optic at point x1=xI are contained between edge rays rA and rB represented by a vertical line between points rA and rB at the phase space of the input aperture (right, bottom corner of the figure). All rays crossing the input aperture are represented in phase space by a region RI.
Also, light rays crossing the output aperture of the optic at point x1=xO are contained between edge rays rA and rB represented by a vertical line between points rA and rB at the phase space of the output aperture (right, top corner of the figure). All rays crossing the output aperture are represented in phase space by a region RO.
Conservation of etendue in the optical system means that the volume (or area in this two-dimensional case) in phase space occupied by RI at the input aperture must be the same as the volume in phase space occupied by RO at the output aperture.
In imaging optics, all light rays crossing the input aperture at x1=xI are redirected by it towards the output aperture at x1=xO where xI=m xO. This ensures that an image of the input of formed at the output with a magnification m. In phase space, this means that vertical lines in the phase space at the input are transformed into vertical lines at the output. That would be the case of vertical line rA rB in RI transformed to vertical line rA rB in RO.
In nonimaging optics
Nonimaging optics
Nonimaging optics is the branch of optics concerned with the optimal transfer of light radiation between a source and a target...
, the goal is not to form an image but simply to transfer all light from the input aperture to the output aperture. This is accomplished by transforming the edge rays ∂RI of RI to edge rays ∂RO of RO. This is known as the edge ray principle.
Generalizations
Above it was assumed that light travels along the x3 axis, in Hamilton's principle above, coordinates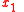 and
and 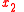 take the role of the generalized coordinates
take the role of the generalized coordinates 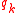 while
while 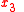 takes the role of parameter
takes the role of parameter  , that is, parameter σ =x3 and N=2. However, different parametrizations of the light rays are possible, as well as the use of generalized coordinates
, that is, parameter σ =x3 and N=2. However, different parametrizations of the light rays are possible, as well as the use of generalized coordinatesGeneralized coordinates
In the study of multibody systems, generalized coordinates are a set of coordinates used to describe the configuration of a system relative to some reference configuration....
.
General ray parametrization
A more general situation can be considered in which the path of a light ray is parametrized as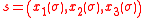 in which σ is a general parameter. In this case, when compared to Hamilton's principle above, coordinates
in which σ is a general parameter. In this case, when compared to Hamilton's principle above, coordinates  ,
, 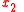 and
and 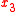 take the role of the generalized coordinates
take the role of the generalized coordinates 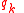 with N=3. Applying Hamilton's principle to optics in this case leads to
with N=3. Applying Hamilton's principle to optics in this case leads to
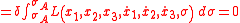
where now
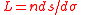 and
and 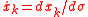 and for which the Euler-Lagrange equations applied to this form of Fermat's principle result in
and for which the Euler-Lagrange equations applied to this form of Fermat's principle result in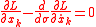
with k=1,2,3 and where L is the optical Lagrangian. Also in this case the optical momentum is defined as

and the Hamiltonian P is defined by the expression given above for N=3 corresponding to functions
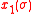 ,
, 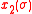 and
and 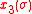 to be determined
to be determined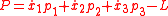
And the corresponding Hamilton's equations with k=1,2,3 applied optics are

with
 and
and 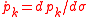 .
.The optical Lagrangian is given by

and does not explicitly depend on parameter σ. For that reason not all solutions of the Euler-Lagrange equations will be possible light rays, since their derivation assumed an explicit dependence of L on σ which does not happen in optics.
The optical momentum components can be obtained from

where
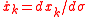 . The expression for the Lagrangian can be rewritten as
. The expression for the Lagrangian can be rewritten as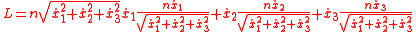

Comparing this expression for L with that for the Hamiltonian P it can be concluded that

From the expressions for the components
 of the optical momentum results
of the optical momentum results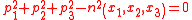
The optical Hamiltonian is chosen as

although other choices could be made. The Hamilton's equations with k=1,2,3 defined above together with
 define the possible light rays.
define the possible light rays.Generalized coordinates
As in Hamiltonian mechanicsHamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
, it is also possible to write the equations of Hamiltonian optics in terms of generalized coordinates
Generalized coordinates
In the study of multibody systems, generalized coordinates are a set of coordinates used to describe the configuration of a system relative to some reference configuration....
 , generalized momenta
, generalized momenta 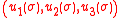 and Hamiltonian P as
and Hamiltonian P as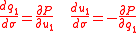
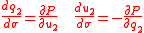
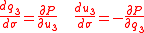
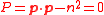
where the optical momentum is given by
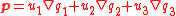


and
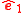 ,
,  and
and  are unit vectors. A particular case is obtained when these vectors form a orthonormal basis
are unit vectors. A particular case is obtained when these vectors form a orthonormal basisOrthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
, that is, they are all perpendicular to each other. In that case,
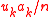 is the cosine of the angle the optical momentum
is the cosine of the angle the optical momentum 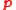 makes to unit vector
makes to unit vector  .
.See also
- Hamiltonian mechanicsHamiltonian mechanicsHamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
- Calculus of variations

