In differential geometry, the jet bundle is a certain construction which makes a new smooth fiber bundle

Fiber bundle

In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...

 out of a given smooth fiber bundle. It makes it possible to write differential equation

Differential equation

A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...

s on sections of a fiber bundle in an invariant form. Jets may also be seen as the coordinate free versions of taylor expansions.

Historically, jet bundles are attributed to Ehresmann, and were an advance on the method (prolongation) of Élie Cartan

Élie Cartan

Élie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...

, of dealing geometrically with higher derivatives

Derivative

In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...

, by imposing differential form

Differential form

In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...

 conditions on newly-introduced formal variables. Jet bundles are sometimes called sprays, although sprays

Spray (mathematics)

In differential geometry, a spray is a vector field H on the tangent bundle TM that encodes a quasilinear second order system of ordinary differential equations on the base manifold M. Usually a spray is required to be homogeneous in the sense that its integral curves t→ΦHt∈TM obey the rule...

 usually refer more specifically to the associated vector field induced on the corresponding bundle (e.g., the geodesic spray on Finsler manifold

Finsler manifold

In mathematics, particularly differential geometry, a Finsler manifold is a differentiable manifold together with the structure of an intrinsic quasimetric space in which the length of any rectifiable curve is given by the length functional...

s.)

More recently, jet bundles have appeared as a concise way to describe phenomena associated with the derivatives of maps, particularly those associated with the calculus of variations

Calculus of variations

Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...

. Consequently, the jet bundle is now recognized as the correct domain for a geometrical covariant field theory

Covariant classical field theory

In recent years, there has been renewed interest in covariant classical field theory. Here, classical fields are represented by sections of fiber bundles and their dynamics is phrased in the context of a finite-dimensional space of fields. Nowadays, it is well known that jet bundles and the...

 and much work is done in general relativistic

General relativity

General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...

 formulations of fields using this approach.

Jets

Let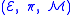 be a fiber bundle

Fiber bundle

In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...

 in a category of manifold

Manifold

In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....

s and let 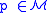, with .
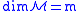Let 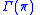denote the set of all local sections whose domain contains . Let 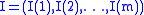be a multi-index (an ordered -tuple of integers), then



Define the local sections 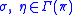to have the same -jet at if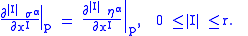


The relation that two maps have the same -jet is an equivalence relation

Equivalence relation

In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...

. An r-jet is an equivalence class under this relation, and the r-jet with representative is denoted 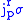. The integer is also called the order of the jet.

is the source of .

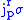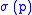is the target of .

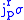Jet manifolds

The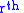 jet manifold of is the set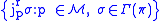


and is denoted 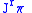. We may define projections 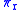and 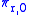called the source and target projections respectively, by


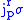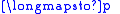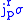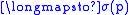If 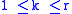, then the 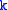-jet projection is the function 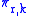defined by


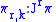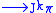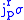From this definition, it is clear that and that if 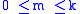, then . It is conventional to regard 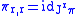, the identity map

Identity function

In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...

 on 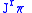and to identify 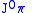with .

The functions 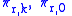and are smooth

Smooth

Smooth means having a texture that lacks friction. Not rough.Smooth may also refer to:-In mathematics:* Smooth function, a function that is infinitely differentiable; used in calculus and topology...

 surjective submersion

Submersion (mathematics)

In mathematics, a submersion is a differentiable map between differentiable manifolds whose differential is everywhere surjective. This is a basic concept in differential topology...

s.
A coordinate system

Coordinate system

In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...

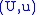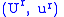 on will generate a coordinate system on . Let be an adapted coordinate chart on , where . The induced coordinate chart on 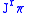is defined by


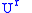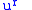where


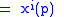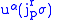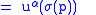and the 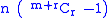functions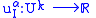


are specified by


and are known as the derivative coordinates.

Given an atlas of adapted charts 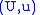on , the corresponding collection of charts 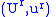is a finite-dimensional  atlas on .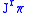

Jet bundles

Since the atlas on each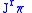 defines a manifold, the triples 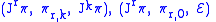and 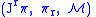all define fibered manifolds.
In particular, if is a fiber bundle, the triple defines the 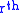jet bundle of .

If is an open submanifold, then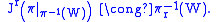


If 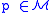, then the fiber 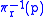is denoted .

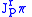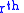Let be a local section of with domain . The jet prolongation of is the map defined by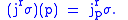


Note that , so 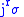really is a section. In local coordinates, 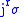is given by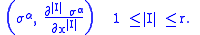


We identify 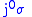with .

Example

If is the trivial bundle 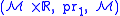, then there is a canonical diffeomorphism

Diffeomorphism

In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...

 between the first jet bundle 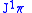and .
To construct this diffeomorphism, for each 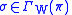write .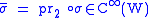

Then, whenever


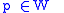
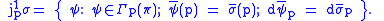
Consequently, the mapping


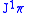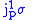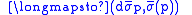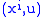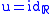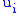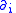is well-defined and is clearly injective. Writing it out in coordinates shows that it is a diffeomorphism, because if are coordinates on , where is the identity coordinate, then the derivative coordinates on correspond to the coordinates on .

Likewise, if is the trivial bundle 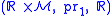, then there exists a canonical diffeomorphism between 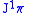and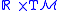

Contact forms

A differential 1-form  on the space 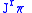is called a contact form (i.e. 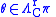) if it is pulled back to the zero form on by all prolongations.
In other words, if 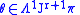, then 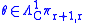if and only if

If and only if

In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....

, for every open submanifold and every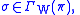


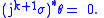
The distribution

Distribution (differential geometry)

In differential geometry, a discipline within mathematics, a distribution is a subset of the tangent bundle of a manifold satisfying certain properties...

 on 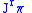generated by the contact forms is called the Cartan distribution. It is the main geometrical structure on jet spaces and plays an important role in the geometric theory of partial differential equation

Partial differential equation

In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...

s. The Cartan distributions are not involutive

Distribution (differential geometry)

In differential geometry, a discipline within mathematics, a distribution is a subset of the tangent bundle of a manifold satisfying certain properties...

 and are of growing dimension when passing to higher order jet spaces. Surprisingly though, when passing to the space of infinite order jets 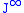this distribution is involutive and finite dimensional. Its dimension coinciding with the dimension of the base manifold .

Example

Let us consider the case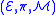 , where and .
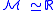Then, 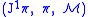defines the first jet bundle, and may be coordinated by 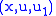, where


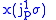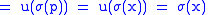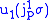for all 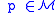and 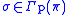. A general 1-form on 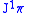takes the form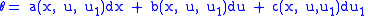


A section 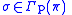has first prolongation .
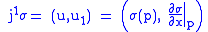Hence, 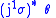can be calculated as


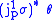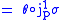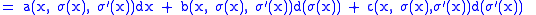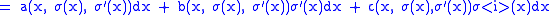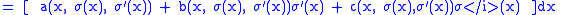This will vanish for all sections if and only if 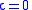and 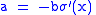. Hence, must necessarily be a multiple of the basic contact form .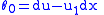
Proceeding to the second jet space with additional coordinate , such that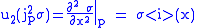


a general 1-form has the construction


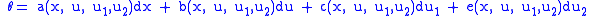
This is a contact form if and only if

If and only if

In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....

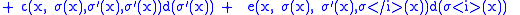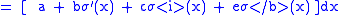which implies that 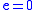and 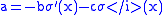. Therefore, is a contact form if and only if


where 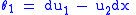is the next basic contact form
(Note that here we are identifying the form 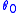with its pull-back 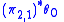to ).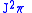

In general, providing 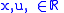, a contact form on can be written as a linear combination

Linear combination

In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...

 of the basic contact forms


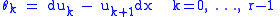
where .

Similar arguments lead to a complete characterization of all contact forms.

In local coordinates, every contact one-form on 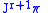can be written as a linear combination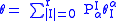


with smooth coefficients 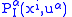of the basic contact forms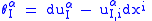


is known as the order of the contact form . Note that contact forms on 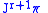have orders at most .
Contact forms provide a characterization of those local sections of 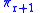which are prolongations of sections of .

Let 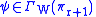, then 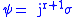where 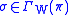if and only if

Vector fields

A general vector field

Vector field

In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...

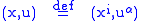 on the total space , coordinated by , is


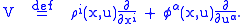
A vector field is called horizontal, meaning all the vertical coefficients vanish, if .

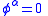A vector field is called vertical, meaning all the horizontal coefficients vanish, if .

For fixed , we identify


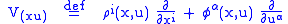
having coordinates 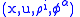, with an element in the fiber of over 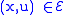, called a tangent vector

Tangent vector

A tangent vector is a vector that is tangent to a curve or surface at a given point.Tangent vectors are described in the differential geometry of curves in the context of curves in Rn. More generally, tangent vectors are elements of a tangent space of a differentiable manifold....

 in . A section


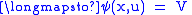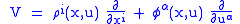is called a vector field on with and .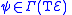

The jet bundle 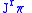is coordinated by 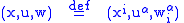. For fixed , identify


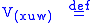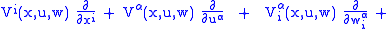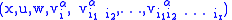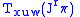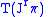having coordinates , with an element in the fiber of over 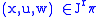, called a tangent vector in .
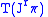Here, are real-valued functions on 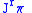. A section


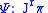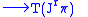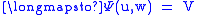is a vector field on 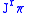, and we say .

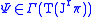Partial differential equations

Let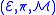 be a fiber bundle. An 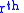order partial differential equation

Partial differential equation

In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...

on is a closed

Closed

Closed may refer to:Math* Closure * Closed manifold* Closed orbits* Closed set* Closed differential form* Closed map, a function that is closed.Other* Cloister, a closed walkway* Closed-circuit television...

 embedded

Embedding

In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....

 submanifold 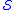of the jet manifold .
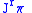A solution is a local section 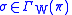satisfying .

Let us consider an example of a first order partial differential equation.

Example

Let be the trivial bundle with global coordinates .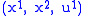
Then the map 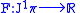defined by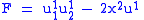


gives rise to the differential equation


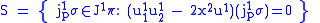
which can be written


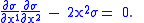
The particular section defined by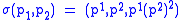


has first prolongation given by


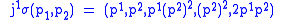
and is a solution of this differential equation, because


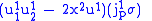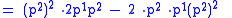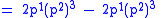and so 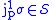for every .

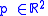Jet Prolongation

A local diffeomorphism defines a contact transformation of order if it preserves the contact ideal, meaning that if is any contact form on 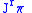, then 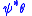is also a contact form.

The flow generated by a vector field 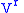on the jet space 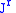forms a one-parameter group of contact transformations if and only if the Lie derivative

Lie derivative

In mathematics, the Lie derivative , named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a vector field or more generally a tensor field, along the flow of another vector field...

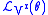  of any contact form preserves the contact ideal.

Let us begin with the first order case. Consider a general vector field 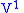on 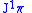, given by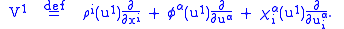


We now apply 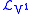to the basic contact forms 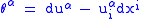, and obtain


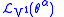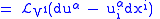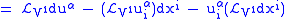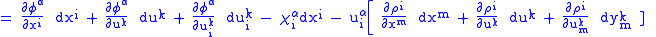where we have expanded the exterior derivative

Exterior derivative

In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....

 of the functions in terms of their coordinates.
Next, we note that


and so we may write


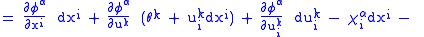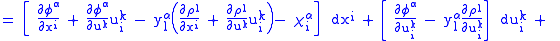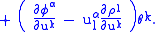Therefore, 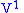determines a contact transformation if and only if the coefficients of and in the formula vanish.
The latter requirements imply the contact conditions


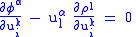
The former requirements provide explicit formulae for the coefficients of the first derivative terms in :
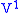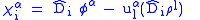where

denotes the zeroth order truncation of the total derivative .

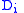Thus, the contact conditions uniquely prescribe the prolongation of any point or contact vector field. That is, if 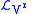satisfies these equations, 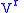is called the 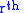prolongation of 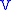to a vector field on .

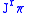These results are best understood when applied to a particular example. Hence, let us examine the following.

Example

Let us consider the case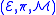 , where and .
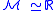Then, 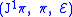defines the first jet bundle, and may be coordinated by 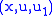, where


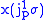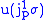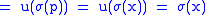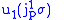for all 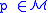and 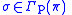. A contact form on 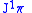has the form


Let us consider a vector 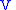on , having the form


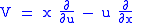
Then, the first prolongation of this vector field to is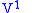


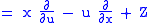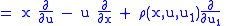If we now take the Lie derivative of the contact form with respect to this prolonged vector field, 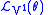, we obtain


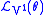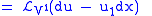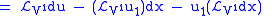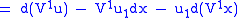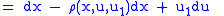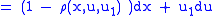But, we may identify 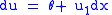. Thus, we get


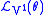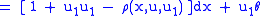Hence, for 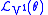to preserve the contact ideal, we require


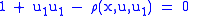And so the first prolongation of 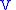to a vector field on is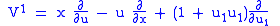


Let us also calculate the second prolongation of 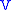to a vector field on .
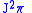We have 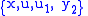as coordinates on 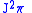. Hence, the prolonged vector has the form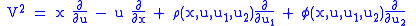


The contacts forms are


To preserve the contact ideal, we require


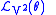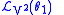Now, has no 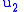dependency. Hence, from this equation we will pick up the formula for , which will necessarily be the same result as we found for 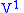. Therefore, the problem is analogous to prolonging the vector field 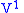to .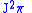
That is to say, we may generate the 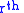-prolongation of a vector field by recursively applying the Lie derivative of the contact forms with respect to the prolonged vector fields, times.
So, we have


and so


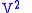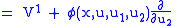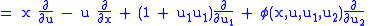Therefore, the Lie derivative of the second contact form with respect to 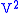is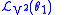


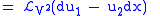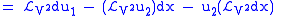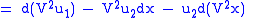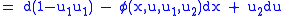Again, let us identify and . Then we have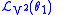


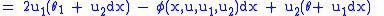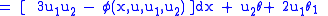Hence, for 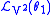to preserve the contact ideal, we require


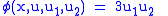And so the second prolongation of 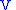to a vector field on 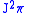is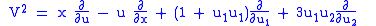


Note that the first prolongation of 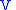can be recovered by omitting the second derivative terms in , or by projecting back to .

Infinite Jet Spaces

The inverse limit

Inverse limit

In mathematics, the inverse limit is a construction which allows one to "glue together" several related objects, the precise manner of the gluing process being specified by morphisms between the objects...

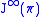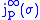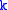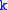 of the sequence of projections gives rise to the infinite jet space . A point is the equivalence class of sections of that have the same -jet in as for all values of . The natural projection maps 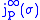into .

Just by thinking in terms of coordinates, 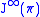appears to be an infinite-dimensional geometric object. In fact, the simplest way of introducing a differentiable structure on 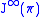, not relying on differentiable charts, is given by the differential calculus over commutative algebras

Differential calculus over commutative algebras

In mathematics the differential calculus over commutative algebras is a part of commutative algebra based on the observation that most concepts known from classical differential calculus can be formulated in purely algebraic terms...

. Dual to the sequence of projections 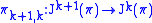of manifolds is the sequence of injections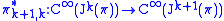

of commutative algebras. Let's denote 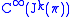simply by . Take now the direct limit

Direct limit

In mathematics, a direct limit is a colimit of a "directed family of objects". We will first give the definition for algebraic structures like groups and modules, and then the general definition which can be used in any category.- Algebraic objects :In this section objects are understood to be...

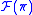  of the 's. It will be a commutative algebra, which can be assumed to be the smooth functions algebra over the geometric object . Observe that 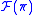, being born as a direct limit, carries an additional structure: it is a filtered commutative algebra.

Roughly speaking, a concrete element will always belong to some 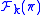, so it is a smooth function on the finite-dimensional manifold 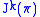in the usual sense.

Infinitely prolonged PDE's

Given a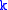 -th order system of PDE's 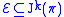, the collection 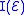of vanishing on smooth functions on 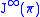is an ideal

Ideal

-In philosophy:* Ideal , values that one actively pursues as goals* Platonic ideal, a philosophical idea of trueness of form, associated with Plato-In mathematics:* Ideal , special subsets of a ring considered in abstract algebra...

 in the algebra , and hence in the direct limit 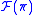too.

Enhance 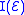by adding all the possible compositions of total derivative

Total derivative

In the mathematical field of differential calculus, the term total derivative has a number of closely related meanings.The total derivative of a function f, of several variables, e.g., t, x, y, etc., with respect to one of its input variables, e.g., t, is different from the partial derivative...

s applied to all its elements. This way we get a new ideal 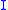of 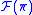which is now closed under the operation of taking total derivative. The submanifold of cut out by 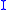is called the infinite prolongation of .

Geometrically, 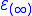is the manifold of formal solutions of . A point 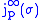of 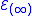can be easily seen to be represented by a section whose 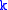-jet's graph is tangent to at the point 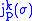with arbitrarily high order of tangency.

Analytically, if is given by , a formal solution can be understood as the set of Taylor coefficients of a section in a point that make vanish the Taylor series

Taylor series

In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....

 of 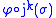at the point .

Most importantly, the closure properties of 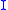imply that 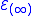is tangent to the infinite-order contact structure on , so that by restricting to 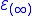one gets the diffiety

Diffiety

In mathematics a diffiety, is a geometrical object introduced by playing the same role in the modern theory of partial differential equations as algebraic varieties play for algebraic equations....

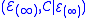 , and can study the associated C-spectral sequence.

Remark

This article has defined jets of local sections of a bundle, but it is possible to define jets of functions , where and are manifolds; the jet of then just corresponds to the jet of the section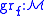


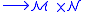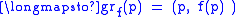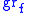( is known as the graph of the function ) of the trivial bundle 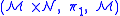. However, this restriction does not simplify the theory, as the global triviality of does not imply the global triviality of 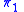.