
Canonical transformation
Encyclopedia
In Hamiltonian mechanics
, a canonical transformation is a change of canonical coordinates
(q,p,t) → (Q,P,t) that preserves the form of Hamilton's equations (that is, the new Hamilton equations that result from the new Hamiltonian constructed by transformation may be simply obtained by substituting the old variables by the new ones), although it might not preserve the Hamiltonian
itself. This is sometimes known as form invariance. Canonical transformations are useful in their own right, and also form the basis for the Hamilton–Jacobi equation
s (a useful method for calculating conserved quantities
) and Liouville's theorem
(itself the basis for classical statistical mechanics
).
Since Lagrangian mechanics
is based on generalized coordinates
, transformations of the coordinates q → Q do not affect the form of Lagrange's equations
and, hence, do not affect the form of Hamilton's equations if we simultaneously change the momentum by a Legendre transform into
Therefore, coordinate transformations (also called point transformations) are a type of canonical transformation. However, the class of canonical transformations is much broader, since the old generalized coordinates, momenta and even time may be combined to form the new generalized coordinates and momenta. Canonical transformations that do not include the time explicitly are called restricted canonical transformations (many textbooks consider only this type).
For clarity, we restrict the presentation here to calculus
and classical mechanics
. Readers familiar with more advanced mathematics such as cotangent bundle
s, exterior derivative
s and symplectic manifold
s should read the related symplectomorphism
article. (Canonical transformations are a special case of a symplectomorphism.) However, a brief introduction to the modern mathematical description is included at the end of this article.
 represent a list of
represent a list of
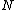 generalized coordinates
generalized coordinates
, e.g.,

that need not transform like a vector under rotation
. As usual, a dot over a variable or list signifies the time derivative, e.g.,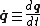 . The dot product
. The dot product
notation between two lists of the same number of coordinates is a shorthand for the sum of the products of corresponding components, e.g.,

The dot product (also known as an "inner product") maps the two coordinate lists into one variable representing a single numerical value.

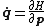
By definition, the transformed coordinates have analogous dynamics
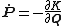
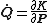
where K(Q,P) is a new Hamiltonian that must be determined.
In general, a transformation (q,p,t) → (Q,P,t) does not preserve the form of Hamilton's equations. For time independent transformations between (q,p) and (Q,P) we may check if the transformation is restricted canonical, as follows. Since restricted transformations have no explicit time dependence (by construction), the time derivative of a new generalized coordinate Qm is
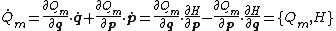
where is the Poisson bracket
is the Poisson bracket
.
We also have the identity for the conjugate momentum Pm

If the transformation is canonical, these two must be equal, resulting in the equations
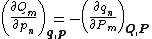
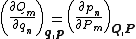
The analogous argument for the generalized momenta Pm leads to two other sets of equations
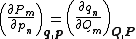
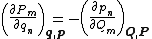
These are the direct conditions to check whether a given transformation is canonical.
, which states that the volume in phase space is conserved under canonical transformations, i.e.,
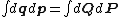
By calculus
, the latter integral must equal the former times the Jacobian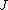
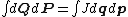
where the Jacobian is the determinant
of the matrix
of partial derivative
s, which we write as
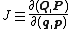
Exploiting the "division" property of Jacobians yields

Eliminating the repeated variables gives
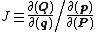
Application of the direct conditions above yields .
.
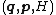 and
and 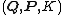 , we may resort to an indirect generating function approach. Both sets of variables must obey Hamilton's principle
, we may resort to an indirect generating function approach. Both sets of variables must obey Hamilton's principle


To satisfy both variational integrals
, we must have
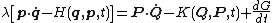
In general, the scaling factor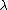 is set equal to one; canonical transformations for which
is set equal to one; canonical transformations for which  are called extended canonical transformations.
are called extended canonical transformations.
Here is a generating function
is a generating function
of one old canonical coordinate
( or
or  ), one new canonical coordinate
), one new canonical coordinate
(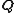 or
or 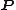 ) and (possibly) the time
) and (possibly) the time  . Thus, there are four basic types of generating functions, depending on the choice of variables.
. Thus, there are four basic types of generating functions, depending on the choice of variables.
As will be shown below, the generating function will define a transformation from old to new canonical coordinates
, and any such transformation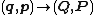 is guaranteed to be canonical.
is guaranteed to be canonical.
 depends only on the old and new generalized coordinates
depends only on the old and new generalized coordinates
To derive the implicit transformation, we expand the defining equation above
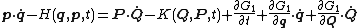
Since the new and old coordinates are each independent, the following equations must hold
equations must hold


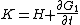
These equations define the transformation as follows. The first set of
as follows. The first set of  equations
equations

define relations between the new generalized coordinates
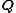 and the old canonical coordinates
and the old canonical coordinates
 . Ideally, one can invert these relations to obtain formulae for each
. Ideally, one can invert these relations to obtain formulae for each 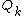 as a function of the old canonical coordinates. Substitution of these formulae for the
as a function of the old canonical coordinates. Substitution of these formulae for the 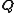 coordinates into the second set of
coordinates into the second set of 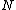 equations
equations
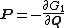
yields analogous formulae for the new generalized momenta in terms of the old canonical coordinates
in terms of the old canonical coordinates
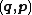 . We then invert both sets of formulae to obtain the old canonical coordinates
. We then invert both sets of formulae to obtain the old canonical coordinates
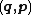 as functions of the new canonical coordinates
as functions of the new canonical coordinates
 . Substitution of the inverted formulae into the final equation
. Substitution of the inverted formulae into the final equation
yields a formula for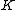 as a function of the new canonical coordinates
as a function of the new canonical coordinates
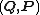 .
.
In practice, this procedure is easier than it sounds, because the generating function is usually simple. For example, let
This results in swapping the generalized coordinates for the momenta and vice versa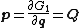

and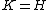 . This example illustrates how independent the coordinates and momenta are in the Hamiltonian formulation; they're equivalent variables.
. This example illustrates how independent the coordinates and momenta are in the Hamiltonian formulation; they're equivalent variables.
 depends only on the old generalized coordinates
depends only on the old generalized coordinates
and the new generalized momenta
where the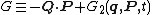 terms represent a Legendre transformation
terms represent a Legendre transformation
to change the right-hand side of the equation below. To derive the implicit transformation, we expand the defining equation above

Since the old coordinates and new momenta are each independent, the following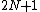 equations must hold
equations must hold
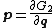
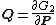

These equations define the transformation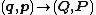 as follows. The first set of
as follows. The first set of  equations
equations
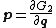
define relations between the new generalized momenta and the old canonical coordinates
and the old canonical coordinates
 . Ideally, one can invert these relations to obtain formulae for each
. Ideally, one can invert these relations to obtain formulae for each 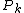 as a function of the old canonical coordinates. Substitution of these formulae for the
as a function of the old canonical coordinates. Substitution of these formulae for the 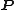 coordinates into the second set of
coordinates into the second set of 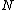 equations
equations

yields analogous formulae for the new generalized coordinates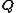 in terms of the old canonical coordinates
in terms of the old canonical coordinates
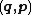 . We then invert both sets of formulae to obtain the old canonical coordinates
. We then invert both sets of formulae to obtain the old canonical coordinates
 as functions of the new canonical coordinates
as functions of the new canonical coordinates
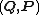 . Substitution of the inverted formulae into the final equation
. Substitution of the inverted formulae into the final equation
yields a formula for as a function of the new canonical coordinates
as a function of the new canonical coordinates
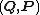 .
.
In practice, this procedure is easier than it sounds, because the generating function is usually simple. For example, let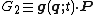
where is a set of
is a set of  functions.
functions.
This results in a point transformation of the generalized coordinates
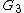 depends only on the old generalized momenta and the new generalized coordinates
depends only on the old generalized momenta and the new generalized coordinates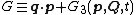
where the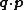 terms represent a Legendre transformation
terms represent a Legendre transformation
to change the left-hand side of the equation below. To derive the implicit transformation, we expand the defining equation above
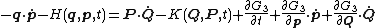
Since the new and old coordinates are each independent, the following equations must hold
equations must hold
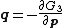

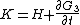
These equations define the transformation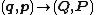 as follows. The first set of
as follows. The first set of 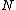 equations
equations

define relations between the new generalized coordinates
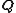 and the old canonical coordinates
and the old canonical coordinates
 . Ideally, one can invert these relations to obtain formulae for each
. Ideally, one can invert these relations to obtain formulae for each 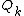 as a function of the old canonical coordinates. Substitution of these formulae for the
as a function of the old canonical coordinates. Substitution of these formulae for the  coordinates into the second set of
coordinates into the second set of 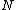 equations
equations
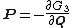
yields analogous formulae for the new generalized momenta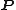 in terms of the old canonical coordinates
in terms of the old canonical coordinates
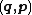 . We then invert both sets of formulae to obtain the old canonical coordinates
. We then invert both sets of formulae to obtain the old canonical coordinates
 as functions of the new canonical coordinates
as functions of the new canonical coordinates
 . Substitution of the inverted formulae into the final equation
. Substitution of the inverted formulae into the final equation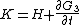
yields a formula for as a function of the new canonical coordinates
as a function of the new canonical coordinates
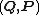 .
.
In practice, this procedure is easier than it sounds, because the generating function is usually simple.
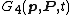 depends only on the old and new generalized momenta
depends only on the old and new generalized momenta
where the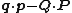 terms represent a Legendre transformation
terms represent a Legendre transformation
to change both sides of the equation below. To derive the implicit transformation, we expand the defining equation above

Since the new and old coordinates are each independent, the following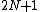 equations must hold
equations must hold
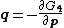
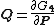
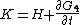
These equations define the transformation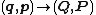 as follows. The first set of
as follows. The first set of 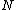 equations
equations

define relations between the new generalized momenta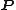 and the old canonical coordinates
and the old canonical coordinates
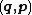 . Ideally, one can invert these relations to obtain formulae for each
. Ideally, one can invert these relations to obtain formulae for each 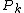 as a function of the old canonical coordinates. Substitution of these formulae for the
as a function of the old canonical coordinates. Substitution of these formulae for the 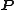 coordinates into the second set of
coordinates into the second set of 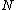 equations
equations
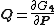
yields analogous formulae for the new generalized coordinates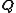 in terms of the old canonical coordinates
in terms of the old canonical coordinates
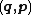 . We then invert both sets of formulae to obtain the old canonical coordinates
. We then invert both sets of formulae to obtain the old canonical coordinates
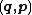 as functions of the new canonical coordinates
as functions of the new canonical coordinates
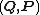 . Substitution of the inverted formulae into the final equation
. Substitution of the inverted formulae into the final equation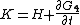
yields a formula for as a function of the new canonical coordinates
as a function of the new canonical coordinates
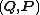 .
.
 and
and 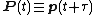 , then Hamilton's principle
, then Hamilton's principle
is automatically satisfied
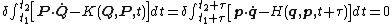
since a valid trajectory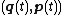 should always satisfy Hamilton's principle
should always satisfy Hamilton's principle
, regardless of the endpoints.
are any coordinates on the phase space (cotangent bundle
) of the system that allow the canonical one-form to be written as
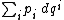
up to a total differential (exact form). The change of variable between one set of canonical coordinates and another is a canonical transformation. The index of the generalized coordinates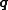 is written here as a superscript (
is written here as a superscript (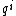 ), not as a subscript as done above (
), not as a subscript as done above (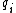 ). The superscript conveys the contravariant transformation properties
). The superscript conveys the contravariant transformation properties
of the generalized coordinates, and does not mean that the coordinate is being raised to a power. Further details may be found at the symplectomorphism
article.
, in the study of the Earth-Moon-Sun system. This work resulted in the publication of a pair of large volumes as Mémoires by the French Academy of Sciences
, in 1860 and 1867.
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
, a canonical transformation is a change of canonical coordinates
Canonical coordinates
In mathematics and classical mechanics, canonical coordinates are particular sets of coordinates on the phase space, or equivalently, on the cotangent manifold of a manifold. Canonical coordinates arise naturally in physics in the study of Hamiltonian mechanics...
(q,p,t) → (Q,P,t) that preserves the form of Hamilton's equations (that is, the new Hamilton equations that result from the new Hamiltonian constructed by transformation may be simply obtained by substituting the old variables by the new ones), although it might not preserve the Hamiltonian
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
itself. This is sometimes known as form invariance. Canonical transformations are useful in their own right, and also form the basis for the Hamilton–Jacobi equation
Hamilton–Jacobi equation
In mathematics, the Hamilton–Jacobi equation is a necessary condition describing extremal geometry in generalizations of problems from the calculus of variations. In physics, the Hamilton–Jacobi equation is a reformulation of classical mechanics and, thus, equivalent to other formulations such as...
s (a useful method for calculating conserved quantities
Constant of motion
In mechanics, a constant of motion is a quantity that is conserved throughout the motion, imposing in effect a constraint on the motion. However, it is a mathematical constraint, the natural consequence of the equations of motion, rather than a physical constraint...
) and Liouville's theorem
Liouville's theorem (Hamiltonian)
In physics, Liouville's theorem, named after the French mathematician Joseph Liouville, is a key theorem in classical statistical and Hamiltonian mechanics...
(itself the basis for classical statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
).
Since Lagrangian mechanics
Lagrangian mechanics
Lagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
is based on generalized coordinates
Generalized coordinates
In the study of multibody systems, generalized coordinates are a set of coordinates used to describe the configuration of a system relative to some reference configuration....
, transformations of the coordinates q → Q do not affect the form of Lagrange's equations
Lagrangian mechanics
Lagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
and, hence, do not affect the form of Hamilton's equations if we simultaneously change the momentum by a Legendre transform into

Therefore, coordinate transformations (also called point transformations) are a type of canonical transformation. However, the class of canonical transformations is much broader, since the old generalized coordinates, momenta and even time may be combined to form the new generalized coordinates and momenta. Canonical transformations that do not include the time explicitly are called restricted canonical transformations (many textbooks consider only this type).
For clarity, we restrict the presentation here to calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
and classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
. Readers familiar with more advanced mathematics such as cotangent bundle
Cotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
s, exterior derivative
Exterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
s and symplectic manifold
Symplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
s should read the related symplectomorphism
Symplectomorphism
In mathematics, a symplectomorphism is an isomorphism in the category of symplectic manifolds.-Formal definition:A diffeomorphism between two symplectic manifolds f: \rightarrow is called symplectomorphism, iff^*\omega'=\omega,...
article. (Canonical transformations are a special case of a symplectomorphism.) However, a brief introduction to the modern mathematical description is included at the end of this article.
Notation
Boldface variables such as represent a list of
represent a list of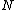 generalized coordinates
generalized coordinatesGeneralized coordinates
In the study of multibody systems, generalized coordinates are a set of coordinates used to describe the configuration of a system relative to some reference configuration....
, e.g.,

that need not transform like a vector under rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
. As usual, a dot over a variable or list signifies the time derivative, e.g.,
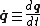 . The dot product
. The dot productDot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
notation between two lists of the same number of coordinates is a shorthand for the sum of the products of corresponding components, e.g.,

The dot product (also known as an "inner product") maps the two coordinate lists into one variable representing a single numerical value.
Direct approach
The functional form of Hamilton's equations is
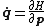
By definition, the transformed coordinates have analogous dynamics
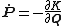
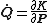
where K(Q,P) is a new Hamiltonian that must be determined.
In general, a transformation (q,p,t) → (Q,P,t) does not preserve the form of Hamilton's equations. For time independent transformations between (q,p) and (Q,P) we may check if the transformation is restricted canonical, as follows. Since restricted transformations have no explicit time dependence (by construction), the time derivative of a new generalized coordinate Qm is
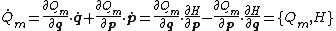
where
 is the Poisson bracket
is the Poisson bracketPoisson bracket
In mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time-evolution of a Hamiltonian dynamical system...
.
We also have the identity for the conjugate momentum Pm

If the transformation is canonical, these two must be equal, resulting in the equations
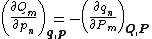
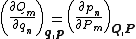
The analogous argument for the generalized momenta Pm leads to two other sets of equations
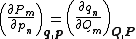
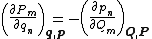
These are the direct conditions to check whether a given transformation is canonical.
Liouville's theorem
The direct conditions allow us to prove Liouville's theoremLiouville's theorem (Hamiltonian)
In physics, Liouville's theorem, named after the French mathematician Joseph Liouville, is a key theorem in classical statistical and Hamiltonian mechanics...
, which states that the volume in phase space is conserved under canonical transformations, i.e.,
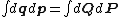
By calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
, the latter integral must equal the former times the Jacobian
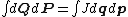
where the Jacobian is the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
of partial derivative
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s, which we write as
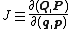
Exploiting the "division" property of Jacobians yields

Eliminating the repeated variables gives
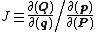
Application of the direct conditions above yields
 .
.Generating function approach
To guarantee a valid transformation between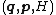 and
and 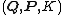 , we may resort to an indirect generating function approach. Both sets of variables must obey Hamilton's principle
, we may resort to an indirect generating function approach. Both sets of variables must obey Hamilton's principleAction (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...


To satisfy both variational integrals
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
, we must have
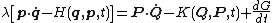
In general, the scaling factor
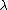 is set equal to one; canonical transformations for which
is set equal to one; canonical transformations for which  are called extended canonical transformations.
are called extended canonical transformations.Here
 is a generating function
is a generating functionGenerating function (physics)
Generating functions which arise in Hamiltonian mechanics are quite different from generating functions in mathematics. In the case of physics, generating functions act as a bridge between two sets of canonical variables when performing canonical transformation.-Details:There are four basic...
of one old canonical coordinate
Canonical coordinates
In mathematics and classical mechanics, canonical coordinates are particular sets of coordinates on the phase space, or equivalently, on the cotangent manifold of a manifold. Canonical coordinates arise naturally in physics in the study of Hamiltonian mechanics...
(
 or
or  ), one new canonical coordinate
), one new canonical coordinateCanonical coordinates
In mathematics and classical mechanics, canonical coordinates are particular sets of coordinates on the phase space, or equivalently, on the cotangent manifold of a manifold. Canonical coordinates arise naturally in physics in the study of Hamiltonian mechanics...
(
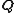 or
or 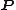 ) and (possibly) the time
) and (possibly) the time  . Thus, there are four basic types of generating functions, depending on the choice of variables.
. Thus, there are four basic types of generating functions, depending on the choice of variables.As will be shown below, the generating function will define a transformation from old to new canonical coordinates
Canonical coordinates
In mathematics and classical mechanics, canonical coordinates are particular sets of coordinates on the phase space, or equivalently, on the cotangent manifold of a manifold. Canonical coordinates arise naturally in physics in the study of Hamiltonian mechanics...
, and any such transformation
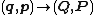 is guaranteed to be canonical.
is guaranteed to be canonical.Type 1 generating function
The type 1 generating function depends only on the old and new generalized coordinates
depends only on the old and new generalized coordinates
To derive the implicit transformation, we expand the defining equation above
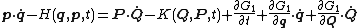
Since the new and old coordinates are each independent, the following
 equations must hold
equations must hold

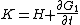
These equations define the transformation
 as follows. The first set of
as follows. The first set of  equations
equations
define relations between the new generalized coordinates
Generalized coordinates
In the study of multibody systems, generalized coordinates are a set of coordinates used to describe the configuration of a system relative to some reference configuration....
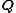 and the old canonical coordinates
and the old canonical coordinatesCanonical coordinates
In mathematics and classical mechanics, canonical coordinates are particular sets of coordinates on the phase space, or equivalently, on the cotangent manifold of a manifold. Canonical coordinates arise naturally in physics in the study of Hamiltonian mechanics...
 . Ideally, one can invert these relations to obtain formulae for each
. Ideally, one can invert these relations to obtain formulae for each 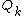 as a function of the old canonical coordinates. Substitution of these formulae for the
as a function of the old canonical coordinates. Substitution of these formulae for the 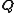 coordinates into the second set of
coordinates into the second set of 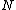 equations
equations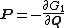
yields analogous formulae for the new generalized momenta
 in terms of the old canonical coordinates
in terms of the old canonical coordinatesCanonical coordinates
In mathematics and classical mechanics, canonical coordinates are particular sets of coordinates on the phase space, or equivalently, on the cotangent manifold of a manifold. Canonical coordinates arise naturally in physics in the study of Hamiltonian mechanics...
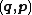 . We then invert both sets of formulae to obtain the old canonical coordinates
. We then invert both sets of formulae to obtain the old canonical coordinatesCanonical coordinates
In mathematics and classical mechanics, canonical coordinates are particular sets of coordinates on the phase space, or equivalently, on the cotangent manifold of a manifold. Canonical coordinates arise naturally in physics in the study of Hamiltonian mechanics...
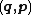 as functions of the new canonical coordinates
as functions of the new canonical coordinatesCanonical coordinates
In mathematics and classical mechanics, canonical coordinates are particular sets of coordinates on the phase space, or equivalently, on the cotangent manifold of a manifold. Canonical coordinates arise naturally in physics in the study of Hamiltonian mechanics...
 . Substitution of the inverted formulae into the final equation
. Substitution of the inverted formulae into the final equation
yields a formula for
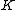 as a function of the new canonical coordinates
as a function of the new canonical coordinatesCanonical coordinates
In mathematics and classical mechanics, canonical coordinates are particular sets of coordinates on the phase space, or equivalently, on the cotangent manifold of a manifold. Canonical coordinates arise naturally in physics in the study of Hamiltonian mechanics...
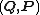 .
.In practice, this procedure is easier than it sounds, because the generating function is usually simple. For example, let

This results in swapping the generalized coordinates for the momenta and vice versa
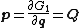

and
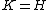 . This example illustrates how independent the coordinates and momenta are in the Hamiltonian formulation; they're equivalent variables.
. This example illustrates how independent the coordinates and momenta are in the Hamiltonian formulation; they're equivalent variables. Type 2 generating function
The type 2 generating function depends only on the old generalized coordinates
depends only on the old generalized coordinatesGeneralized coordinates
In the study of multibody systems, generalized coordinates are a set of coordinates used to describe the configuration of a system relative to some reference configuration....
and the new generalized momenta

where the
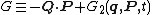 terms represent a Legendre transformation
terms represent a Legendre transformationLegendre transformation
In mathematics, the Legendre transformation or Legendre transform, named after Adrien-Marie Legendre, is an operation that transforms one real-valued function of a real variable into another...
to change the right-hand side of the equation below. To derive the implicit transformation, we expand the defining equation above

Since the old coordinates and new momenta are each independent, the following
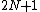 equations must hold
equations must hold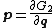
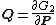

These equations define the transformation
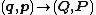 as follows. The first set of
as follows. The first set of  equations
equations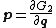
define relations between the new generalized momenta
 and the old canonical coordinates
and the old canonical coordinatesCanonical coordinates
In mathematics and classical mechanics, canonical coordinates are particular sets of coordinates on the phase space, or equivalently, on the cotangent manifold of a manifold. Canonical coordinates arise naturally in physics in the study of Hamiltonian mechanics...
 . Ideally, one can invert these relations to obtain formulae for each
. Ideally, one can invert these relations to obtain formulae for each 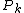 as a function of the old canonical coordinates. Substitution of these formulae for the
as a function of the old canonical coordinates. Substitution of these formulae for the 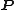 coordinates into the second set of
coordinates into the second set of 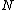 equations
equations
yields analogous formulae for the new generalized coordinates
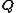 in terms of the old canonical coordinates
in terms of the old canonical coordinatesCanonical coordinates
In mathematics and classical mechanics, canonical coordinates are particular sets of coordinates on the phase space, or equivalently, on the cotangent manifold of a manifold. Canonical coordinates arise naturally in physics in the study of Hamiltonian mechanics...
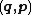 . We then invert both sets of formulae to obtain the old canonical coordinates
. We then invert both sets of formulae to obtain the old canonical coordinatesCanonical coordinates
In mathematics and classical mechanics, canonical coordinates are particular sets of coordinates on the phase space, or equivalently, on the cotangent manifold of a manifold. Canonical coordinates arise naturally in physics in the study of Hamiltonian mechanics...
 as functions of the new canonical coordinates
as functions of the new canonical coordinatesCanonical coordinates
In mathematics and classical mechanics, canonical coordinates are particular sets of coordinates on the phase space, or equivalently, on the cotangent manifold of a manifold. Canonical coordinates arise naturally in physics in the study of Hamiltonian mechanics...
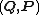 . Substitution of the inverted formulae into the final equation
. Substitution of the inverted formulae into the final equation
yields a formula for
 as a function of the new canonical coordinates
as a function of the new canonical coordinatesCanonical coordinates
In mathematics and classical mechanics, canonical coordinates are particular sets of coordinates on the phase space, or equivalently, on the cotangent manifold of a manifold. Canonical coordinates arise naturally in physics in the study of Hamiltonian mechanics...
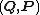 .
.In practice, this procedure is easier than it sounds, because the generating function is usually simple. For example, let
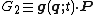
where
 is a set of
is a set of  functions.
functions.This results in a point transformation of the generalized coordinates

Type 3 generating function
The type 3 generating function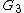 depends only on the old generalized momenta and the new generalized coordinates
depends only on the old generalized momenta and the new generalized coordinates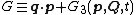
where the
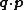 terms represent a Legendre transformation
terms represent a Legendre transformationLegendre transformation
In mathematics, the Legendre transformation or Legendre transform, named after Adrien-Marie Legendre, is an operation that transforms one real-valued function of a real variable into another...
to change the left-hand side of the equation below. To derive the implicit transformation, we expand the defining equation above
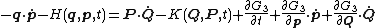
Since the new and old coordinates are each independent, the following
 equations must hold
equations must hold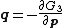

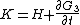
These equations define the transformation
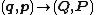 as follows. The first set of
as follows. The first set of 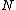 equations
equations
define relations between the new generalized coordinates
Generalized coordinates
In the study of multibody systems, generalized coordinates are a set of coordinates used to describe the configuration of a system relative to some reference configuration....
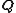 and the old canonical coordinates
and the old canonical coordinatesCanonical coordinates
In mathematics and classical mechanics, canonical coordinates are particular sets of coordinates on the phase space, or equivalently, on the cotangent manifold of a manifold. Canonical coordinates arise naturally in physics in the study of Hamiltonian mechanics...
 . Ideally, one can invert these relations to obtain formulae for each
. Ideally, one can invert these relations to obtain formulae for each 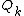 as a function of the old canonical coordinates. Substitution of these formulae for the
as a function of the old canonical coordinates. Substitution of these formulae for the  coordinates into the second set of
coordinates into the second set of 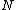 equations
equations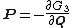
yields analogous formulae for the new generalized momenta
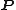 in terms of the old canonical coordinates
in terms of the old canonical coordinatesCanonical coordinates
In mathematics and classical mechanics, canonical coordinates are particular sets of coordinates on the phase space, or equivalently, on the cotangent manifold of a manifold. Canonical coordinates arise naturally in physics in the study of Hamiltonian mechanics...
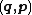 . We then invert both sets of formulae to obtain the old canonical coordinates
. We then invert both sets of formulae to obtain the old canonical coordinatesCanonical coordinates
In mathematics and classical mechanics, canonical coordinates are particular sets of coordinates on the phase space, or equivalently, on the cotangent manifold of a manifold. Canonical coordinates arise naturally in physics in the study of Hamiltonian mechanics...
 as functions of the new canonical coordinates
as functions of the new canonical coordinatesCanonical coordinates
In mathematics and classical mechanics, canonical coordinates are particular sets of coordinates on the phase space, or equivalently, on the cotangent manifold of a manifold. Canonical coordinates arise naturally in physics in the study of Hamiltonian mechanics...
 . Substitution of the inverted formulae into the final equation
. Substitution of the inverted formulae into the final equation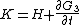
yields a formula for
 as a function of the new canonical coordinates
as a function of the new canonical coordinatesCanonical coordinates
In mathematics and classical mechanics, canonical coordinates are particular sets of coordinates on the phase space, or equivalently, on the cotangent manifold of a manifold. Canonical coordinates arise naturally in physics in the study of Hamiltonian mechanics...
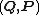 .
.In practice, this procedure is easier than it sounds, because the generating function is usually simple.
Type 4 generating function
The type 4 generating function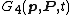 depends only on the old and new generalized momenta
depends only on the old and new generalized momenta
where the
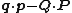 terms represent a Legendre transformation
terms represent a Legendre transformationLegendre transformation
In mathematics, the Legendre transformation or Legendre transform, named after Adrien-Marie Legendre, is an operation that transforms one real-valued function of a real variable into another...
to change both sides of the equation below. To derive the implicit transformation, we expand the defining equation above

Since the new and old coordinates are each independent, the following
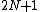 equations must hold
equations must hold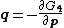
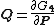
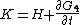
These equations define the transformation
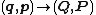 as follows. The first set of
as follows. The first set of 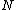 equations
equations
define relations between the new generalized momenta
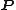 and the old canonical coordinates
and the old canonical coordinatesCanonical coordinates
In mathematics and classical mechanics, canonical coordinates are particular sets of coordinates on the phase space, or equivalently, on the cotangent manifold of a manifold. Canonical coordinates arise naturally in physics in the study of Hamiltonian mechanics...
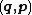 . Ideally, one can invert these relations to obtain formulae for each
. Ideally, one can invert these relations to obtain formulae for each 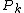 as a function of the old canonical coordinates. Substitution of these formulae for the
as a function of the old canonical coordinates. Substitution of these formulae for the 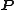 coordinates into the second set of
coordinates into the second set of 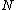 equations
equations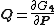
yields analogous formulae for the new generalized coordinates
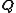 in terms of the old canonical coordinates
in terms of the old canonical coordinatesCanonical coordinates
In mathematics and classical mechanics, canonical coordinates are particular sets of coordinates on the phase space, or equivalently, on the cotangent manifold of a manifold. Canonical coordinates arise naturally in physics in the study of Hamiltonian mechanics...
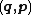 . We then invert both sets of formulae to obtain the old canonical coordinates
. We then invert both sets of formulae to obtain the old canonical coordinatesCanonical coordinates
In mathematics and classical mechanics, canonical coordinates are particular sets of coordinates on the phase space, or equivalently, on the cotangent manifold of a manifold. Canonical coordinates arise naturally in physics in the study of Hamiltonian mechanics...
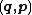 as functions of the new canonical coordinates
as functions of the new canonical coordinatesCanonical coordinates
In mathematics and classical mechanics, canonical coordinates are particular sets of coordinates on the phase space, or equivalently, on the cotangent manifold of a manifold. Canonical coordinates arise naturally in physics in the study of Hamiltonian mechanics...
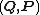 . Substitution of the inverted formulae into the final equation
. Substitution of the inverted formulae into the final equation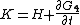
yields a formula for
 as a function of the new canonical coordinates
as a function of the new canonical coordinatesCanonical coordinates
In mathematics and classical mechanics, canonical coordinates are particular sets of coordinates on the phase space, or equivalently, on the cotangent manifold of a manifold. Canonical coordinates arise naturally in physics in the study of Hamiltonian mechanics...
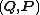 .
.Motion as a canonical transformation
Motion itself (or, equivalently, a shift in the time origin) is a canonical transformation. If and
and 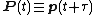 , then Hamilton's principle
, then Hamilton's principleAction (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
is automatically satisfied
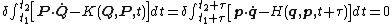
since a valid trajectory
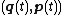 should always satisfy Hamilton's principle
should always satisfy Hamilton's principleAction (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
, regardless of the endpoints.
Modern mathematical description
In mathematical terms, canonical coordinatesCanonical coordinates
In mathematics and classical mechanics, canonical coordinates are particular sets of coordinates on the phase space, or equivalently, on the cotangent manifold of a manifold. Canonical coordinates arise naturally in physics in the study of Hamiltonian mechanics...
are any coordinates on the phase space (cotangent bundle
Cotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
) of the system that allow the canonical one-form to be written as
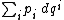
up to a total differential (exact form). The change of variable between one set of canonical coordinates and another is a canonical transformation. The index of the generalized coordinates
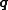 is written here as a superscript (
is written here as a superscript (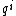 ), not as a subscript as done above (
), not as a subscript as done above (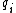 ). The superscript conveys the contravariant transformation properties
). The superscript conveys the contravariant transformation propertiesCovariance and contravariance
In multilinear algebra and tensor analysis, covariance and contravariance describe how the quantitative description of certain geometric or physical entities changes with a change of basis from one coordinate system to another. When one coordinate system is just a rotation of the other, this...
of the generalized coordinates, and does not mean that the coordinate is being raised to a power. Further details may be found at the symplectomorphism
Symplectomorphism
In mathematics, a symplectomorphism is an isomorphism in the category of symplectic manifolds.-Formal definition:A diffeomorphism between two symplectic manifolds f: \rightarrow is called symplectomorphism, iff^*\omega'=\omega,...
article.
History
The first major application of the canonical transformation was in 1846, by Charles DelaunayCharles-Eugène Delaunay
Charles-Eugène Delaunay was a French astronomer and mathematician. His lunar motion studies were important in advancing both the theory of planetary motion and mathematics.-Life:...
, in the study of the Earth-Moon-Sun system. This work resulted in the publication of a pair of large volumes as Mémoires by the French Academy of Sciences
French Academy of Sciences
The French Academy of Sciences is a learned society, founded in 1666 by Louis XIV at the suggestion of Jean-Baptiste Colbert, to encourage and protect the spirit of French scientific research...
, in 1860 and 1867.
See also
- SymplectomorphismSymplectomorphismIn mathematics, a symplectomorphism is an isomorphism in the category of symplectic manifolds.-Formal definition:A diffeomorphism between two symplectic manifolds f: \rightarrow is called symplectomorphism, iff^*\omega'=\omega,...
- Hamilton–Jacobi equationHamilton–Jacobi equationIn mathematics, the Hamilton–Jacobi equation is a necessary condition describing extremal geometry in generalizations of problems from the calculus of variations. In physics, the Hamilton–Jacobi equation is a reformulation of classical mechanics and, thus, equivalent to other formulations such as...
- Liouville's theorem (Hamiltonian)Liouville's theorem (Hamiltonian)In physics, Liouville's theorem, named after the French mathematician Joseph Liouville, is a key theorem in classical statistical and Hamiltonian mechanics...
- Mathieu transformationMathieu transformationThe Mathieu transformations make up a subgroup of canonical transformations preserving the differential form\sum_i p_i \delta q_i=\sum_i P_i \delta Q_i \,The transformation is named after the French mathematician Émile Léonard Mathieu.- Details :...
- Linear canonical transformationLinear canonical transformationIn Hamiltonian mechanics, the linear canonical transformation is a family of integral transforms that generalizes many classical transforms...

