Poisson algebra
Encyclopedia
In mathematics
, a Poisson algebra is an associative algebra
together with a Lie bracket
that also satisfies Leibniz' law
; that is, the bracket is also a derivation
. Poisson algebras appear naturally in Hamiltonian mechanics
, and are also central in the study of quantum group
s. Manifold
s with a Poisson algebra structure are known as Poisson manifold
s, of which the symplectic manifold
s and the Poisson-Lie group
s are a special case. The algebra is named in honour of Siméon-Denis Poisson.
over a field
K equipped with two bilinear
products,
and { , }, having the following properties:
The last property often allows a variety of different formulations of the algebra to be given, as noted in the examples below.
s over a symplectic manifold
forms a Poisson algebra. On a symplectic manifold, every real-valued function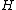
on the manifold induces a vector field 
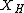, the Hamiltonian vector field
. Then, given any two smooth functions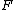
and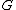 
over the symplectic manifold, the Poisson bracket {,} may be defined as:
.
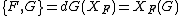This definition is consistent in part because the Poisson bracket acts as a derivation. Equivalently, one may define the bracket {,} as
where [,] is the Lie derivative
. When the symplectic manifold is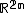
with the standard symplectic structure, then the Poisson bracket takes on the well-known form
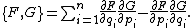
Similar considerations apply for Poisson manifold
s, which generalize symplectic manifolds by allowing the symplectic bivector to be vanishing on some (or trivially, all) of the manifold.
, then the commutator [x,y]≡xy−yx turns it into a Poisson algebra.
, the space 
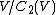is a Poisson algebra with 
and 
. For certain vertex operator algebras, these Poisson algebras are finite dimensional.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Poisson algebra is an associative algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
together with a Lie bracket
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
that also satisfies Leibniz' law
Product rule
In calculus, the product rule is a formula used to find the derivatives of products of two or more functions. It may be stated thus:'=f'\cdot g+f\cdot g' \,\! or in the Leibniz notation thus:...
; that is, the bracket is also a derivation
Derivation (abstract algebra)
In abstract algebra, a derivation is a function on an algebra which generalizes certain features of the derivative operator. Specifically, given an algebra A over a ring or a field K, a K-derivation is a K-linear map D: A → A that satisfies Leibniz's law: D = b + a.More...
. Poisson algebras appear naturally in Hamiltonian mechanics
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
, and are also central in the study of quantum group
Quantum group
In mathematics and theoretical physics, the term quantum group denotes various kinds of noncommutative algebra with additional structure. In general, a quantum group is some kind of Hopf algebra...
s. Manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s with a Poisson algebra structure are known as Poisson manifold
Poisson manifold
In mathematics, a Poisson manifold is a differentiable manifold M such that the algebra C^\infty\, of smooth functions over M is equipped with a bilinear map called the Poisson bracket, turning it into a Poisson algebra...
s, of which the symplectic manifold
Symplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
s and the Poisson-Lie group
Poisson-Lie group
In mathematics, a Poisson–Lie group is a Poisson manifold that is also a Lie group, with the group multiplication being compatible with the Poisson algebra structure on the manifold...
s are a special case. The algebra is named in honour of Siméon-Denis Poisson.
Definition
A Poisson algebra is a vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K equipped with two bilinear
Bilinear
Bilinear may refer to:* Bilinear sampling, a method in computer graphics for choosing the color of a texture* Bilinear form* Bilinear interpolation* Bilinear map, a type of mathematical function between vector spaces...
products,
and { , }, having the following properties:- The product
forms an associative K-algebraAssociative algebraIn mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
.
- The product { , }, called the Poisson bracketPoisson bracketIn mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time-evolution of a Hamiltonian dynamical system...
, forms a Lie algebraLie algebraIn mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
, and so it is anti-symmetric, and obeys the Jacobi identityJacobi identityIn mathematics the Jacobi identity is a property that a binary operation can satisfy which determines how the order of evaluation behaves for the given operation. Unlike for associative operations, order of evaluation is significant for operations satisfying Jacobi identity...
.
- The Poisson bracket acts as a derivationDerivation (abstract algebra)In abstract algebra, a derivation is a function on an algebra which generalizes certain features of the derivative operator. Specifically, given an algebra A over a ring or a field K, a K-derivation is a K-linear map D: A → A that satisfies Leibniz's law: D = b + a.More...
of the associative product
, so that for any three elements x, y and z in the algebra, one has {x, y
z} = {x, y}
z + y
{x, z}.
The last property often allows a variety of different formulations of the algebra to be given, as noted in the examples below.
Symplectic manifolds
The space of real-valued smooth functionSmooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
s over a symplectic manifold
Symplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
forms a Poisson algebra. On a symplectic manifold, every real-valued function
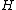on the manifold induces a vector field 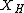, the Hamiltonian vector fieldHamiltonian vector field
In mathematics and physics, a Hamiltonian vector field on a symplectic manifold is a vector field, defined for any energy function or Hamiltonian. Named after the physicist and mathematician Sir William Rowan Hamilton, a Hamiltonian vector field is a geometric manifestation of Hamilton's equations...
. Then, given any two smooth functions
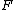and 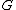over the symplectic manifold, the Poisson bracket {,} may be defined as: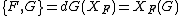.This definition is consistent in part because the Poisson bracket acts as a derivation. Equivalently, one may define the bracket {,} as
where [,] is the Lie derivative
Lie derivative
In mathematics, the Lie derivative , named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a vector field or more generally a tensor field, along the flow of another vector field...
. When the symplectic manifold is
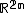with the standard symplectic structure, then the Poisson bracket takes on the well-known form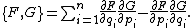Similar considerations apply for Poisson manifold
Poisson manifold
In mathematics, a Poisson manifold is a differentiable manifold M such that the algebra C^\infty\, of smooth functions over M is equipped with a bilinear map called the Poisson bracket, turning it into a Poisson algebra...
s, which generalize symplectic manifolds by allowing the symplectic bivector to be vanishing on some (or trivially, all) of the manifold.
Associative algebras
If A is a associative algebraAssociative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
, then the commutator [x,y]≡xy−yx turns it into a Poisson algebra.
Vertex operator algebras
For a vertex operator algebraVertex operator algebra
In mathematics, a vertex operator algebra is an algebraic structure that plays an important role in conformal field theory and related areas of physics...
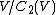, the space is a Poisson algebra with and . For certain vertex operator algebras, these Poisson algebras are finite dimensional.