
Conserved quantity
Encyclopedia
In mathematics, a conserved quantity of a dynamical system
is a function H of the dependent variables that is a constant (in other words, conserved) along each trajectory of the system. A conserved quantity can be a useful tool for qualitative analysis. Not all systems have conserved quantities, however the existence has nothing to do with linearity (a simplifying trait in a system) which means that finding and examining conserved quantities can be useful in understanding nonlinear systems.
Conserved quantities are not unique, since one can always add a constant to a conserved quantity.
Since most laws of physics express some kind of conservation, conserved quantities commonly exist in mathematic models of real systems. For example, any classical mechanics
model will have energy
as a conserved quantity so long as the forces involved are conservative
.
s
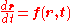
where bold indicates vector quantities, a scalar-valued function H(r) is a conserved quantity of the system if, for all time and initial conditions in some specific domain,
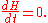
Note that by using the multivariate chain rule,
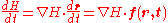
so that the definition may be written as
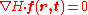
which contains information specific to the system and can be helpful in finding conserved quantities, or establishing whether or not a conserved quantity exists.
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
is a function H of the dependent variables that is a constant (in other words, conserved) along each trajectory of the system. A conserved quantity can be a useful tool for qualitative analysis. Not all systems have conserved quantities, however the existence has nothing to do with linearity (a simplifying trait in a system) which means that finding and examining conserved quantities can be useful in understanding nonlinear systems.
Conserved quantities are not unique, since one can always add a constant to a conserved quantity.
Since most laws of physics express some kind of conservation, conserved quantities commonly exist in mathematic models of real systems. For example, any classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
model will have energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
as a conserved quantity so long as the forces involved are conservative
Conservative force
A conservative force is a force with the property that the work done in moving a particle between two points is independent of the path taken. Equivalently, if a particle travels in a closed loop, the net work done by a conservative force is zero.It is possible to define a numerical value of...
.
Differential equations
For a first order system of differential equationDifferential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s
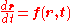
where bold indicates vector quantities, a scalar-valued function H(r) is a conserved quantity of the system if, for all time and initial conditions in some specific domain,
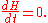
Note that by using the multivariate chain rule,
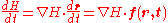
so that the definition may be written as
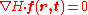
which contains information specific to the system and can be helpful in finding conserved quantities, or establishing whether or not a conserved quantity exists.

