Sub-Riemannian manifold
Encyclopedia
In mathematics
, a sub-Riemannian manifold is a certain type of generalization of a Riemannian manifold
. Roughly speaking, to measure distances in a sub-Riemannian manifold, you are allowed to go only along curves tangent to so-called horizontal subspaces.
Sub-Riemannian manifolds (and so, a fortiori, Riemannian manifolds) carry a natural intrinsic metric
called the metric of Carnot–Carathéodory. The Hausdorff dimension
of such metric space
s is always an integer
and larger than its topological dimension (unless it is actually a Riemannian manifold).
Sub-Riemannian manifolds often occur in the study of constrained systems in classical mechanics
, such as the motion of vehicles on a surface, the motion of robot arms, and the orbital dynamics of satellites. Geometric quantities such as the Berry phase may be understood in the language of sub-Riemannian geometry. The Heisenberg group, important to quantum mechanics
, carries a natural sub-Riemannian structure.
we mean a subbundle
of the tangent bundle
of
.
Given a distribution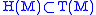
a vector field in 
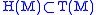is called horizontal. A curve 
on 
is called horizontal if 
for any
.
A distribution on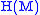
is called completely non-integrable if for any 
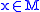we have that any tangent vector can be presented as a linear combination
of vectors of the following types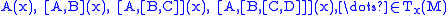
where all vector fields 
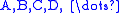are horizontal.
A sub-Riemannian manifold is a triple
, where 
is a differentiable manifold
,
is a completely non-integrable "horizontal" distribution and 
is a smooth section of positive-definite quadratic form
s on
.
Any sub-Riemannian manifold carries the natural intrinsic metric
, called the metric of Carnot–Carathéodory, defined as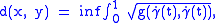
where infimum is taken along all horizontal curves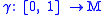
such that 
, 
.
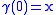and 
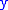for the location and an angle 
which describes the orientation of the car. Therefore, the position of car can be described by a point in a manifold
One can ask, what is the minimal distance one should drive to get from one position to another? This defines a Carnot–Carathéodory metric on the manifold
A closely related example of a sub-Riemannian metric can be constructed on a Heisenberg group: Take two elements
and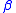 
in the corresponding Lie algebra such that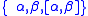
spans the entire algebra. The horizontal distribution
spanned by left shifts of 
and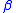 
is completely non-integrable. Then choosing any smooth positive quadratic form on 
gives a sub-Riemannian metric on the group.
, called the sub-Riemannian Hamiltonian, constructed out of the metric for the manifold. Conversely, every such quadratic Hamiltonian induces a sub-Riemannian manifold. The existence of geodesics of the corresponding Hamilton–Jacobi equation
s for the sub-Riemannian Hamiltonian are given by the Chow–Rashevskii theorem.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a sub-Riemannian manifold is a certain type of generalization of a Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
. Roughly speaking, to measure distances in a sub-Riemannian manifold, you are allowed to go only along curves tangent to so-called horizontal subspaces.
Sub-Riemannian manifolds (and so, a fortiori, Riemannian manifolds) carry a natural intrinsic metric
Intrinsic metric
In the mathematical study of metric spaces, one can consider the arclength of paths in the space. If two points are a given distance from each other, it is natural to expect that one should be able to get from one point to another along a path whose arclength is equal to that distance...
called the metric of Carnot–Carathéodory. The Hausdorff dimension
Hausdorff dimension
thumb|450px|Estimating the Hausdorff dimension of the coast of Great BritainIn mathematics, the Hausdorff dimension is an extended non-negative real number associated with any metric space. The Hausdorff dimension generalizes the notion of the dimension of a real vector space...
of such metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s is always an integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
and larger than its topological dimension (unless it is actually a Riemannian manifold).
Sub-Riemannian manifolds often occur in the study of constrained systems in classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
, such as the motion of vehicles on a surface, the motion of robot arms, and the orbital dynamics of satellites. Geometric quantities such as the Berry phase may be understood in the language of sub-Riemannian geometry. The Heisenberg group, important to quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, carries a natural sub-Riemannian structure.
Definitions
By a distribution on we mean a subbundleSubbundle
In mathematics, a subbundle U of a vector bundle V on a topological space X is a collection of linear subspaces Ux of the fibers Vx of V at x in X, that make up a vector bundle in their own right....
of the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
of
.Given a distribution
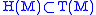a vector field in 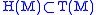is called horizontal. A curve on is called horizontal if for any.A distribution on
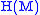is called completely non-integrable if for any 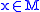we have that any tangent vector can be presented as a linear combinationLinear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of vectors of the following types
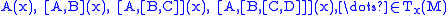where all vector fields 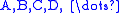are horizontal.A sub-Riemannian manifold is a triple
, where is a differentiable manifoldManifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
,
is a completely non-integrable "horizontal" distribution and is a smooth section of positive-definite quadratic formQuadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
s on
.Any sub-Riemannian manifold carries the natural intrinsic metric
Intrinsic metric
In the mathematical study of metric spaces, one can consider the arclength of paths in the space. If two points are a given distance from each other, it is natural to expect that one should be able to get from one point to another along a path whose arclength is equal to that distance...
, called the metric of Carnot–Carathéodory, defined as
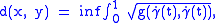
where infimum is taken along all horizontal curves
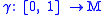such that 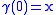, .Examples
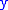A position of a car on the plane is determined by three parameters: two coordinates and for the location and an angle which describes the orientation of the car. Therefore, the position of car can be described by a point in a manifoldOne can ask, what is the minimal distance one should drive to get from one position to another? This defines a Carnot–Carathéodory metric on the manifold
A closely related example of a sub-Riemannian metric can be constructed on a Heisenberg group: Take two elements
and 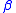in the corresponding Lie algebra such that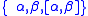spans the entire algebra. The horizontal distribution
spanned by left shifts of and 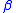is completely non-integrable. Then choosing any smooth positive quadratic form on gives a sub-Riemannian metric on the group.Properties
For every sub-Riemannian manifold, there exists a HamiltonianHamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
, called the sub-Riemannian Hamiltonian, constructed out of the metric for the manifold. Conversely, every such quadratic Hamiltonian induces a sub-Riemannian manifold. The existence of geodesics of the corresponding Hamilton–Jacobi equation
Hamilton–Jacobi equation
In mathematics, the Hamilton–Jacobi equation is a necessary condition describing extremal geometry in generalizations of problems from the calculus of variations. In physics, the Hamilton–Jacobi equation is a reformulation of classical mechanics and, thus, equivalent to other formulations such as...
s for the sub-Riemannian Hamiltonian are given by the Chow–Rashevskii theorem.