Fréchet derivative
Encyclopedia
In mathematics
, the Fréchet derivative is a derivative
defined on Banach space
s. Named after Maurice Fréchet, it is commonly used to formalize the concept of the functional derivative
used widely in the calculus of variations
. Intuitively, it generalizes the idea of linear approximation
from function
s of one variable to functions on Banach spaces. The Fréchet derivative should be contrasted to the more general Gâteaux derivative
which is a generalization of the classical directional derivative
.
The Fréchet derivative has applications throughout mathematical analysis
, and in particular to the calculus of variations and much of nonlinear analysis and nonlinear functional analysis
. It has applications to nonlinear problems throughout the sciences.
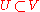be an open subset of V. A function f : U → W is called Fréchet differentiable at 
if there exists a bounded linear operator 
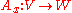such that
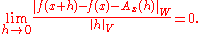
The limit
here is meant in the usual sense of a limit of a function
defined on a metric space (see Functions on metric spaces), using V and W as the two metric spaces, and the above expression as the function of argument h in V. As a consequence, it must exist for all sequence
s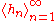
of non-zero elements of V which converge to the zero vector 
If the limit exists, we write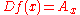 
and call it the (Fréchet) derivative of f at x. A function f that is Fréchet differentiable for any point of U, and whose derivative Df(x) is continuous in x on U, is said to be C1.
This notion of derivative is a generalization of the ordinary derivative of a function on the real number
s f : R → R since the linear maps from R to R are just multiplication by a real number. In this case, Df(x) is the function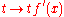
.
Differentiation is a linear operation in the following sense: if f and g are two maps V → W which are differentiable at x, and r and s are scalars (two real or complex number
s), then rf + sg is differentiable at x with D(rf + sg)(x) = rDf(x) + sDg(x).
The chain rule
is also valid in this context: if f : U → Y is differentiable at x in U, and g : Y → W is differentiable at y = f(x), then the composition g o f is differentiable in x and the derivative is the composition of the derivatives:
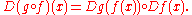
In particular, it is represented in coordinates by the Jacobian matrix.
Suppose that f is a map, f:U⊂Rn → Rm with U an open set. If f is Fréchet differentiable at a point a ∈ U, then its derivative is
where Jf(a) denotes the Jacobian matrix of f at a.
Furthermore, the partial derivatives of f are given by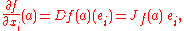
where {ei} is the canonical basis of Rn. Since the derivative is a linear function, we have for all vectors h ∈ Rn that the directional derivative
of f along h is given by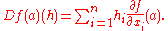
If all partial derivatives of f exist and are continuous, then f is Fréchet differentiable (and, in fact, C1). The converse is not true: a function may be Fréchet differentiable and yet fail to have continuous partial derivatives.
at x ∈ U if f has a directional derivative along all directions at x. This means that there exists a function such that
for any chosen vector h in V, and where t is from the scalar field associated with V (usually, t is real). If f is Fréchet differentiable at x, it is also Gâteaux differentiable there, and g is just the linear operator A = Df(x). However, not every Gâteaux differentiable function is Fréchet differentiable. If f is Gâteaux differentiable on an open set U ⊂ V, then f is Fréchet differentiable if its Gâteaux derivative is linear and bounded at each point of U and the Gâteaux derivative is a continuous map .
For example, the real-valued function f of two real variables defined by
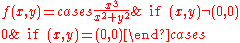
is continuous and Gâteaux differentiable at (0, 0), with its derivative being
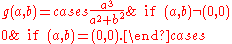
The function g is not a linear operator, so this function is not Fréchet differentiable.
More generally, any function of the form
, where r and φ are the polar coordinates of (x,y), is continuous and Gâteaux differentiable at (0,0) if g is differentiable at 0 and 
, but the Gâteaux derivative is only linear and the Fréchet derivative only exists if h is sinusoidal.
In another situation, the function f given by
is Gâteaux differentiable at (0, 0), with its derivative there being g(a, b) = 0 for all (a, b), which is a linear operator. However, f is not continuous at (0, 0) (one can see by approaching the origin along the curve (t, t3)) and therefore f cannot be Fréchet differentiable at the origin.
A more subtle example is
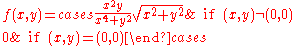
which is a continuous function that is Gâteaux differentiable at (0, 0), with its derivative being g(a, b) = 0 there, which is again linear. However, f is not Fréchet differentiable. If it were, its Fréchet derivative would conincide with its Gâteaux derivative, and hence would be the zero operator; hence the limit
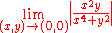
would have to be zero, whereas approaching the origin along the curve (t, t2) shows that this limit does not exist.
These cases can occur because the definition of the Gâteaux derivative only requires that the difference quotient
s converge along each direction individually, without making requirements about the rates of convergence for different directions. Thus, for a given ε, although for each direction the difference quotient is within ε of its limit in some neighborhood of the given point, these neighborhoods may be different for different directions, and there may be a sequence of directions for which these neighborhoods become arbitrarily small. If a sequence of points is chosen along these directions, the quotient in the definition of the Fréchet derivative, which considers all directions at once, may not converge. Thus, in order for a linear Gâteaux derivative to imply the existence of the Fréchet derivative, the difference quotients have to converge uniformly for all directions.
The following example only works in infinite dimensions. Let X be a Banach space, and φ a linear functional
on X that is discontinuous at x = 0 (a discontinuous linear functional). Let
Then f(x) is Gâteaux differentiable at x = 0 with derivative 0. However, f(x) is not Fréchet differentiable since the limit
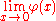
does not exist.
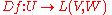
is a function from U to the space L(V, W) of all bounded linear operators from V to W. This function may also have a derivative, the second order derivative of f, which, by the definition of derivative, will be a map
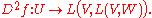
To make it easier to work with second-order derivatives, the space on the right-hand side is identified with the Banach space L2(V×V, W) of all continuous bilinear maps from V to W. An element φ in L(V, L(V, W)) is thus identified with ψ in L2(V×V, W) such that for all x and y in V
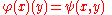
(intuitively: a function φ linear in x with φ(x) linear in y is the same as a bilinear function ψ in x and y).
One may differentiate
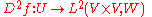
again, to obtain the third order derivative, which at each point will be a trilinear map, and so on. The n-th derivative will be a function
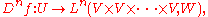
taking values in the Banach space of continuous multilinear maps in n arguments from V to W. Recursively, a function f is n+1 times differentiable on U if it is n times differentiable on U and for each x in U there exists a continuous multilinear map A of n+1 arguments such that the limit
exists uniformly for h1, h2, ..., hn in bounded sets in V. In that case, A is the n+1st derivative of f at x.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Fréchet derivative is a derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
defined on Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s. Named after Maurice Fréchet, it is commonly used to formalize the concept of the functional derivative
Functional derivative
In mathematics and theoretical physics, the functional derivative is a generalization of the gradient. While the latter differentiates with respect to a vector with discrete components, the former differentiates with respect to a continuous function. Both of these can be viewed as extensions of...
used widely in the calculus of variations
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
. Intuitively, it generalizes the idea of linear approximation
Linear approximation
In mathematics, a linear approximation is an approximation of a general function using a linear function . They are widely used in the method of finite differences to produce first order methods for solving or approximating solutions to equations.-Definition:Given a twice continuously...
from function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s of one variable to functions on Banach spaces. The Fréchet derivative should be contrasted to the more general Gâteaux derivative
Gâteaux derivative
In mathematics, the Gâteaux differential or Gâteaux derivative is a generalization of the concept of directional derivative in differential calculus. Named after René Gâteaux, a French mathematician who died young in World War I, it is defined for functions between locally convex topological vector...
which is a generalization of the classical directional derivative
Directional derivative
In mathematics, the directional derivative of a multivariate differentiable function along a given vector V at a given point P intuitively represents the instantaneous rate of change of the function, moving through P in the direction of V...
.
The Fréchet derivative has applications throughout mathematical analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, and in particular to the calculus of variations and much of nonlinear analysis and nonlinear functional analysis
Nonlinear functional analysis
Nonlinear functional analysis is a branch of Mathematical Analysis. It deals with nonlinear mappings and its subject matter includes:* generalizations of calculus to Banach spaces* implicit function theorems...
. It has applications to nonlinear problems throughout the sciences.
Definition
Let V and W be Banach spaces, and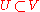 be an open subset of V. A function f : U → W is called Fréchet differentiable at if there exists a bounded linear operator 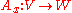such that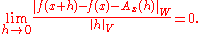The limit
Limit (mathematics)
In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...
here is meant in the usual sense of a limit of a function
Limit of a function
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
defined on a metric space (see Functions on metric spaces), using V and W as the two metric spaces, and the above expression as the function of argument h in V. As a consequence, it must exist for all sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
s
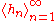of non-zero elements of V which converge to the zero vector If the limit exists, we write 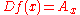and call it the (Fréchet) derivative of f at x. A function f that is Fréchet differentiable for any point of U, and whose derivative Df(x) is continuous in x on U, is said to be C1.This notion of derivative is a generalization of the ordinary derivative of a function on the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s f : R → R since the linear maps from R to R are just multiplication by a real number. In this case, Df(x) is the function
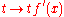.Properties
A function differentiable at a point is continuous at that point.Differentiation is a linear operation in the following sense: if f and g are two maps V → W which are differentiable at x, and r and s are scalars (two real or complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s), then rf + sg is differentiable at x with D(rf + sg)(x) = rDf(x) + sDg(x).
The chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
is also valid in this context: if f : U → Y is differentiable at x in U, and g : Y → W is differentiable at y = f(x), then the composition g o f is differentiable in x and the derivative is the composition of the derivatives:
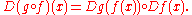
Finite dimensions
The Fréchet derivative in finite-dimensional spaces is the usual derivative.In particular, it is represented in coordinates by the Jacobian matrix.
Suppose that f is a map, f:U⊂Rn → Rm with U an open set. If f is Fréchet differentiable at a point a ∈ U, then its derivative is
where Jf(a) denotes the Jacobian matrix of f at a.
Furthermore, the partial derivatives of f are given by
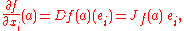
where {ei} is the canonical basis of Rn. Since the derivative is a linear function, we have for all vectors h ∈ Rn that the directional derivative
Directional derivative
In mathematics, the directional derivative of a multivariate differentiable function along a given vector V at a given point P intuitively represents the instantaneous rate of change of the function, moving through P in the direction of V...
of f along h is given by
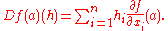
If all partial derivatives of f exist and are continuous, then f is Fréchet differentiable (and, in fact, C1). The converse is not true: a function may be Fréchet differentiable and yet fail to have continuous partial derivatives.
Relation to the Gâteaux derivative
A function f : U ⊂ V → W is called Gâteaux differentiableGâteaux derivative
In mathematics, the Gâteaux differential or Gâteaux derivative is a generalization of the concept of directional derivative in differential calculus. Named after René Gâteaux, a French mathematician who died young in World War I, it is defined for functions between locally convex topological vector...
at x ∈ U if f has a directional derivative along all directions at x. This means that there exists a function such that
for any chosen vector h in V, and where t is from the scalar field associated with V (usually, t is real). If f is Fréchet differentiable at x, it is also Gâteaux differentiable there, and g is just the linear operator A = Df(x). However, not every Gâteaux differentiable function is Fréchet differentiable. If f is Gâteaux differentiable on an open set U ⊂ V, then f is Fréchet differentiable if its Gâteaux derivative is linear and bounded at each point of U and the Gâteaux derivative is a continuous map .
For example, the real-valued function f of two real variables defined by
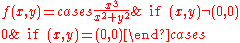
is continuous and Gâteaux differentiable at (0, 0), with its derivative being
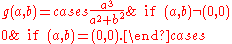
The function g is not a linear operator, so this function is not Fréchet differentiable.
More generally, any function of the form
, where r and φ are the polar coordinates of (x,y), is continuous and Gâteaux differentiable at (0,0) if g is differentiable at 0 and , but the Gâteaux derivative is only linear and the Fréchet derivative only exists if h is sinusoidal.In another situation, the function f given by
is Gâteaux differentiable at (0, 0), with its derivative there being g(a, b) = 0 for all (a, b), which is a linear operator. However, f is not continuous at (0, 0) (one can see by approaching the origin along the curve (t, t3)) and therefore f cannot be Fréchet differentiable at the origin.
A more subtle example is
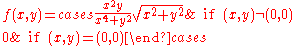
which is a continuous function that is Gâteaux differentiable at (0, 0), with its derivative being g(a, b) = 0 there, which is again linear. However, f is not Fréchet differentiable. If it were, its Fréchet derivative would conincide with its Gâteaux derivative, and hence would be the zero operator; hence the limit
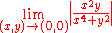
would have to be zero, whereas approaching the origin along the curve (t, t2) shows that this limit does not exist.
These cases can occur because the definition of the Gâteaux derivative only requires that the difference quotient
Difference quotient
The primary vehicle of calculus and other higher mathematics is the function. Its "input value" is its argument, usually a point expressible on a graph...
s converge along each direction individually, without making requirements about the rates of convergence for different directions. Thus, for a given ε, although for each direction the difference quotient is within ε of its limit in some neighborhood of the given point, these neighborhoods may be different for different directions, and there may be a sequence of directions for which these neighborhoods become arbitrarily small. If a sequence of points is chosen along these directions, the quotient in the definition of the Fréchet derivative, which considers all directions at once, may not converge. Thus, in order for a linear Gâteaux derivative to imply the existence of the Fréchet derivative, the difference quotients have to converge uniformly for all directions.
The following example only works in infinite dimensions. Let X be a Banach space, and φ a linear functional
Linear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
on X that is discontinuous at x = 0 (a discontinuous linear functional). Let
Then f(x) is Gâteaux differentiable at x = 0 with derivative 0. However, f(x) is not Fréchet differentiable since the limit
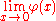
does not exist.
Higher derivatives
If f is a differentiable function at all points in an open subset U of V, it follows that its derivative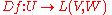is a function from U to the space L(V, W) of all bounded linear operators from V to W. This function may also have a derivative, the second order derivative of f, which, by the definition of derivative, will be a map
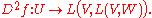
To make it easier to work with second-order derivatives, the space on the right-hand side is identified with the Banach space L2(V×V, W) of all continuous bilinear maps from V to W. An element φ in L(V, L(V, W)) is thus identified with ψ in L2(V×V, W) such that for all x and y in V
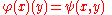
(intuitively: a function φ linear in x with φ(x) linear in y is the same as a bilinear function ψ in x and y).
One may differentiate
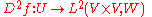
again, to obtain the third order derivative, which at each point will be a trilinear map, and so on. The n-th derivative will be a function
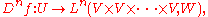
taking values in the Banach space of continuous multilinear maps in n arguments from V to W. Recursively, a function f is n+1 times differentiable on U if it is n times differentiable on U and for each x in U there exists a continuous multilinear map A of n+1 arguments such that the limit
exists uniformly for h1, h2, ..., hn in bounded sets in V. In that case, A is the n+1st derivative of f at x.
External links
- B. A. Frigyik, S. Srivastava and M. R. Gupta, Introduction to Functional Derivatives, UWEE Tech Report 2008-0001.
- http://www.probability.net. This webpage is mostly about basic probability and measure theory, but there is nice chapter about Frechet derivative in Banach spaces (chapter about Jacobian formula). All the results are given with proof.