
List of Banach spaces
Encyclopedia
In the mathematical
field of functional analysis
, Banach space
s are among the most important objects of study. In other areas of mathematical analysis
, most spaces which arise in practice turn out to be Banach spaces as well.
Here K denotes the field
of real numbers or complex numbers and I is a closed and bounded interval [a,b]. The number p is a real number
with , and q is its Hölder conjugate (also with ), so that the next equation holds:
and thus
The symbol Σ denotes a σ-algebra of sets, and Ξ denotes just an algebra of sets (for spaces only requiring finite additivity, such as the ba space
). The symbol μ denotes a positive measure: that is, a real-valued positive set function defined on a σ-algebra which is countably additive.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s are among the most important objects of study. In other areas of mathematical analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, most spaces which arise in practice turn out to be Banach spaces as well.
Classical Banach spaces
According to , the classical Banach spaces are those defined by , which is the source for the following table.Here K denotes the field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
of real numbers or complex numbers and I is a closed and bounded interval [a,b]. The number p is a real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
with , and q is its Hölder conjugate (also with ), so that the next equation holds:
and thus
The symbol Σ denotes a σ-algebra of sets, and Ξ denotes just an algebra of sets (for spaces only requiring finite additivity, such as the ba space
Ba space
In mathematics, the ba space ba of an algebra of sets \Sigma is the Banach space consisting of all bounded and finitely additive measures on \Sigma. The norm is defined as the variation, that is \|\nu\|=|\nu|....
). The symbol μ denotes a positive measure: that is, a real-valued positive set function defined on a σ-algebra which is countably additive.
| Classical Banach spaces | |||||
| Dual space Dual space In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra... | Reflexive Reflexive space In functional analysis, a Banach space is called reflexive if it coincides with the dual of its dual space in the topological and algebraic senses. Reflexive Banach spaces are often characterized by their geometric properties.- Normed spaces :Suppose X is a normed vector space over R or C... | weakly Weak topology In mathematics, weak topology is an alternative term for initial topology. The term is most commonly used for the initial topology of a topological vector space with respect to its continuous dual... complete | Norm | Notes | |
|---|---|---|---|---|---|
| Kn Euclidean space In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions... |
Kn | ||||
| ℓnp Lp space In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces... |
ℓnq | ||||
| ℓn∞ Lp space In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces... |
ℓn1 | ||||
| ℓp Lp space In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces... |
ℓq | ||||
| ℓ1 Lp space In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces... |
ℓ∞ | ||||
| ℓ∞ Lp space In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces... |
ba Ba space In mathematics, the ba space ba of an algebra of sets \Sigma is the Banach space consisting of all bounded and finitely additive measures on \Sigma. The norm is defined as the variation, that is \|\nu\|=|\nu|.... |
||||
| c C space In the mathematical field of functional analysis, the space denoted by c is the vector space of all convergent sequences of real numbers or complex numbers. When equipped with the uniform norm:\|x\|_\infty = \sup_n |x_n|... |
ℓ1 | ||||
| c0 | ℓ1 | Isomorphic but not isometric to c. | |||
| bv | ℓ1 + K | ||||
| bv0 | ℓ1 | ||||
| bs | ba Ba space In mathematics, the ba space ba of an algebra of sets \Sigma is the Banach space consisting of all bounded and finitely additive measures on \Sigma. The norm is defined as the variation, that is \|\nu\|=|\nu|.... |
Isometrically isomorphic to ℓ∞. | |||
| cs | ℓ1 | Isometrically isomorphic to c C space In the mathematical field of functional analysis, the space denoted by c is the vector space of all convergent sequences of real numbers or complex numbers. When equipped with the uniform norm:\|x\|_\infty = \sup_n |x_n|... . |
|||
| B(X, Ξ) Ba space In mathematics, the ba space ba of an algebra of sets \Sigma is the Banach space consisting of all bounded and finitely additive measures on \Sigma. The norm is defined as the variation, that is \|\nu\|=|\nu|.... |
ba(Ξ) Ba space In mathematics, the ba space ba of an algebra of sets \Sigma is the Banach space consisting of all bounded and finitely additive measures on \Sigma. The norm is defined as the variation, that is \|\nu\|=|\nu|.... |
||||
| C(X) Continuous functions on a compact Hausdorff space In mathematical analysis, and especially functional analysis, a fundamental role is played by the space of continuous functions on a compact Hausdorff space with values in the real or complex numbers. This space, denoted by C, is a vector space with respect to the pointwise addition of functions... |
rca(X) Ba space In mathematics, the ba space ba of an algebra of sets \Sigma is the Banach space consisting of all bounded and finitely additive measures on \Sigma. The norm is defined as the variation, that is \|\nu\|=|\nu|.... |
X is a compact Hausdorff space. | |||
| ba(Ξ) Ba space In mathematics, the ba space ba of an algebra of sets \Sigma is the Banach space consisting of all bounded and finitely additive measures on \Sigma. The norm is defined as the variation, that is \|\nu\|=|\nu|.... |
? | (variation of a measure) |
|||
| ca(Σ) Ba space In mathematics, the ba space ba of an algebra of sets \Sigma is the Banach space consisting of all bounded and finitely additive measures on \Sigma. The norm is defined as the variation, that is \|\nu\|=|\nu|.... |
? | ||||
| rca(Σ) Ba space In mathematics, the ba space ba of an algebra of sets \Sigma is the Banach space consisting of all bounded and finitely additive measures on \Sigma. The norm is defined as the variation, that is \|\nu\|=|\nu|.... |
? | ||||
| Lp(μ) Lp space In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces... |
Lq(μ) | ||||
| BV(I) Bounded variation In mathematical analysis, a function of bounded variation, also known as a BV function, is a real-valued function whose total variation is bounded : the graph of a function having this property is well behaved in a precise sense... |
? | Vf(I) is the total variation Total variation In mathematics, the total variation identifies several slightly different concepts, related to the structure of the codomain of a function or a measure... of f. |
|||
| NBV(I) Bounded variation In mathematical analysis, a function of bounded variation, also known as a BV function, is a real-valued function whose total variation is bounded : the graph of a function having this property is well behaved in a precise sense... |
? | NBV(I) consists of BV functions such that  . . |
|||
| AC(I) | K+L∞(I) | Isomorphic to the Sobolev space Sobolev space In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space... W1,1(I). |
|||
| Cn[a,b] | rca([a,b]) Ba space In mathematics, the ba space ba of an algebra of sets \Sigma is the Banach space consisting of all bounded and finitely additive measures on \Sigma. The norm is defined as the variation, that is \|\nu\|=|\nu|.... |
Isomorphic to Rn ⊕ C([a,b]), essentially by Taylor's theorem Taylor's theorem In calculus, Taylor's theorem gives an approximation of a k times differentiable function around a given point by a k-th order Taylor-polynomial. For analytic functions the Taylor polynomials at a given point are finite order truncations of its Taylor's series, which completely determines the... . |
|||
Banach spaces in other areas of analysis
- The Hardy spaceHardy spaceIn complex analysis, the Hardy spaces Hp are certain spaces of holomorphic functions on the unit disk or upper half plane. They were introduced by Frigyes Riesz , who named them after G. H. Hardy, because of the paper...
s - The space BMO of functions of bounded mean oscillationBounded mean oscillationIn harmonic analysis, a function of bounded mean oscillation, also known as a BMO function, is a real-valued function whose mean oscillation is bounded...
- The space of functions of bounded variationBounded variationIn mathematical analysis, a function of bounded variation, also known as a BV function, is a real-valued function whose total variation is bounded : the graph of a function having this property is well behaved in a precise sense...
- Sobolev spaceSobolev spaceIn mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
s - The Birnbaum–Orlicz spaceBirnbaum–Orlicz spaceIn the mathematical analysis, and especially in real and harmonic analysis, a Birnbaum–Orlicz space is a type of function space which generalizes the Lp spaces. Like the Lp spaces, they are Banach spaces...
s LA(μ). - Hölder spaces Ck,α(Ω).
- Lorentz spaceLorentz spaceIn mathematical analysis, Lorentz spaces, introduced by George Lorentz in the 1950s, are generalisations of the more familiar Lp spaces.The Lorentz spaces are denoted by Lp,q. Like the Lp spaces, they are characterized by a norm that encodes information about the "size" of a function, just as the...
Banach spaces serving as counterexamples
- Tsirelson spaceTsirelson spaceIn mathematics, Tsirelson space T is an example of a reflexive Banach space in which neither an l p space nor a c0 space can be embedded.It was introduced by B. S. Tsirelson in 1974...
- W.T. Gowers construction of a space X that is isomorphic to
 but not
but not 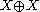 serves as a counterexample for weakening the premises of the Schroeder-Bernstein theorem
serves as a counterexample for weakening the premises of the Schroeder-Bernstein theorem



