Baire category theorem
Encyclopedia
The Baire category theorem is an important tool in general topology
and functional analysis
. The theorem has two forms, each of which gives sufficient conditions for a topological space
to be a Baire space
.
The theorem was proved by René-Louis Baire
in his 1899 doctoral thesis.
is a topological space with the following property: for each countable collection of open
dense set
s Un, their intersection ∩ Un is dense.
Note that neither of these statements implies the other, since there are complete metric spaces which are not locally compact (the irrational number
s with the metric defined below; also, any Banach space of infinite dimension), and there are locally compact Hausdorff space which are not metrizable (for instance, any uncountable product of non-trivial compact Hausdorff spaces is such; also, several function spaces used in Functional Analysis; the uncountable Fort space
). See Steen and Seebach
in the references below.
This formulation is a consequence of BCT1 and is sometimes more useful in applications. Also: if a non-empty complete metric space is the countable union of closed sets, then one of these closed sets has non empty interior.
The restricted form of the Baire category theorem in which the complete metric space is also assumed to be separable is provable in ZF with no additional choice principles. This restricted form applies in particular to the real line, the Baire space
ωω, and the Cantor space
2ω.
to prove the open mapping theorem
, the closed graph theorem
and the uniform boundedness principle
.
BCT1 also shows that every complete metric space with no isolated point
s is uncountable. (If X is a countable complete metric space with no isolated points, then each singleton {x} in X is nowhere dense, and so X is of first category in itself.) In particular, this proves that the set of all real number
s is uncountable.
BCT1 shows that each of the following is a Baire space:
By BCT2, every finite-dimensional Hausdorff manifold
is a Baire space, since it is locally compact and Hausdorff. This is so even for non-paracompact (hence nonmetrizable) manifolds such as the long line
.
 is a Baire space.
is a Baire space.
Let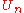 be a countable collection of open dense subsets. We want to show that the intersection
be a countable collection of open dense subsets. We want to show that the intersection 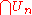 is dense. A subset is dense if and only if every nonempty open subset intersects it. Thus, to show that the intersection is dense, it is sufficient to show that any nonempty open set
is dense. A subset is dense if and only if every nonempty open subset intersects it. Thus, to show that the intersection is dense, it is sufficient to show that any nonempty open set  has a point x in common with all of the
has a point x in common with all of the 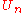 . Since
. Since 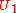 is dense,
is dense,  intersects
intersects 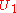 ; thus, there is a point
; thus, there is a point  and
and 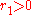 such that:
such that: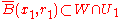 .
.
(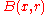 and
and 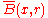 denote an open ball centered at x with radius r and its closure, respectively.) Since
denote an open ball centered at x with radius r and its closure, respectively.) Since 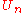 are dense, in a recursive manner, we find a pair of sequences
are dense, in a recursive manner, we find a pair of sequences 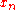 and
and  such that:
such that: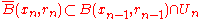 as well as
as well as 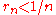 .
.
Since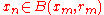 when
when  , we have that
, we have that 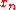 is Cauchy
is Cauchy
, and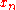 converges to some limit
converges to some limit  by completeness. For any
by completeness. For any  , by closedness,
, by closedness, .
.
Hence,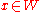 and
and 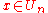 for all
for all  .
. 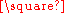
General topology
In mathematics, general topology or point-set topology is the branch of topology which studies properties of topological spaces and structures defined on them...
and functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
. The theorem has two forms, each of which gives sufficient conditions for a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
to be a Baire space
Baire space
In mathematics, a Baire space is a topological space which, intuitively speaking, is very large and has "enough" points for certain limit processes. It is named in honor of René-Louis Baire who introduced the concept.- Motivation :...
.
The theorem was proved by René-Louis Baire
René-Louis Baire
René-Louis Baire was a French mathematician most famous for his Baire category theorem, which helped to generalize and prove future theorems...
in his 1899 doctoral thesis.
Statement of the theorem
A Baire spaceBaire space
In mathematics, a Baire space is a topological space which, intuitively speaking, is very large and has "enough" points for certain limit processes. It is named in honor of René-Louis Baire who introduced the concept.- Motivation :...
is a topological space with the following property: for each countable collection of open
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
dense set
Dense set
In topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
s Un, their intersection ∩ Un is dense.
- (BCT1) Every complete metric space is a Baire space. More generally, every topological space which is homeomorphic to an open subsetOpen setThe concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
of a completeComplete spaceIn mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
pseudometric spacePseudometric spaceIn mathematics, a pseudometric space is a generalized metric space in which the distance between two distinct points can be zero. In the same way as every normed space is a metric space, every seminormed space is a pseudometric space...
is a Baire space. Thus every completely metrizable topological space is a Baire space. - (BCT2) Every locally compact Hausdorff spaceHausdorff spaceIn topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
is a Baire space. The proof is similar to the preceding statement; the finite intersection propertyFinite intersection propertyIn general topology, a branch of mathematics, the finite intersection property is a property of a collection of subsets of a set X. A collection has this property if the intersection over any finite subcollection of the collection is nonempty....
takes the role played by completeness.
Note that neither of these statements implies the other, since there are complete metric spaces which are not locally compact (the irrational number
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
s with the metric defined below; also, any Banach space of infinite dimension), and there are locally compact Hausdorff space which are not metrizable (for instance, any uncountable product of non-trivial compact Hausdorff spaces is such; also, several function spaces used in Functional Analysis; the uncountable Fort space
Fort space
In mathematics, Fort space, named after M. K. Fort, Jr., is an example in the theory of topological spaces.Let X be an infinite set of points, of which P is one...
). See Steen and Seebach
Counterexamples in Topology
Counterexamples in Topology is a book on mathematics by topologists Lynn Steen and J. Arthur Seebach, Jr.In the process of working on problems like the metrization problem, topologists have defined a wide variety of topological properties...
in the references below.
- (BCT3) A non-empty complete metric space is NOT the countable union of nowhere-denseNowhere dense setIn mathematics, a nowhere dense set in a topological space is a set whose closure has empty interior. The order of operations is important. For example, the set of rational numbers, as a subset of R has the property that the closure of the interior is empty, but it is not nowhere dense; in fact it...
sets (i.e., sets whose closure has dense complement).
This formulation is a consequence of BCT1 and is sometimes more useful in applications. Also: if a non-empty complete metric space is the countable union of closed sets, then one of these closed sets has non empty interior.
Relation to the axiom of choice
The proofs of BCT1 and BCT2 for arbitrary complete metric spaces require some form of the axiom of choice; and in fact BCT1 is equivalent over ZF to a weak form of the axiom of choice called the axiom of dependent choices.The restricted form of the Baire category theorem in which the complete metric space is also assumed to be separable is provable in ZF with no additional choice principles. This restricted form applies in particular to the real line, the Baire space
Baire space (set theory)
In set theory, the Baire space is the set of all infinite sequences of natural numbers with a certain topology. This space is commonly used in descriptive set theory, to the extent that its elements are often called “reals.” It is often denoted B, N'N, or ωω...
ωω, and the Cantor space
Cantor space
In mathematics, a Cantor space, named for Georg Cantor, is a topological abstraction of the classical Cantor set: a topological space is a Cantor space if it is homeomorphic to the Cantor set. In set theory, the topological space 2ω is called "the" Cantor space...
2ω.
Uses of the theorem
BCT1 is used in functional analysisFunctional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
to prove the open mapping theorem
Open mapping theorem (functional analysis)
In functional analysis, the open mapping theorem, also known as the Banach–Schauder theorem , is a fundamental result which states that if a continuous linear operator between Banach spaces is surjective then it is an open map...
, the closed graph theorem
Closed graph theorem
In mathematics, the closed graph theorem is a basic result in functional analysis which characterizes continuous linear operators between Banach spaces in terms of the operator graph.- The closed graph theorem :...
and the uniform boundedness principle
Uniform boundedness principle
In mathematics, the uniform boundedness principle or Banach–Steinhaus theorem is one of the fundamental results in functional analysis. Together with the Hahn–Banach theorem and the open mapping theorem, it is considered one of the cornerstones of the field...
.
BCT1 also shows that every complete metric space with no isolated point
Isolated point
In topology, a branch of mathematics, a point x of a set S is called an isolated point of S, if there exists a neighborhood of x not containing other points of S.In particular, in a Euclidean space ,...
s is uncountable. (If X is a countable complete metric space with no isolated points, then each singleton {x} in X is nowhere dense, and so X is of first category in itself.) In particular, this proves that the set of all real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s is uncountable.
BCT1 shows that each of the following is a Baire space:
- The space R of real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s - The irrational numbers, with the metric defined by d(x, y) = 1 / (n + 1), where n is the first index for which the continued fractionContinued fractionIn mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
expansions of x and y differ (this is a complete metric space) - The Cantor setCantor setIn mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
By BCT2, every finite-dimensional Hausdorff manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
is a Baire space, since it is locally compact and Hausdorff. This is so even for non-paracompact (hence nonmetrizable) manifolds such as the long line
Long line (topology)
In topology, the long line is a topological space somewhat similar to the real line, but in a certain way "longer". It behaves locally just like the real line, but has different large-scale properties. Therefore it serves as one of the basic counterexamples of topology...
.
Proof
The following is a standard proof that a complete pseudo-metric space is a Baire space.
is a Baire space.Let
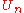 be a countable collection of open dense subsets. We want to show that the intersection
be a countable collection of open dense subsets. We want to show that the intersection 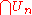 is dense. A subset is dense if and only if every nonempty open subset intersects it. Thus, to show that the intersection is dense, it is sufficient to show that any nonempty open set
is dense. A subset is dense if and only if every nonempty open subset intersects it. Thus, to show that the intersection is dense, it is sufficient to show that any nonempty open set  has a point x in common with all of the
has a point x in common with all of the 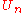 . Since
. Since 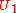 is dense,
is dense,  intersects
intersects 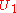 ; thus, there is a point
; thus, there is a point  and
and 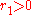 such that:
such that: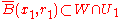 .
.(
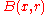 and
and 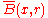 denote an open ball centered at x with radius r and its closure, respectively.) Since
denote an open ball centered at x with radius r and its closure, respectively.) Since 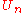 are dense, in a recursive manner, we find a pair of sequences
are dense, in a recursive manner, we find a pair of sequences 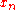 and
and  such that:
such that: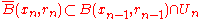 as well as
as well as 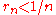 .
.Since
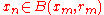 when
when  , we have that
, we have that 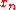 is Cauchy
is CauchyCauchy sequence
In mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses...
, and
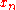 converges to some limit
converges to some limit  by completeness. For any
by completeness. For any  , by closedness,
, by closedness, .
.Hence,
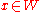 and
and 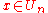 for all
for all  .
.