LF-space
Encyclopedia
In mathematics
, an LF-space is a topological vector space
V that is a countable
strict inductive limit of Fréchet space
s. This means that for each n there is a subspace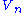
such that
The topology on V is defined by specifying that a convex subset U is a neighborhood of 0 if and only if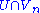
is a neighborhood of 0 in 
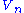for every n.
, bornological
, and ultrabornological.
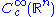, the space of all infinitely differentiable functions on 
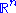with compact support. The LF-space structure is obtained by considering a sequence of compact sets 
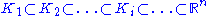with 
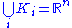and for all i, 
is a subset of the interior of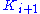 
. Such a sequence could be the balls of radius i centered at the origin. The space 
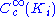of infinitely differentiable functions on 
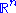with compact support contained in 
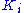has a natural Fréchet space
structure and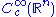
inherits its LF-space structure as described above. The LF-space topology does not depend on the particular sequence of compact sets 
.
With this LF-space structure,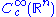
is known as the space of test functions, of fundamental importance in the theory of distributions
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an LF-space is a topological vector space
Topological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
V that is a countable
Countable set
In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
strict inductive limit of Fréchet space
Fréchet space
In functional analysis and related areas of mathematics, Fréchet spaces, named after Maurice Fréchet, are special topological vector spaces. They are generalizations of Banach spaces...
s. This means that for each n there is a subspace
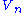such that-
- For all n,
; -
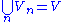; - Each
has a Frechet space structure; - The topology induced on
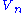by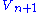 
is identical to the original topology on 
.
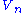- For all n,
The topology on V is defined by specifying that a convex subset U is a neighborhood of 0 if and only if
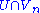is a neighborhood of 0 in 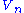for every n.Properties
An LF space is barrelledBarrelled space
In functional analysis and related areas of mathematics, barrelled spaces are Hausdorff topological vector spaces for which every barrelled set in the space is a neighbourhood for the zero vector. A barrelled set or a barrel in a topological vector space is a set which is convex, balanced,...
, bornological
Bornological space
In mathematics, particularly in functional analysis, a bornological space is a type of space which, in some sense, possesses the minimum amount of structure needed to address questions of boundedness of sets and functions, in the same way that a topological space possesses the minimum amount of...
, and ultrabornological.
Examples
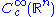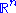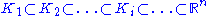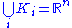A typical example of an LF-space is,, the space of all infinitely differentiable functions on with compact support. The LF-space structure is obtained by considering a sequence of compact sets with and for all i, is a subset of the interior of 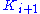. Such a sequence could be the balls of radius i centered at the origin. The space 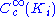of infinitely differentiable functions on 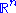with compact support contained in 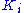has a natural Fréchet spaceFréchet space
In functional analysis and related areas of mathematics, Fréchet spaces, named after Maurice Fréchet, are special topological vector spaces. They are generalizations of Banach spaces...
structure and
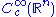inherits its LF-space structure as described above. The LF-space topology does not depend on the particular sequence of compact sets .With this LF-space structure,
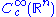is known as the space of test functions, of fundamental importance in the theory of distributionsDistribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
.