
Weak topology
Encyclopedia
In mathematics
, weak topology is an alternative term for initial topology
. The term is most commonly used for the initial topology of a topological vector space
(such as a normed vector space
) with respect to its continuous dual. The remainder of this article will deal with this case, which is one of the basic concepts of functional analysis
.
One may call subsets of a topological vector space weakly closed (respectively, compact, etc.) if they are closed (respectively, compact, etc.) with respect to the weak topology. Likewise, functions are sometimes called weakly continuous (respectively, differentiable, analytic, etc.) if they are continuous (respectively, differentiable
, analytic
, etc.) with respect to the weak topology.
with a topology
such that addition, multiplication, and division are continuous.
In most applications K will be either the field of complex numbers or the field of real number
s with the familiar topologies.
Let X be a topological vector space
over K. Namely, X is a K vector space
equipped with a topology
so that vector addition and scalar multiplication
are continuous.
We may define a possibly different topology on X using the continuous (or topological) dual space
X*. The dual space consists of all linear functions from
X into the base field K which are continuous with respect to the given topology. The weak topology on X is the initial topology
with respect to X*. In other words, it is the
coarsest
topology (the topology with the fewest open sets) such that each element of X* is a continuous function
.
In order to distinguish the weak topology from the original topology on X, the original topology is often called the strong topology.
A subbase
for the weak topology is the collection of sets of the form φ-1(U) where φ ∈ X* and U is an open subset of the base field K.
In other words, a subset of X is open in the weak topology if and only if it can be written as a union of (possibly infinitely many) sets,
each of which is an intersection of finitely many sets of the form φ-1(U).
More generally, if F is a subset of the algebraic dual space, then the initial topology
of X with respect to F, denoted by σ(X,F), is the weak topology with respect to F . If one takes F to be the whole continuous dual space of X, then the weak topology with respect to F coincides with the weak topology defined above.
If the field K has an absolute value
 , then the weak topology σ(X,F) is induced by the family of
, then the weak topology σ(X,F) is induced by the family of
seminorms,

for all f∈F and x∈X. In particular, weak topologies are locally convex.
From this point of view, the weak topology is the coarsest polar topology; see weak topology (polar topology)
for details. Specifically, if F is a vector space of linear functionals on X which separates points of X, then the continuous dual of X with respect to the topology σ(X,F) is precisely equal to F .
(xλ) in X converges in the weak topology to the element x of X if and only if φ(xλ) converges to φ(x) in R or C for all φ in X* .
In particular, if xn is a sequence in X, then xn converges weakly to x if
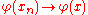
as n → ∞ for all φ ∈ X*. In this case, it is customary to write

or, sometimes,

.
If X is a normed space with norm | ⋅ |. then the dual space X* is itself a normed vector space by using the norm ǁφǁ = supǁxǁ≤1|φ(x)|. This norm gives rise to a topology, called the strong topology, on X*. This is the topology of uniform convergence. The uniform and strong topologies are generally different for other spaces of linear maps; see below.
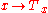
where
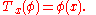
Thus T : X → X** is an injective linear mapping, though it is not surjective unless X is reflexive
. The weak-* topology on X* is the weak topology induced by the image of T: T(X) ⊂ X**. In other words, it is the coarsest topology such that the maps Tx from X* to the base field R or C remain continuous.
φλ in X* is convergent to φ in the weak-* topology if it converges pointwise:
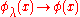
for all x in X. In particular, a sequence of φn ∈ X* converges to φ provided that
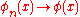
for all x in X. In this case, one writes
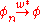
as n → ∞.
Weak-* convergence is sometimes called the topology of simple convergence or the topology of pointwise convergence. Indeed, it coincides with the topology of pointwise convergence
of linear functionals.
(more generally, the polar in X* of a neighborhood of 0 in X is weak*-compact). Moreover, the closed unit ball in a normed space X is compact in the weak topology if and only if X is reflexive.
In more generality, let F be locally compact valued field (e.g., the reals, the complex numbers, or any of the p-adic number systems). Let X be a normed topological vector space over F, compatible with the absolute value in F. Then in X*, the topological dual space X of continuous F-valued linear functionals on X, all norm-closed balls are compact in the weak-* topology.
If a normed space X is separable, then the weak-* topology is separable. It is metrizable on the norm-bounded subsets of X*, although not metrizable on all of X* unless X is finite-dimensional.
L2(Rn)
. Strong convergence of a sequence ψk∈L2(Rn) to an element ψ means that
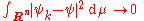
as k→∞. Here the notion of convergence corresponds to the norm on L2.
In contrast weak convergence only demands that

for all functions f∈L2 (or, more typically, all f in a dense subset of L2 such as a space of test functions). For given test functions, the relevant notion of convergence only corresponds to the topology used in C.
For example, in the Hilbert space L2(0,π), the sequence of functions

form an orthonormal basis
. In particular, the (strong) limit of ψk as k→∞ does not exist. On the other hand, by the Riemann–Lebesgue lemma, the weak limit exists and is zero.
by forming the strong dual of a space of test functions (such as the compactly supported smooth functions on Rn). In an alternative construction of such spaces, one can take the weak dual of a space of test functions inside a Hilbert space such as L2. Thus one is led to consider the idea of a rigged Hilbert space
.
s f:X → Y may carry a variety of different possible topologies. The naming of such topologies depends on the kind of topology one is using on the target space Y to define operator convergence . There are, in general, a vast array of possible operator topologies
on L(X,Y), whose naming is not entirely intuitive.
For example, the strong operator topology
on L(X,Y) is the topology of pointwise convergence. For instance, if Y is a normed space, then this topology is defined by the seminorms indexed by x∈X:
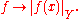
More generally, if a family of seminorms Q defines the topology on Y, then the seminorms pq,x on L(X,Y) defining the strong topology are given by

indexed by q∈Q and x∈X.
In particular, see the weak operator topology
and weak* operator topology.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, weak topology is an alternative term for initial topology
Initial topology
In general topology and related areas of mathematics, the initial topology on a set X, with respect to a family of functions on X, is the coarsest topology on X which makes those functions continuous.The subspace topology and product topology constructions are both special cases of initial...
. The term is most commonly used for the initial topology of a topological vector space
Topological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
(such as a normed vector space
Normed vector space
In mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
) with respect to its continuous dual. The remainder of this article will deal with this case, which is one of the basic concepts of functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
.
One may call subsets of a topological vector space weakly closed (respectively, compact, etc.) if they are closed (respectively, compact, etc.) with respect to the weak topology. Likewise, functions are sometimes called weakly continuous (respectively, differentiable, analytic, etc.) if they are continuous (respectively, differentiable
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
, analytic
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
, etc.) with respect to the weak topology.
The weak and strong topologies
Let K be a topological field, namely a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
with a topology
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
such that addition, multiplication, and division are continuous.
In most applications K will be either the field of complex numbers or the field of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s with the familiar topologies.
Let X be a topological vector space
Topological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
over K. Namely, X is a K vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
equipped with a topology
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
so that vector addition and scalar multiplication
Scalar multiplication
In mathematics, scalar multiplication is one of the basic operations defining a vector space in linear algebra . In an intuitive geometrical context, scalar multiplication of a real Euclidean vector by a positive real number multiplies the magnitude of the vector without changing its direction...
are continuous.
We may define a possibly different topology on X using the continuous (or topological) dual space
Dual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
X*. The dual space consists of all linear functions from
X into the base field K which are continuous with respect to the given topology. The weak topology on X is the initial topology
Initial topology
In general topology and related areas of mathematics, the initial topology on a set X, with respect to a family of functions on X, is the coarsest topology on X which makes those functions continuous.The subspace topology and product topology constructions are both special cases of initial...
with respect to X*. In other words, it is the
coarsest
Comparison of topologies
In topology and related areas of mathematics comparison of topologies refers to the fact that two topological structures on a given set may stand in relation to each other. The set of all possible topologies on a given set forms a partially ordered set...
topology (the topology with the fewest open sets) such that each element of X* is a continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
.
In order to distinguish the weak topology from the original topology on X, the original topology is often called the strong topology.
A subbase
Subbase
In topology, a subbase for a topological space X with topology T is a subcollection B of T which generates T, in the sense that T is the smallest topology containing B...
for the weak topology is the collection of sets of the form φ-1(U) where φ ∈ X* and U is an open subset of the base field K.
In other words, a subset of X is open in the weak topology if and only if it can be written as a union of (possibly infinitely many) sets,
each of which is an intersection of finitely many sets of the form φ-1(U).
More generally, if F is a subset of the algebraic dual space, then the initial topology
Initial topology
In general topology and related areas of mathematics, the initial topology on a set X, with respect to a family of functions on X, is the coarsest topology on X which makes those functions continuous.The subspace topology and product topology constructions are both special cases of initial...
of X with respect to F, denoted by σ(X,F), is the weak topology with respect to F . If one takes F to be the whole continuous dual space of X, then the weak topology with respect to F coincides with the weak topology defined above.
If the field K has an absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
 , then the weak topology σ(X,F) is induced by the family of
, then the weak topology σ(X,F) is induced by the family ofseminorms,

for all f∈F and x∈X. In particular, weak topologies are locally convex.
From this point of view, the weak topology is the coarsest polar topology; see weak topology (polar topology)
Weak topology (polar topology)
In functional analysis and related areas of mathematics the weak topology is the coarsest polar topology, the topology with the fewest open sets, on a dual pair...
for details. Specifically, if F is a vector space of linear functionals on X which separates points of X, then the continuous dual of X with respect to the topology σ(X,F) is precisely equal to F .
Weak convergence
The weak topology is characterized by the following condition: a netNet (mathematics)
In mathematics, more specifically in general topology and related branches, a net or Moore–Smith sequence is a generalization of the notion of a sequence. In essence, a sequence is a function with domain the natural numbers, and in the context of topology, the range of this function is...
(xλ) in X converges in the weak topology to the element x of X if and only if φ(xλ) converges to φ(x) in R or C for all φ in X* .
In particular, if xn is a sequence in X, then xn converges weakly to x if
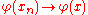
as n → ∞ for all φ ∈ X*. In this case, it is customary to write

or, sometimes,

Other properties
If X is equipped with the weak topology, then addition and scalar multiplication remain continuous operations, and X is a locally convex topological vector spaceLocally convex topological vector space
In functional analysis and related areas of mathematics, locally convex topological vector spaces or locally convex spaces are examples of topological vector spaces which generalize normed spaces. They can be defined as topological vector spaces whose topology is generated by translations of ...
.
If X is a normed space with norm | ⋅ |. then the dual space X* is itself a normed vector space by using the norm ǁφǁ = supǁxǁ≤1|φ(x)|. This norm gives rise to a topology, called the strong topology, on X*. This is the topology of uniform convergence. The uniform and strong topologies are generally different for other spaces of linear maps; see below.
The weak-* topology
A space X can be embedded into the double dual X** by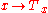
where
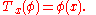
Thus T : X → X** is an injective linear mapping, though it is not surjective unless X is reflexive
Reflexive space
In functional analysis, a Banach space is called reflexive if it coincides with the dual of its dual space in the topological and algebraic senses. Reflexive Banach spaces are often characterized by their geometric properties.- Normed spaces :Suppose X is a normed vector space over R or C...
. The weak-* topology on X* is the weak topology induced by the image of T: T(X) ⊂ X**. In other words, it is the coarsest topology such that the maps Tx from X* to the base field R or C remain continuous.
Weak-* convergence
A netNet (mathematics)
In mathematics, more specifically in general topology and related branches, a net or Moore–Smith sequence is a generalization of the notion of a sequence. In essence, a sequence is a function with domain the natural numbers, and in the context of topology, the range of this function is...
φλ in X* is convergent to φ in the weak-* topology if it converges pointwise:
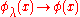
for all x in X. In particular, a sequence of φn ∈ X* converges to φ provided that
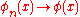
for all x in X. In this case, one writes
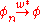
as n → ∞.
Weak-* convergence is sometimes called the topology of simple convergence or the topology of pointwise convergence. Indeed, it coincides with the topology of pointwise convergence
Pointwise convergence
In mathematics, pointwise convergence is one of various senses in which a sequence of functions can converge to a particular function.-Definition:...
of linear functionals.
Other properties
By definition, the weak* topology is weaker than the weak topology on X*. An important fact about the weak* topology is the Banach–Alaoglu theorem: if X is normed, then the closed unit ball in X* is weak*-compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
(more generally, the polar in X* of a neighborhood of 0 in X is weak*-compact). Moreover, the closed unit ball in a normed space X is compact in the weak topology if and only if X is reflexive.
In more generality, let F be locally compact valued field (e.g., the reals, the complex numbers, or any of the p-adic number systems). Let X be a normed topological vector space over F, compatible with the absolute value in F. Then in X*, the topological dual space X of continuous F-valued linear functionals on X, all norm-closed balls are compact in the weak-* topology.
If a normed space X is separable, then the weak-* topology is separable. It is metrizable on the norm-bounded subsets of X*, although not metrizable on all of X* unless X is finite-dimensional.
Hilbert spaces
Consider, for example, the difference between strong and weak convergence of functions in the Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
L2(Rn)
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
. Strong convergence of a sequence ψk∈L2(Rn) to an element ψ means that
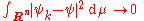
as k→∞. Here the notion of convergence corresponds to the norm on L2.
In contrast weak convergence only demands that

for all functions f∈L2 (or, more typically, all f in a dense subset of L2 such as a space of test functions). For given test functions, the relevant notion of convergence only corresponds to the topology used in C.
For example, in the Hilbert space L2(0,π), the sequence of functions

form an orthonormal basis
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
. In particular, the (strong) limit of ψk as k→∞ does not exist. On the other hand, by the Riemann–Lebesgue lemma, the weak limit exists and is zero.
Distributions
One normally obtains spaces of distributionsDistribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
by forming the strong dual of a space of test functions (such as the compactly supported smooth functions on Rn). In an alternative construction of such spaces, one can take the weak dual of a space of test functions inside a Hilbert space such as L2. Thus one is led to consider the idea of a rigged Hilbert space
Rigged Hilbert space
In mathematics, a rigged Hilbert space is a construction designed to link the distribution and square-integrable aspects of functional analysis. Such spaces were introduced to study spectral theory in the broad sense...
.
Operator topologies
If X and Y are topological vector spaces, the space L(X,Y) of continuous linear operatorContinuous linear operator
In functional analysis and related areas of mathematics, a continuous linear operator or continuous linear mapping is a continuous linear transformation between topological vector spaces....
s f:X → Y may carry a variety of different possible topologies. The naming of such topologies depends on the kind of topology one is using on the target space Y to define operator convergence . There are, in general, a vast array of possible operator topologies
Operator topology
In the mathematical field of functional analysis there are several standard topologies which are given to the algebra B of bounded linear operators on a Hilbert space H.-Introduction:...
on L(X,Y), whose naming is not entirely intuitive.
For example, the strong operator topology
Strong operator topology
In functional analysis, a branch of mathematics, the strong operator topology, often abbreviated SOT, is the weakest locally convex topology on the set of bounded operators on a Hilbert space such that the evaluation map sending an operator T to the real number \|Tx\| is continuous for each vector...
on L(X,Y) is the topology of pointwise convergence. For instance, if Y is a normed space, then this topology is defined by the seminorms indexed by x∈X:
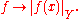
More generally, if a family of seminorms Q defines the topology on Y, then the seminorms pq,x on L(X,Y) defining the strong topology are given by

indexed by q∈Q and x∈X.
In particular, see the weak operator topology
Weak operator topology
In functional analysis, the weak operator topology, often abbreviated WOT, is the weakest topology on the set of bounded operators on a Hilbert space H, such that the functional sending an operator T to the complex number is continuous for any vectors x and y in the Hilbert space.Equivalently, a...
and weak* operator topology.
See also
- Weak convergence (Hilbert space)Weak convergence (Hilbert space)In mathematics, weak convergence in a Hilbert space is convergence of a sequence of points in the weak topology.-Definition:A sequence of points in a Hilbert space H is said to converge weakly to a point x in H if...
- Weak-star operator topology
- Weak convergence of measures
- Topologies on the set of operators on a Hilbert space
- Vague topologyVague topologyIn mathematics, particularly in the area of functional analysis and topological vector spaces, the vague topology is an example of the weak-* topology which arises in the study of measures on locally compact Hausdorff spaces....

