Cantor–Bernstein–Schroeder theorem
Encyclopedia
In set theory
, the Cantor–Bernstein–Schroeder theorem
, named after Georg Cantor
, Felix Bernstein
, and Ernst Schröder
, states that, if there exist injective function
s and between the sets A and B, then there exists a bijective
function . In terms of the cardinality of the two sets, this means that if |A| ≤ |B| and |B| ≤ |A|, then |A| = |B|; that is, A and B are equipollent. This is a useful feature in the ordering of cardinal number
s.
The theorem is also known as the Schroeder–Bernstein theorem, the Cantor–Bernstein theorem, or the Cantor–Schroeder–Bernstein theorem.
An important feature of this theorem is that it does not rely on the axiom of choice.
.
Assume without loss of generality that A and B are disjoint. For any a in A or b in B we can form a unique two-sided sequence of elements that are alternately in A and B, by repeatedly applying
and 
to go right and 
and 
to go left (where defined).
For any particular a, this sequence may terminate to the left or not, at a point where
or 
is not defined.
Call such a sequence (and all its elements) an A-stopper, if it stops at an element of A, or a B-stopper if it stops at an element of B. Otherwise, call it doubly infinite if all the elements are distinct or cyclic if it repeats.
By the fact that
and 
are injective functions, each a in A and b in B is in exactly one such sequence to within identity, (as if an element occurs in two sequences, all elements to the left and to the right must be the same in both, by definition).
By the above observation, the sequences form a partition
of the whole of the disjoint union of A and B, hence it suffices to produce a bijection between the elements of A and B in each of the sequences separately.
For an A-stopper, the function
is a bijection between its elements in A and its elements in B.
For a B-stopper, the function
is a bijection between its elements in B and its elements in A.
For a doubly infinite sequence or a cyclic sequence, either
or 
will do.
In the alternate proof,
can be interpreted as the set of n-th elements of A-stoppers (starting from 0).
Indeed,
is the set of elements for which 
is not defined, which is the set of starting elements of A-stoppers, 
is the set of elements for which 
is defined but 
is not, i.e. the set of second elements of A-stoppers, and so on.
The bijection
is defined as 
on 
and 
everywhere else, which means 
on A-stoppers and 
everywhere else, consistently with the proof below.
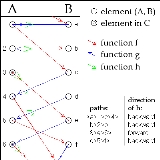
Displayed are parts of the (disjoint) sets A and B together with parts of the mappings f and g. If the set A ∪ B, together with the two maps, is interpreted as a directed graph, then this bipartite graph has several connected components.
These can be divided into four types: paths extending infinitely to both directions, finite cycles of even length, infinite paths starting in the set A, and infinite paths starting in the set B (the path passing through the element a in the diagram is infinite in both directions, so the diagram contains one path of every type). In general, it is not possible to decide in a finite number of steps which type of path a given element of A or B belongs to.
The set C defined above contains precisely the elements of A which are part of an infinite path starting in A. The map h is then defined in such a way that for every path it yields a bijection that maps each element of A in the path to an element of B directly before or after it in the path. For the path that is infinite in both directions, and for the finite cycles, we choose to map every element to its predecessor in the path.
Idea of the proof: Redefine f in certain points to make it surjective. At first, redefine it on the image of g for it to be the inverse function
of g. However, this might destroy injectivity, so correct this problem iteratively, by making the amount of points redefined smaller, up to a minimum possible, shifting the problem "to infinity" and therefore out of sight.
More precisely, this means to leave f unchanged initially on C0 := A \ g[ B] . However, then every element of f[ C0] has two preimages, one under f and one under g –1. Therefore, leave f unchanged on the union
of C0 and C1 := g[ f[ C0]] . However, then every element of f[ C1] has two preimages, correct this by leaving f unchanged on the union of C0, C1, and C2 := g[ f[ C1]] and so on. Leaving f unchanged on the countable union C of C0 and all these Cn+1 = g[ f[ Cn]] solves the problem, because g[ f[ C]] is a subset of C and no additional union is necessary.
Proof: Define
and
Then, for every a ∈ A define
If a is not in C, then, in particular, a is not in C0. Hence a ∈ g[ B] by the definition of C0. Since g is injective, its preimage g –1(a) is therefore well defined.
It remains to check the following properties of the map h : A → B to verify that it is the desired bijection:
Note that the above definition of h is nonconstructive, in the sense that there exists no general method to decide in a finite number of steps, for any given sets A and B and injections f and g, whether an element a of A does not lie in C. For special sets and maps this might, of course, be possible.
relied, in effect, on the axiom of choice by inferring the result as a corollary
of the well-ordering theorem
. The argument given above shows that the result can be proved without using the axiom of choice.
Furthermore, there is a simple proof which uses Tarski's fixed point theorem
.
The traditional name "Schröder-Bernstein" is based on two proofs published independently in 1898.
Cantor is often added because he first stated the theorem in 1895,
while Schröder's name is often omitted because his proof turned out to be flawed
while the name of the mathematician who first proved it is not connected with the theorem.
In reality, the history was more complicated:
Both proofs of Dedekind are based on his famous memoir Was sind und was sollen die Zahlen?
and derive it as a corollary of a proposition equivalent to statement C in Cantor's paper:
Cantor observed this property as early as 1882/83 during his studies in set theory and transfinite numbers
and therefore (implicitly) relying on the Axiom of Choice.
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, the Cantor–Bernstein–Schroeder theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
, named after Georg Cantor
Georg Cantor
Georg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...
, Felix Bernstein
Felix Bernstein
Felix Bernstein was a German Jewish mathematician known for developing a theorem of the equivalence of sets in 1897, and less well known for demonstrating the correct blood group inheritance pattern of multiple alleles at one locus in 1924 through statistical analysis...
, and Ernst Schröder
Ernst Schröder
Ernst Schröder was a German mathematician mainly known for his work on algebraic logic. He is a major figure in the history of mathematical logic , by virtue of summarizing and extending the work of George Boole, Augustus De Morgan, Hugh MacColl, and especially Charles Peirce...
, states that, if there exist injective function
Injective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
s and between the sets A and B, then there exists a bijective
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
function . In terms of the cardinality of the two sets, this means that if |A| ≤ |B| and |B| ≤ |A|, then |A| = |B|; that is, A and B are equipollent. This is a useful feature in the ordering of cardinal number
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
s.
The theorem is also known as the Schroeder–Bernstein theorem, the Cantor–Bernstein theorem, or the Cantor–Schroeder–Bernstein theorem.
An important feature of this theorem is that it does not rely on the axiom of choice.
Proof
This proof is attributed to Julius KönigJulius König
Gyula Kőnig was a Hungarian mathematician. He was born in Győr, Hungary and died in Budapest. His mathematical publications in foreign languages appeared under the name Julius König...
.
Assume without loss of generality that A and B are disjoint. For any a in A or b in B we can form a unique two-sided sequence of elements that are alternately in A and B, by repeatedly applying
and to go right and and to go left (where defined).For any particular a, this sequence may terminate to the left or not, at a point where
or is not defined.Call such a sequence (and all its elements) an A-stopper, if it stops at an element of A, or a B-stopper if it stops at an element of B. Otherwise, call it doubly infinite if all the elements are distinct or cyclic if it repeats.
By the fact that
and are injective functions, each a in A and b in B is in exactly one such sequence to within identity, (as if an element occurs in two sequences, all elements to the left and to the right must be the same in both, by definition).By the above observation, the sequences form a partition
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
of the whole of the disjoint union of A and B, hence it suffices to produce a bijection between the elements of A and B in each of the sequences separately.
For an A-stopper, the function
is a bijection between its elements in A and its elements in B.For a B-stopper, the function
is a bijection between its elements in B and its elements in A.For a doubly infinite sequence or a cyclic sequence, either
or will do.In the alternate proof,
can be interpreted as the set of n-th elements of A-stoppers (starting from 0).Indeed,
is the set of elements for which is not defined, which is the set of starting elements of A-stoppers, is the set of elements for which is defined but is not, i.e. the set of second elements of A-stoppers, and so on.The bijection
is defined as on and everywhere else, which means on A-stoppers and everywhere else, consistently with the proof below.Visualization
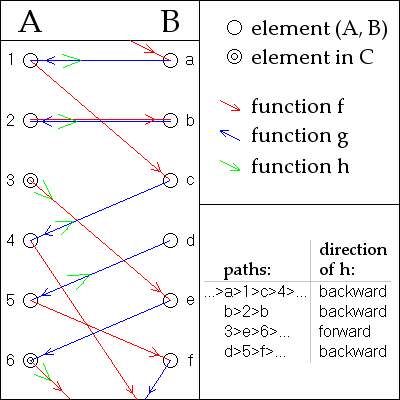
The definition of h can be visualized with the following diagram.Displayed are parts of the (disjoint) sets A and B together with parts of the mappings f and g. If the set A ∪ B, together with the two maps, is interpreted as a directed graph, then this bipartite graph has several connected components.
These can be divided into four types: paths extending infinitely to both directions, finite cycles of even length, infinite paths starting in the set A, and infinite paths starting in the set B (the path passing through the element a in the diagram is infinite in both directions, so the diagram contains one path of every type). In general, it is not possible to decide in a finite number of steps which type of path a given element of A or B belongs to.
The set C defined above contains precisely the elements of A which are part of an infinite path starting in A. The map h is then defined in such a way that for every path it yields a bijection that maps each element of A in the path to an element of B directly before or after it in the path. For the path that is infinite in both directions, and for the finite cycles, we choose to map every element to its predecessor in the path.
Alternate proof
Below follows an alternate proof.Idea of the proof: Redefine f in certain points to make it surjective. At first, redefine it on the image of g for it to be the inverse function
Inverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
of g. However, this might destroy injectivity, so correct this problem iteratively, by making the amount of points redefined smaller, up to a minimum possible, shifting the problem "to infinity" and therefore out of sight.
More precisely, this means to leave f unchanged initially on C0 := A \ g
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of C0 and C1 := g
Proof: Define
and
Then, for every a ∈ A define
If a is not in C, then, in particular, a is not in C0. Hence a ∈ g
It remains to check the following properties of the map h : A → B to verify that it is the desired bijection:
- Surjectivity: Consider any b ∈ B. If b ∈ f
[ C] , then there is an a ∈ C with b = f(a). Hence b = h(a) by the definition of h. If b is not in f[ C] , define a = g(b). By definition of C0, this a cannot be in C0. Since f[ Cn] is a subset of f[ C] , it follows that b is not in any f[ Cn] , hence a = g(b) is not in any Cn+1 = g[ f[ Cn]] by the recursive definition of these sets. Therefore, a is not in C. Then b = g –1(a) = h(a) by the definition of h.
- Injectivity: Since f is injective on A, which comprises C, and g –1 is injective on g
[ B] , which comprises the complement of C, it suffices to show that the assumption f(c) = g –1(a) for c ∈ C and a ∈ A \ C leads to a contradiction (this means the original problem, the lack of injectivity mentioned in the idea of the proof above, is solved by the clever definition of h). Since c ∈ C, there exists an integer n ≥ 0 such that c ∈ Cn. Hence g(f(c)) is in Cn+1 and therefore in C, too. However, g(f(c)) = g(g –1(a)) = a is not in C — contradiction.
Note that the above definition of h is nonconstructive, in the sense that there exists no general method to decide in a finite number of steps, for any given sets A and B and injections f and g, whether an element a of A does not lie in C. For special sets and maps this might, of course, be possible.
Original proof
An earlier proof by CantorGeorg Cantor
Georg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...
relied, in effect, on the axiom of choice by inferring the result as a corollary
Corollary
A corollary is a statement that follows readily from a previous statement.In mathematics a corollary typically follows a theorem. The use of the term corollary, rather than proposition or theorem, is intrinsically subjective...
of the well-ordering theorem
Well-ordering theorem
In mathematics, the well-ordering theorem states that every set can be well-ordered. A set X is well-ordered by a strict total order if every non-empty subset of X has a least element under the ordering. This is also known as Zermelo's theorem and is equivalent to the Axiom of Choice...
. The argument given above shows that the result can be proved without using the axiom of choice.
Furthermore, there is a simple proof which uses Tarski's fixed point theorem
Knaster–Tarski theorem
In the mathematical areas of order and lattice theory, the Knaster–Tarski theorem, named after Bronisław Knaster and Alfred Tarski, states the following:...
.
History
As it is often the case in mathematics, the name of this theorem does not truly reflect its history.The traditional name "Schröder-Bernstein" is based on two proofs published independently in 1898.
Cantor is often added because he first stated the theorem in 1895,
while Schröder's name is often omitted because his proof turned out to be flawed
while the name of the mathematician who first proved it is not connected with the theorem.
In reality, the history was more complicated:
- 1887 Richard DedekindRichard DedekindJulius Wilhelm Richard Dedekind was a German mathematician who did important work in abstract algebra , algebraic number theory and the foundations of the real numbers.-Life:...
proves the theorem but does not publish it. - 1895 Georg CantorGeorg CantorGeorg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...
states the theorem in his first paper on set theory and transfinite numbers (as an easy consequence of the linear order of cardinal numbers which he was going to prove later). - 1896 Ernst SchröderErnst SchröderErnst Schröder was a German mathematician mainly known for his work on algebraic logic. He is a major figure in the history of mathematical logic , by virtue of summarizing and extending the work of George Boole, Augustus De Morgan, Hugh MacColl, and especially Charles Peirce...
announces a proof (as a corollary of a more general statement). - 1897 Felix BernsteinFelix BernsteinFelix Bernstein was a German Jewish mathematician known for developing a theorem of the equivalence of sets in 1897, and less well known for demonstrating the correct blood group inheritance pattern of multiple alleles at one locus in 1924 through statistical analysis...
, a young student in Cantor's Seminar, presents his proof. - 1897 After a visit by Bernstein, Dedekind independently proves it a second time.
- 1898 Bernstein's proof is published by Émile BorelÉmile BorelFélix Édouard Justin Émile Borel was a French mathematician and politician.Borel was born in Saint-Affrique, Aveyron. Along with René-Louis Baire and Henri Lebesgue, he was among the pioneers of measure theory and its application to probability theory. The concept of a Borel set is named in his...
in his book on functions. (Communicated by Cantor at the 1897 congress in Zürich.)
Both proofs of Dedekind are based on his famous memoir Was sind und was sollen die Zahlen?
and derive it as a corollary of a proposition equivalent to statement C in Cantor's paper:
Cantor observed this property as early as 1882/83 during his studies in set theory and transfinite numbers
and therefore (implicitly) relying on the Axiom of Choice.
See also
- Schröder–Bernstein theorem for measurable spaces
- Schröder–Bernstein theorems for operator algebrasSchröder–Bernstein theorems for operator algebrasThe Schröder–Bernstein theorem, from set theory, has analogs in the context operator algebras. This article discusses such operator-algebraic results.- For von Neumann algebras :...
- Schröder–Bernstein propertySchröder–Bernstein propertyA Schröder–Bernstein property is any mathematical property that matches the following patternThe name Schröder–Bernstein property is in analogy to the theorem of the same name ....
External links
- Citizendium: Schröder-Bernstein theorem and Schröder–Bernstein property