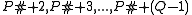Prime gap
Encyclopedia
A prime gap is the difference between two successive prime number
s. The n-th prime gap, denoted gn, is the difference between the (n + 1)-th and the n-th prime number, i.e.
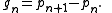
We have g1 = 1, g2 = g3 = 2, and g4 = 4. The sequence (gn) of prime gaps has been extensively studied. One also writes g(pn) for gn.
The first 30 prime gaps are:
, that is, the product
of all prime numbers up to and including P. If Q is the prime number following P, then the sequence
is a sequence of Q − 2 consecutive composite integers, so here there is a prime gap of at least length Q − 1. Therefore, there exist gaps between primes which are arbitrarily large, i.e., for any prime number P, there is an integer n with gn ≥ P. (This is seen by choosing n so that pn is the greatest prime number less than P# + 2.) Another way to see that arbitrarily large prime gaps must exist is the fact that the density of primes approaches zero, according to the Prime number theorem
.
In reality, prime gaps of P numbers can occur at numbers much smaller than P#. For instance, the smallest sequence of 71 consecutive composite numbers occurs between 31398 and 31468, whereas 71# has twenty-seven digits - its full decimal
expansion being 557940830126698960967415390.
Although the average gap between primes increases as the natural logarithm
of the integer, the ratio of the maximum prime gap to the integers involved also increases as larger and larger numbers and gaps are encountered.
In the opposite direction, the twin prime conjecture asserts that gn = 2 for infinitely many integers n.
gap ends has length 2254930, with 86853-digit probable primes found by H. Rosenthal and J. K. Andersen. The largest known prime gap with identified proven primes as gap ends has length 337446, with 7996-digit primes found by T. Alm, J. K. Andersen and François Morain.
We say that gn is a maximal gap if gm < gn for all m < n.
the largest known maximal gap has length 1476, found by Tomás Oliveira e Silva. It is the 75th maximal gap, and it occurs after the prime 1425172824437699411.
The largest known value of gn / ln(pn) is 1476 / ln(1425172824437699411) ≈ 35.31. Usually this number is called the merit of the gap gn .
The prime number theorem
says that the "average length" of the gap between a prime p and the next prime is ln p. The actual length of the gap might be much more or less than this. However, from the prime number theorem one can also deduce an upper bound on the length of prime gaps: for every ε > 0, there is a number N such that gn < εpn for all n > N.
Hoheisel
was the first to show that there exists a constant θ < 1 such that
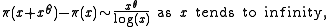
hence showing that
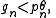
for sufficiently large n.
One can deduce that the gaps get arbitrarily smaller in proportion to the primes: the quotient gn/pn approaches
zero as n goes to infinity.
Hoheisel obtained the possible value 32999/33000 for θ. This was improved to 249/250 by Heilbronn
, and to θ = 3/4 + ε, for any ε > 0, by Chudakov
.
A major improvement is due to Ingham
, who showed that if
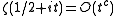
for some positive constant c, where O refers to the big O notation
, then
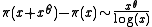
for any θ > (1 + 4c)/(2 + 4c). Here, as usual, ζ denotes the Riemann zeta function and π the prime-counting function. Knowing that any c > 1/6 is admissible, one obtains that θ may be any number greater than 5/8.
An immediate consequence of Ingham's result is that there is always a prime number between n3 and (n + 1)3 if n is sufficiently large. Note however that not even the Lindelöf hypothesis, which assumes that we can take c to be any positive number, implies that there is a prime number between n2 and (n + 1)2, if n is sufficiently large (see Legendre's conjecture
). To verify this, a stronger result such as Cramér's conjecture would be needed.
Huxley
showed that one may choose θ = 7/12.
A recent result, due to Baker, Harman
and Pintz
, shows that θ may be taken to be 0.525.
In 2005, Daniel Goldston
, János Pintz
and Cem Yıldırım
have proved that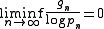
proved the existence of a constant c > 0 such that the inequality
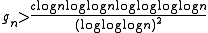
holds for infinitely many values n. The best known value of the constant c is currently c = 2eγ, where γ is the Euler–Mascheroni constant. Paul Erdős
offered a $5,000 prize for a proof or disproof that the constant c in the above inequality may be taken arbitrarily large.
is true. Harald Cramér
proved that, under this assumption, the gap g(pn) satisfies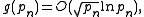
using the big O notation
.
Later, he conjectured that the gaps are even smaller. Roughly speaking he conjectured that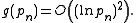
At the moment, the numerical evidence seems to point in this direction. See Cramér's conjecture for more details.
Andrica's conjecture states that
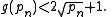
This is a slight strengthening of Legendre's conjecture
that between successive square numbers there is always a prime.
. In this context it is usually denoted dn and called the prime difference function. The function is neither multiplicative
nor additive
.
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s. The n-th prime gap, denoted gn, is the difference between the (n + 1)-th and the n-th prime number, i.e.
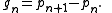
We have g1 = 1, g2 = g3 = 2, and g4 = 4. The sequence (gn) of prime gaps has been extensively studied. One also writes g(pn) for gn.
The first 30 prime gaps are:
- 1, 2, 2, 4, 2, 4, 2, 4, 6, 2, 6, 4, 2, 4, 6, 6, 2, 6, 4, 2, 6, 4, 6, 8, 4, 2, 4, 2, 4, 14 .
Simple observations
For any prime number P, we write P# for P primorialPrimorial
In mathematics, and more particularly in number theory, primorial is a function from natural numbers to natural numbers similar to the factorial function, but rather than multiplying successive positive integers, only successive prime numbers are multiplied...
, that is, the product
Product (mathematics)
In mathematics, a product is the result of multiplying, or an expression that identifies factors to be multiplied. The order in which real or complex numbers are multiplied has no bearing on the product; this is known as the commutative law of multiplication...
of all prime numbers up to and including P. If Q is the prime number following P, then the sequence
is a sequence of Q − 2 consecutive composite integers, so here there is a prime gap of at least length Q − 1. Therefore, there exist gaps between primes which are arbitrarily large, i.e., for any prime number P, there is an integer n with gn ≥ P. (This is seen by choosing n so that pn is the greatest prime number less than P# + 2.) Another way to see that arbitrarily large prime gaps must exist is the fact that the density of primes approaches zero, according to the Prime number theorem
Prime number theorem
In number theory, the prime number theorem describes the asymptotic distribution of the prime numbers. The prime number theorem gives a general description of how the primes are distributed amongst the positive integers....
.
In reality, prime gaps of P numbers can occur at numbers much smaller than P#. For instance, the smallest sequence of 71 consecutive composite numbers occurs between 31398 and 31468, whereas 71# has twenty-seven digits - its full decimal
Decimal
The decimal numeral system has ten as its base. It is the numerical base most widely used by modern civilizations....
expansion being 557940830126698960967415390.
Although the average gap between primes increases as the natural logarithm
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
of the integer, the ratio of the maximum prime gap to the integers involved also increases as larger and larger numbers and gaps are encountered.
In the opposite direction, the twin prime conjecture asserts that gn = 2 for infinitely many integers n.
Numerical results
the largest known prime gap with identified probable primeProbable prime
In number theory, a probable prime is an integer that satisfies a specific condition also satisfied by all prime numbers. Different types of probable primes have different specific conditions...
gap ends has length 2254930, with 86853-digit probable primes found by H. Rosenthal and J. K. Andersen. The largest known prime gap with identified proven primes as gap ends has length 337446, with 7996-digit primes found by T. Alm, J. K. Andersen and François Morain.
We say that gn is a maximal gap if gm < gn for all m < n.
the largest known maximal gap has length 1476, found by Tomás Oliveira e Silva. It is the 75th maximal gap, and it occurs after the prime 1425172824437699411.
The largest known value of gn / ln(pn) is 1476 / ln(1425172824437699411) ≈ 35.31. Usually this number is called the merit of the gap gn .
EWLINE
|
EWLINE
|
EWLINE
|
Upper bounds
Bertrand's postulate states that there is always a prime number between k and 2k, so in particular pn+1 < 2pn, which means gn < pn.The prime number theorem
Prime number theorem
In number theory, the prime number theorem describes the asymptotic distribution of the prime numbers. The prime number theorem gives a general description of how the primes are distributed amongst the positive integers....
says that the "average length" of the gap between a prime p and the next prime is ln p. The actual length of the gap might be much more or less than this. However, from the prime number theorem one can also deduce an upper bound on the length of prime gaps: for every ε > 0, there is a number N such that gn < εpn for all n > N.
Hoheisel
Guido Hoheisel
Guido Hoheisel was a German mathematician, a professor of mathematics at the University of Cologne. He did his PhD in 1920 from the University of Berlin under the supervision of Erhard Schmidt....
was the first to show that there exists a constant θ < 1 such that
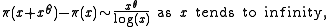
hence showing that
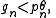
for sufficiently large n.
One can deduce that the gaps get arbitrarily smaller in proportion to the primes: the quotient gn/pn approaches
Limit (mathematics)
In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...
zero as n goes to infinity.
Hoheisel obtained the possible value 32999/33000 for θ. This was improved to 249/250 by Heilbronn
Hans Heilbronn
Hans Arnold Heilbronn was a mathematician.He was born into a German-Jewish family. He was a student at the universities of Berlin, Freiburg and Göttingen, where he met Edmund Landau, who supervised his doctorate...
, and to θ = 3/4 + ε, for any ε > 0, by Chudakov
Nikolai Chudakov
Nikolai Grigor'evich Chudakov was a Russian and Soviet mathematician. He was born in Lysovsk, Novo-Burassk, Saratov, Russian Empire. His father worked as a medical assistant....
.
A major improvement is due to Ingham
Albert Ingham
Albert Edward Ingham was an English mathematician.Ingham was born in Northampton. He went to Stafford Grammar School and Trinity College, Cambridge . He obtained his Ph.D., which was supervised by John Edensor Littlewood, from the University of Cambridge. He supervised the Ph.D.s of C. Brian...
, who showed that if
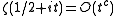
for some positive constant c, where O refers to the big O notation
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
, then
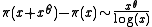
for any θ > (1 + 4c)/(2 + 4c). Here, as usual, ζ denotes the Riemann zeta function and π the prime-counting function. Knowing that any c > 1/6 is admissible, one obtains that θ may be any number greater than 5/8.
An immediate consequence of Ingham's result is that there is always a prime number between n3 and (n + 1)3 if n is sufficiently large. Note however that not even the Lindelöf hypothesis, which assumes that we can take c to be any positive number, implies that there is a prime number between n2 and (n + 1)2, if n is sufficiently large (see Legendre's conjecture
Legendre's conjecture
Legendre's conjecture, proposed by Adrien-Marie Legendre, states that there is a prime number between n2 and 2 for every positive integer n. The conjecture is one of Landau's problems and unproven ....
). To verify this, a stronger result such as Cramér's conjecture would be needed.
Huxley
Martin Huxley
Martin Neil Huxley is a British mathematician, working in the field of analytic number theory.He was awarded a PhD from the University of Cambridge in 1970, the year after his supervisor Harold Davenport had died...
showed that one may choose θ = 7/12.
A recent result, due to Baker, Harman
Glyn Harman
Glyn Harman is a British mathematician working in analytic number theory. One of his major interests is prime number theory. He is best known for results on gaps between primes and the greatest prime factor of p + a, as well as his lower bound for the number of Carmichael numbers up to X...
and Pintz
János Pintz
János Pintz is a Hungarian mathematician working in analytic number theory. He is a fellow of the Rényi Mathematical Institute and is also a member of the Hungarian Academy of Sciences.-Mathematical results:...
, shows that θ may be taken to be 0.525.
In 2005, Daniel Goldston
Daniel Goldston
Daniel Alan Goldston is an American mathematician who specializes in number theory. He is currently a professor of mathematics at San Jose State University....
, János Pintz
János Pintz
János Pintz is a Hungarian mathematician working in analytic number theory. He is a fellow of the Rényi Mathematical Institute and is also a member of the Hungarian Academy of Sciences.-Mathematical results:...
and Cem Yıldırım
Cem Yildirim
Cem Yalçın Yıldırım is a Turkish mathematician who specializes in number theory. He obtained his PhD from the University of Toronto in 1990. His advisor was John Friedlander...
have proved that
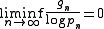
Lower bounds
Robert RankinRobert Alexander Rankin
Robert Alexander Rankin was a Scottish mathematician who worked in analytic number theory.Rankin's father, the Revd Oliver Shaw Rankin, was a minister who later became Professor of Old Testament Language, Literature and Theology in the University of Edinburgh.Rankin was born in Garlieston,...
proved the existence of a constant c > 0 such that the inequality
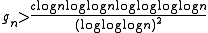
holds for infinitely many values n. The best known value of the constant c is currently c = 2eγ, where γ is the Euler–Mascheroni constant. Paul Erdős
Paul Erdos
Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
offered a $5,000 prize for a proof or disproof that the constant c in the above inequality may be taken arbitrarily large.
Conjectures about gaps between primes
Even better results are possible if it is assumed that the Riemann hypothesisRiemann hypothesis
In mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
is true. Harald Cramér
Harald Cramér
Harald Cramér was a Swedish mathematician, actuary, and statistician, specializing in mathematical statistics and probabilistic number theory. He was once described by John Kingman as "one of the giants of statistical theory".-Early life:Harald Cramér was born in Stockholm, Sweden on September...
proved that, under this assumption, the gap g(pn) satisfies
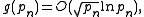
using the big O notation
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
.
Later, he conjectured that the gaps are even smaller. Roughly speaking he conjectured that
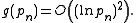
At the moment, the numerical evidence seems to point in this direction. See Cramér's conjecture for more details.
Andrica's conjecture states that
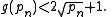
This is a slight strengthening of Legendre's conjecture
Legendre's conjecture
Legendre's conjecture, proposed by Adrien-Marie Legendre, states that there is a prime number between n2 and 2 for every positive integer n. The conjecture is one of Landau's problems and unproven ....
that between successive square numbers there is always a prime.
As an arithmetic function
The gap gn between the nth and (n + 1)st prime numbers is an example of an arithmetic functionArithmetic function
In number theory, an arithmetic function is a real or complex valued function ƒ defined on the set of natural numbers In number theory, an arithmetic (or arithmetical) function is a real or complex valued function ƒ(n) defined on the set of natural numbers In number theory, an arithmetic (or...
. In this context it is usually denoted dn and called the prime difference function. The function is neither multiplicative
Multiplicative function
In number theory, a multiplicative function is an arithmetic function f of the positive integer n with the property that f = 1 and whenevera and b are coprime, then...
nor additive
Additive function
In mathematics the term additive function has two different definitions, depending on the specific field of application.In algebra an additive function is a function that preserves the addition operation:for any two elements x and y in the domain. For example, any linear map is additive...
.
External links
- Thomas R. Nicely, Some Results of Computational Research in Prime Numbers -- Computational Number Theory. This reference web site includes a list of all first known occurrence prime gaps.
- Chris Caldwell, Gaps Between Primes