Mertens function
Encyclopedia
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, the Mertens function is defined for all positive integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s n as
where μ(k) is the Möbius function
Möbius function
The classical Möbius function μ is an important multiplicative function in number theory and combinatorics. The German mathematician August Ferdinand Möbius introduced it in 1832...
. The function is named in honour of Franz Mertens
Franz Mertens
Franz Mertens was a German mathematician. He was born in Środa in the Grand Duchy of Poznań, Kingdom of Prussia and died in Vienna, Austria....
.
Less formally, M(n) is the count of square-free integer
Square-free integer
In mathematics, a square-free, or quadratfrei, integer is one divisible by no perfect square, except 1. For example, 10 is square-free but 18 is not, as it is divisible by 9 = 32...
s up to n that have an even number of prime factors, minus the count of those that have an odd number. The
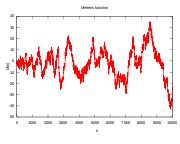
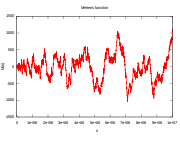
Mertens function slowly grows in positive and negative directions both on average and in peak value, oscillating in an apparently chaotic manner passing through zero when n has the values
- 2, 39, 40, 58, 65, 93, 101, 145, 149, 150, 159, 160, 163, 164, 166, 214, 231, 232, 235, 236, 238, 254, ... .
Because the Möbius function only takes the values −1, 0, and +1, the Mertens function moves slowly and there is no n such that |M(n)| > n. The Mertens conjecture
Mertens conjecture
In mathematics, the Mertens conjecture is the incorrect statement that the Mertens function M is bounded by √n, which implies the Riemann hypothesis...
went further, stating that there would be no n where the absolute value of the Mertens function exceeds the square root of n. The Mertens conjecture was proven false in 1985 by Andrew Odlyzko
Andrew Odlyzko
Andrew Michael Odlyzko is a mathematician and a former head of the University of Minnesota's Digital Technology Center.In the field of mathematics he has published extensively on analytic number theory, computational number theory, cryptography, algorithms and computational complexity,...
and Herman te Riele. However, the Riemann hypothesis
Riemann hypothesis
In mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
is equivalent to a weaker conjecture on the growth of M(n), namely M(n) = O(n1/2 + ε). Since high values for M(n) grow at least as fast as the square root of n, this puts a rather tight bound on its rate of growth. Here, O refers to Big O notation
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
.
The above definition can be extended to real numbers as follows:
As an integral
Using the Euler productEuler product
In number theory, an Euler product is an expansion of a Dirichlet series into an infinite product indexed by prime numbers. The name arose from the case of the Riemann zeta-function, where such a product representation was proved by Leonhard Euler.-Definition:...
one finds that
where
is the Riemann zeta function and the product is taken over primes. Then, using this Dirichlet series with Perron's formulaPerron's formula
In mathematics, and more particularly in analytic number theory, Perron's formula is a formula due to Oskar Perron to calculate the sum of an arithmetical function, by means of an inverse Mellin transform.-Statement:...
, one obtains:
where C is a closed curve encircling all of the roots of
Conversely, one has the Mellin transform
Mellin transform
In mathematics, the Mellin transform is an integral transform that may be regarded as the multiplicative version of the two-sided Laplace transform...
which holds for
.A curious relation given by Mertens himself involving the second Chebyshev function
Chebyshev function
[Image:ChebyshevPsi.png|thumb|right|The Chebyshev function ψ, with x [Image:ChebyshevPsi.png|thumb|right|The Chebyshev function ψ, with x ...
is
A good evaluation, at least asymptotically, would be to obtain, by the method of steepest descent, the inequality
Assuming that there are not multiple non-trivial roots of
we have the "exact formula" by the residue theoremResidue theorem
The residue theorem, sometimes called Cauchy's Residue Theorem, in complex analysis is a powerful tool to evaluate line integrals of analytic functions over closed curves and can often be used to compute real integrals as well. It generalizes the Cauchy integral theorem and Cauchy's integral formula...
:
Weyl conjectured that the Mertens function satisfied the approximate functional-differential equation
where H(x) is the Heaviside step function
Heaviside step function
The Heaviside step function, or the unit step function, usually denoted by H , is a discontinuous function whose value is zero for negative argument and one for positive argument....
, B are Bernoulli number
Bernoulli number
In mathematics, the Bernoulli numbers Bn are a sequence of rational numbers with deep connections to number theory. They are closely related to the values of the Riemann zeta function at negative integers....
s and all derivatives with respect to t are evaluated at t = 0.
Titchmarsh
Edward Charles Titchmarsh
Edward Charles "Ted" Titchmarsh was a leading British mathematician.He was educated at King Edward VII School and Balliol College, Oxford, where he began his studies in October 1917....
(1960) provided a Trace formula involving a sum over the Möbius function and zeros of Riemann Zeta in the form
where 't' sums over the imaginary parts of nontrivial zeros, and (g, h) are related by a Fourier transform, such that
As a sum over Farey sequences
Another formula for the Mertens function is
where 
is the Farey sequenceFarey sequence
In mathematics, the Farey sequence of order n is the sequence of completely reduced fractions between 0 and 1 which, when in lowest terms, have denominators less than or equal to n, arranged in order of increasing size....
of order n.
This formula is used in the proof of the Franel–Landau theorem.
As a determinant
M(n) is the determinantDeterminant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the n × n Redheffer matrix
Redheffer matrix
In mathematics, a Redheffer matrix, studied by , is a matrix whose entries aij are 1 if i divides j or if j = 1; otherwise, aij = 0....
, a (0,1) matrix in which
aij is 1 if either j is 1 or i divides j.
Calculation
The Mertens function has been computed for an increasing range of n.| Person | Year | Limit |
| Mertens | 1897 | 104 |
| von Sterneck | 1897 | 1.5 |
| von Sterneck | 1901 | 5 |
| von Sterneck | 1912 | 5 |
| Neubauer | 1963 | 108 |
| Cohen and Dress | 1979 | 7.8 |
| Dress | 1993 | 1012 |
| Lioen and van de Lune | 1994 | 1013 |
| Kotnik and van de Lune | 2003 | 1014 |