
Selberg zeta function
Encyclopedia
The Selberg zeta-function was introduced by . It is analogous to the famous Riemann zeta function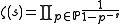
where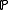 is the set of prime numbers. The Selberg zeta-function uses the lengths of simple closed geodesic
is the set of prime numbers. The Selberg zeta-function uses the lengths of simple closed geodesic
s instead of the primes numbers.
For any hyperbolic surface
of finite area there is an associated Selberg zeta-function; this function is a meromorphic function
defined in the complex plane
. The zeta function is defined in terms of the closed geodesic
s of the surface.
The zeros and poles of the Selberg zeta-function, Z(s), can be described in terms of spectral data of the surface.
The zeros are at the following points:
The zeta-function also has poles at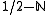 , and can have zeros or poles at the points
, and can have zeros or poles at the points 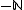 .
.
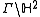 , where
, where 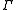 is the modular group
is the modular group
, the Selberg zeta-function is of special interest. For this special case the Selberg zeta-function is intimately connected to the Riemann zeta-function.
In this case the scattering matrix is given by: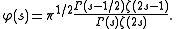
In particular, we see that if the Riemann zeta-function has a zero at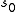 , then the scattering matrix has a pole at
, then the scattering matrix has a pole at 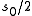 , and hence the Selberg zeta-function has a zero at
, and hence the Selberg zeta-function has a zero at 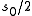 .
.
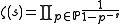
where
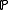 is the set of prime numbers. The Selberg zeta-function uses the lengths of simple closed geodesic
is the set of prime numbers. The Selberg zeta-function uses the lengths of simple closed geodesicClosed geodesic
In differential geometry and dynamical systems, a closed geodesic on a Riemannian manifold M is the projection of a closed orbit of the geodesic flow on M.-Examples:On the unit sphere, every great circle is an example of a closed geodesic...
s instead of the primes numbers.
For any hyperbolic surface
Hyperbolic manifold
In mathematics, a hyperbolic n-manifold is a complete Riemannian n-manifold of constant sectional curvature -1.Every complete, connected, simply-connected manifold of constant negative curvature −1 is isometric to the real hyperbolic space Hn. As a result, the universal cover of any closed manifold...
of finite area there is an associated Selberg zeta-function; this function is a meromorphic function
Meromorphic function
In complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...
defined in the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
. The zeta function is defined in terms of the closed geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
s of the surface.
The zeros and poles of the Selberg zeta-function, Z(s), can be described in terms of spectral data of the surface.
The zeros are at the following points:
- For every cusp form with eigenvalue
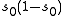 there exists a zero at the point
there exists a zero at the point 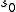 . The order of the zero equals the dimension of the corresponding eigenspace. (A cusp form is an eigenfunction to the Laplace-Beltrami operatorLaplace-Beltrami operatorIn differential geometry, the Laplace operator, named after Pierre-Simon Laplace, can be generalized to operate on functions defined on surfaces in Euclidean space and, more generally, on Riemannian and pseudo-Riemannian manifolds. This more general operator goes by the name Laplace–Beltrami...
. The order of the zero equals the dimension of the corresponding eigenspace. (A cusp form is an eigenfunction to the Laplace-Beltrami operatorLaplace-Beltrami operatorIn differential geometry, the Laplace operator, named after Pierre-Simon Laplace, can be generalized to operate on functions defined on surfaces in Euclidean space and, more generally, on Riemannian and pseudo-Riemannian manifolds. This more general operator goes by the name Laplace–Beltrami...
which has Fourier expansion with zero constant term.) - The zeta-function also has a zero at every pole of the determinant of the scattering matrix,
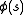 . The order of the zero equals the order of the corresponding pole of the scattering matrix.
. The order of the zero equals the order of the corresponding pole of the scattering matrix.
The zeta-function also has poles at
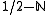 , and can have zeros or poles at the points
, and can have zeros or poles at the points 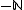 .
.Selberg zeta-function for the modular group
For the case where the surface is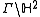 , where
, where 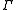 is the modular group
is the modular groupModular group
In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
, the Selberg zeta-function is of special interest. For this special case the Selberg zeta-function is intimately connected to the Riemann zeta-function.
In this case the scattering matrix is given by:
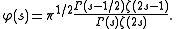
In particular, we see that if the Riemann zeta-function has a zero at
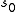 , then the scattering matrix has a pole at
, then the scattering matrix has a pole at 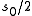 , and hence the Selberg zeta-function has a zero at
, and hence the Selberg zeta-function has a zero at 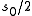 .
.

