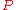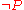Vacuous truth
Encyclopedia
A vacuous truth is a truth
that is devoid of content because it asserts something about all members of a class that is empty or because it says "If A then B" when in fact A is inherently false. For example, the statement "all cell phones in the room are turned off" may be true simply because there are no cell phones in the room. In this case, the statement "all cell phones in the room are turned on" would also be considered true, and vacuously so, as would the conjunction of the two: "all cell phones in the room are turned on and turned off".
More formally, a relatively well-defined usage refers to a conditional
statement with a false antecedent
. One example of such a statement is "if Uluru
is in France, then the Eiffel tower
is in Bolivia". Such statements are considered vacuous because the falsity of the antecedent prevents one from using the conditional to infer the consequent. They are true because a material conditional
is defined to be true when the antecedent is false (or the conclusion is true).
This notion has relevance in pure mathematics
, as well as in any other field which uses classical logic
.
Outside of mathematics, statements which can be characterized informally as vacuously true can be misleading. Such statements make reasonable assertions about qualified objects which do not actually exist. For example, a child might tell his parents "I ate every vegetable on my plate," when there were no vegetables on the child’s plate to begin with.
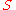 is "vacuously true" if it resembles the statement
is "vacuously true" if it resembles the statement  and
and 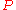 is false.
is false.
Statements that can be reduced (with suitable transformations) to this basic form include the following:
Vacuous truth is usually applied in classical logic
, which in particular is two-valued, and most of the arguments in the next section will be based on this assumption.
However, vacuous truth also appears in, for example, intuitionistic logic
in the same situations given above.
Indeed, the first 2 forms above will yield vacuous truth in any logic that uses material conditional
, but there are other logics which do not.
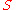 has the form
has the form  , and
, and 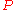 is false. This case strikes many people as odd, and it’s not immediately obvious whether all such statements are true, all such statements are false, or some are true while others are false.
is false. This case strikes many people as odd, and it’s not immediately obvious whether all such statements are true, all such statements are false, or some are true while others are false.
Second, the most obvious alternative to taking all vacuously true statements to be true — that is, taking all vacuously true statements to be false — has some unsavory consequences. Suppose we are willing to accept that should be true when both
should be true when both 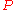 and
and  are true, and false when
are true, and false when 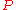 is true but
is true but  is false. That is, suppose we accept this as a partial truth table
is false. That is, suppose we accept this as a partial truth table
for implies:
Suppose we decide that the unknown values should be . In this case, then implies turns out to be logically equivalent
. In this case, then implies turns out to be logically equivalent
to logical AND ( ), as we can see in the following table:
), as we can see in the following table:
Intuitively this is odd, because it certainly seems like "if" and "and" ought to have different meanings; if they didn’t, then it’s confusing why we should have a separate logical symbol for each one.
Perhaps more disturbing, we must also accept that the following arguments are logically valid:
and
That is, we can conclude that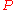 is true (or that
is true (or that  is true) based solely on the logical connection of the two.
is true) based solely on the logical connection of the two.
Making vacuous implications "true" makes many mathematical propositions that people tend to think are true come out as true. For example, most people would say that the statement
is true. Now suppose that we decide to say that all vacuously true statements are false. In that case, the vacuously true statement
is false. But in this case, there is an integer value for (namely,
(namely,  ), for which it does not hold that
), for which it does not hold that
Therefore our first statement isn’t true, as we said before, but false. This does not seem to be how people intuitively use language, however.
First, calling vacuously true sentences false may extend the term "lying" to too many different situations. Note that lying could be defined as knowingly making a false statement. Now suppose two male friends, Peter and Ned, read this very article on some June 4, and both (perhaps unwisely) concluded that "vacuously true" sentences, despite their name, are actually false. Suppose the same day, Peter tells Ned the following statement :
:
Suppose June 5 goes by without Ned getting his new house. Now according to Peter and Ned’s common understanding that vacuous sentences are false, is a false statement. Moreover, since Peter knew that he was not female when he uttered
is a false statement. Moreover, since Peter knew that he was not female when he uttered 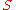 , we can assume he knew, at that time, that
, we can assume he knew, at that time, that 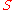 was vacuous, and hence false. Since Peter has spoken a falsehood, then Ned has every right to accuse Peter of having lied to him. On the face of it, this line of reasoning appears to be suspect.
was vacuous, and hence false. Since Peter has spoken a falsehood, then Ned has every right to accuse Peter of having lied to him. On the face of it, this line of reasoning appears to be suspect.
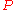 is false, then
is false, then  is true. That is, if we accept those axioms, we must accept that vacuously true statements are indeed true. For many people, the axioms of propositional logic are obviously truth-preserving. These people, then, really ought to accept that vacuously true statements are indeed true. On the other hand, if one is willing to question whether all vacuously true statements are indeed true, one may also be quite willing to question the validity of the propositional calculus, in which case this argument begs the question.
is true. That is, if we accept those axioms, we must accept that vacuously true statements are indeed true. For many people, the axioms of propositional logic are obviously truth-preserving. These people, then, really ought to accept that vacuously true statements are indeed true. On the other hand, if one is willing to question whether all vacuously true statements are indeed true, one may also be quite willing to question the validity of the propositional calculus, in which case this argument begs the question.
Many people have trouble with or are bothered by this because, unless we know about some a priori
connection between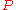 and
and  , what should the truth of
, what should the truth of 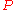 have to do with the implication of
have to do with the implication of 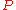 and
and  ? Shouldn’t the truth value of
? Shouldn’t the truth value of  in this situation be irrelevant? Logicians bothered by this have developed alternative logics (e.g. relevant logic) where this sort of deduction is valid only when
in this situation be irrelevant? Logicians bothered by this have developed alternative logics (e.g. relevant logic) where this sort of deduction is valid only when 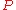 is known a priori to be relevant to the truth of
is known a priori to be relevant to the truth of  .
.
Note that this "relevance" objection really applies to logical implication as a whole, and not merely to the case of vacuous truth. For example, it’s commonly accepted that the sun is made of gas, on one hand, and that 3 is a prime number, on the other. By the standard definition of implication, we can conclude that: the sun’s being made of gas implies that 3 is a prime number. Note that since the premise is indeed true, this is not a case of vacuous truth. Nonetheless, there seems to be something fishy about this assertion.
Nonetheless, there is still something odd about the choice.
There seems to be no direct reason to pick true; it’s just that things blow up in our face if we don’t.
Thus we say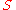 is vacuously true; it is true, but in a way that doesn’t seem entirely free from arbitrariness.
is vacuously true; it is true, but in a way that doesn’t seem entirely free from arbitrariness.
Furthermore, the fact that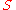 is true doesn’t really provide us with any information, nor can we make useful deductions from it; it is only a choice we made about how our logical system works, and can’t represent any fact of the real
is true doesn’t really provide us with any information, nor can we make useful deductions from it; it is only a choice we made about how our logical system works, and can’t represent any fact of the real
world.
Both of these seemingly contradictory statements are true using classical or two-valued logic – so long as the set of pink rhinoceros remains empty. (See also Present King of France.)
One fundamental problem with such ‘demonstrations’ is the uncertainty of the truth-value of any of the statements which follow (or even whether they do follow) when our initial supposition is false. Stated another way, we should ask ourselves which rules of mathematics or inference should still be applicable if we suppose that pi is an integer (which it is not).
The problem occurs when it is not immediately obvious that we are dealing with a vacuous truth. For example, if we have two propositions, neither of which implies the other, then we can reasonably conclude that they are different; counter-intuitively, we can also conclude that the two propositions are the same. The reason for this is that is a tautology
is a tautology
in classical logic, so every assertion that is made about "two propositions, neither of which implies the other" is an assertion about nothing, hence vacuously true. Although such a fact that "two propositions, neither of which implies the other, are both different and the same" poses no theoretical problems, it can easily be disturbing to the human mind.
Avoidance of such paradox is the impetus behind the development of non-classical systems of logic relevant logic and paraconsistent logic
which refuse to admit the validity of one or two of the axiom
s of classical logic
. Unfortunately the resulting systems are often too weak to prove anything but the most trivial of truths.
. For instance, when making a general statement about arbitrary sets, said statement ought to hold for all sets including the empty set
. But for the empty set the statement may very well reduce to a vacuous truth. So by taking this vacuous truth to be true, our general statement stands and we are not forced to make an exception for the empty set.
For example, consider the property of being an antisymmetric relation
. A relation on a set
on a set 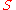 is antisymmetric if, for any
is antisymmetric if, for any  and
and  in
in 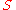 with
with  and
and  , it is true that
, it is true that  . The less-than-or-equal-to relation
. The less-than-or-equal-to relation  on the real numbers is an example of an antisymmetric relation, because whenever
on the real numbers is an example of an antisymmetric relation, because whenever  and
and  , it is true that
, it is true that  . The less-than relation
. The less-than relation  is also antisymmetric, and vacuously so, because there are no numbers
is also antisymmetric, and vacuously so, because there are no numbers  and
and  for which both
for which both  and
and  , and so the conclusion, that
, and so the conclusion, that  whenever this occurs, is vacuously true.
whenever this occurs, is vacuously true.
An even simpler example concerns the theorem that says that for any set , the empty set
, the empty set  is a subset of
is a subset of  . This is equivalent to asserting that every element of
. This is equivalent to asserting that every element of  is an element of
is an element of  , which is vacuously true since there are no elements of
, which is vacuously true since there are no elements of  .
.
There are however vacuous truths that even most mathematicians will outright dismiss as "nonsense
" and would never publish in a mathematical journal (even if grudgingly admitting that they are true). An example would be the true statement
More disturbing are generalizations of obviously "nonsensical" statements which are likewise true, but not vacuously so:
Since no infinite subset of any set has precisely seven elements, we may be tempted to conclude that this statement is obviously false. But this is wrong, because we’ve failed to consider the possibility of sets that have no infinite subsets at all (as in the previous example—in fact, any finite set will do). It is this sort of "hidden" vacuous truth that can easily invalidate a proof when not treated with care.
Truth
Truth has a variety of meanings, such as the state of being in accord with fact or reality. It can also mean having fidelity to an original or to a standard or ideal. In a common usage, it also means constancy or sincerity in action or character...
that is devoid of content because it asserts something about all members of a class that is empty or because it says "If A then B" when in fact A is inherently false. For example, the statement "all cell phones in the room are turned off" may be true simply because there are no cell phones in the room. In this case, the statement "all cell phones in the room are turned on" would also be considered true, and vacuously so, as would the conjunction of the two: "all cell phones in the room are turned on and turned off".
More formally, a relatively well-defined usage refers to a conditional
Counterfactual conditional
A counterfactual conditional, subjunctive conditional, or remote conditional, abbreviated , is a conditional statement indicating what would be the case if its antecedent were true...
statement with a false antecedent
Antecedent (logic)
An antecedent is the first half of a hypothetical proposition.Examples:* If P, then Q.This is a nonlogical formulation of a hypothetical proposition...
. One example of such a statement is "if Uluru
Uluru
Uluru , also known as Ayers Rock, is a large sandstone rock formation in the southern part of the Northern Territory, central Australia. It lies south west of the nearest large town, Alice Springs; by road. Kata Tjuta and Uluru are the two major features of the Uluṟu-Kata Tjuṯa National Park....
is in France, then the Eiffel tower
Eiffel Tower
The Eiffel Tower is a puddle iron lattice tower located on the Champ de Mars in Paris. Built in 1889, it has become both a global icon of France and one of the most recognizable structures in the world...
is in Bolivia". Such statements are considered vacuous because the falsity of the antecedent prevents one from using the conditional to infer the consequent. They are true because a material conditional
Material conditional
The material conditional, also known as material implication, is a binary truth function, such that the compound sentence p→q is logically equivalent to the negative compound: not . A material conditional compound itself is often simply called a conditional...
is defined to be true when the antecedent is false (or the conclusion is true).
This notion has relevance in pure mathematics
Pure mathematics
Broadly speaking, pure mathematics is mathematics which studies entirely abstract concepts. From the eighteenth century onwards, this was a recognized category of mathematical activity, sometimes characterized as speculative mathematics, and at variance with the trend towards meeting the needs of...
, as well as in any other field which uses classical logic
Classical logic
Classical logic identifies a class of formal logics that have been most intensively studied and most widely used. The class is sometimes called standard logic as well...
.
Outside of mathematics, statements which can be characterized informally as vacuously true can be misleading. Such statements make reasonable assertions about qualified objects which do not actually exist. For example, a child might tell his parents "I ate every vegetable on my plate," when there were no vegetables on the child’s plate to begin with.
Scope of the concept
A statement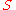 is "vacuously true" if it resembles the statement
is "vacuously true" if it resembles the statement  and
and 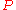 is false.
is false.Statements that can be reduced (with suitable transformations) to this basic form include the following:
-
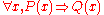 , where it is the case that
, where it is the case that 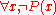 .
. -
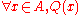 , where the set
, where the set  is emptyEmpty setIn mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
is emptyEmpty setIn mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
. -
 , where the symbol
, where the symbol  is restricted to a type that has no representatives.
is restricted to a type that has no representatives.
Vacuous truth is usually applied in classical logic
Classical logic
Classical logic identifies a class of formal logics that have been most intensively studied and most widely used. The class is sometimes called standard logic as well...
, which in particular is two-valued, and most of the arguments in the next section will be based on this assumption.
However, vacuous truth also appears in, for example, intuitionistic logic
Intuitionistic logic
Intuitionistic logic, or constructive logic, is a symbolic logic system differing from classical logic in its definition of the meaning of a statement being true. In classical logic, all well-formed statements are assumed to be either true or false, even if we do not have a proof of either...
in the same situations given above.
Indeed, the first 2 forms above will yield vacuous truth in any logic that uses material conditional
Material conditional
The material conditional, also known as material implication, is a binary truth function, such that the compound sentence p→q is logically equivalent to the negative compound: not . A material conditional compound itself is often simply called a conditional...
, but there are other logics which do not.
Arguments regarding the semantic truth of vacuously true logical statements
This is a complex question and, for simplicity of exposition, we will here consider only vacuous truth as concerns logical implication, i.e., the case when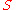 has the form
has the form  , and
, and 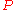 is false. This case strikes many people as odd, and it’s not immediately obvious whether all such statements are true, all such statements are false, or some are true while others are false.
is false. This case strikes many people as odd, and it’s not immediately obvious whether all such statements are true, all such statements are false, or some are true while others are false.Arguments that at least some vacuously true statements are true
Consider the implication "if I am in Massachusetts, then I am in North America", which we might alternatively express as, "if I were in Massachusetts, then I would be in North America". There is something inherently reasonable about this claim, even if one is not currently in Massachusetts. It seems that someone in Europe, for example, would still have good reason to assert this proposition. Thus at least one vacuously true statement seems to actually be true.Causing the Implies Operator and the Logical AND Operator to be logically equivalent
Second, the most obvious alternative to taking all vacuously true statements to be true — that is, taking all vacuously true statements to be false — has some unsavory consequences. Suppose we are willing to accept that
 should be true when both
should be true when both 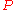 and
and  are true, and false when
are true, and false when 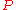 is true but
is true but  is false. That is, suppose we accept this as a partial truth table
is false. That is, suppose we accept this as a partial truth tableTruth table
A truth table is a mathematical table used in logic—specifically in connection with Boolean algebra, boolean functions, and propositional calculus—to compute the functional values of logical expressions on each of their functional arguments, that is, on each combination of values taken by their...
for implies:
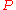 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
? |
 |
 |
? |
Suppose we decide that the unknown values should be
 . In this case, then implies turns out to be logically equivalent
. In this case, then implies turns out to be logically equivalentLogical equivalence
In logic, statements p and q are logically equivalent if they have the same logical content.Syntactically, p and q are equivalent if each can be proved from the other...
to logical AND (
 ), as we can see in the following table:
), as we can see in the following table:  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Intuitively this is odd, because it certainly seems like "if" and "and" ought to have different meanings; if they didn’t, then it’s confusing why we should have a separate logical symbol for each one.
Perhaps more disturbing, we must also accept that the following arguments are logically valid:
and
That is, we can conclude that
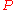 is true (or that
is true (or that  is true) based solely on the logical connection of the two.
is true) based solely on the logical connection of the two.Intuition from mathematical arguments
Making vacuous implications "true" makes many mathematical propositions that people tend to think are true come out as true. For example, most people would say that the statement
- For all integers
 , if
, if  is even, then
is even, then  is even.
is even.
is true. Now suppose that we decide to say that all vacuously true statements are false. In that case, the vacuously true statement
- If 3 is even, then 3 + 2 is even
is false. But in this case, there is an integer value for
 (namely,
(namely,  ), for which it does not hold that
), for which it does not hold that
- if
 is even, then
is even, then  is even
is even
Therefore our first statement isn’t true, as we said before, but false. This does not seem to be how people intuitively use language, however.
A linguistic argument
First, calling vacuously true sentences false may extend the term "lying" to too many different situations. Note that lying could be defined as knowingly making a false statement. Now suppose two male friends, Peter and Ned, read this very article on some June 4, and both (perhaps unwisely) concluded that "vacuously true" sentences, despite their name, are actually false. Suppose the same day, Peter tells Ned the following statement
 :
:
- If I am female today, i.e., June 4, then I will buy you a new house tomorrow, i.e., June 5.
Suppose June 5 goes by without Ned getting his new house. Now according to Peter and Ned’s common understanding that vacuous sentences are false,
 is a false statement. Moreover, since Peter knew that he was not female when he uttered
is a false statement. Moreover, since Peter knew that he was not female when he uttered 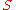 , we can assume he knew, at that time, that
, we can assume he knew, at that time, that 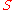 was vacuous, and hence false. Since Peter has spoken a falsehood, then Ned has every right to accuse Peter of having lied to him. On the face of it, this line of reasoning appears to be suspect.
was vacuous, and hence false. Since Peter has spoken a falsehood, then Ned has every right to accuse Peter of having lied to him. On the face of it, this line of reasoning appears to be suspect.Arguments for taking all vacuously true statements to be true
The main argument that all vacuously true statements are true is as follows: As explained in the article on logical conditionals, the axioms of propositional logic entail that if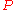 is false, then
is false, then  is true. That is, if we accept those axioms, we must accept that vacuously true statements are indeed true. For many people, the axioms of propositional logic are obviously truth-preserving. These people, then, really ought to accept that vacuously true statements are indeed true. On the other hand, if one is willing to question whether all vacuously true statements are indeed true, one may also be quite willing to question the validity of the propositional calculus, in which case this argument begs the question.
is true. That is, if we accept those axioms, we must accept that vacuously true statements are indeed true. For many people, the axioms of propositional logic are obviously truth-preserving. These people, then, really ought to accept that vacuously true statements are indeed true. On the other hand, if one is willing to question whether all vacuously true statements are indeed true, one may also be quite willing to question the validity of the propositional calculus, in which case this argument begs the question.Arguments that only some vacuously true statements are true
One objection to saying that all vacuously true statements are true is that this makes the following deduction valid:Many people have trouble with or are bothered by this because, unless we know about some a priori
A priori and a posteriori (philosophy)
The terms a priori and a posteriori are used in philosophy to distinguish two types of knowledge, justifications or arguments...
connection between
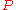 and
and  , what should the truth of
, what should the truth of 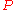 have to do with the implication of
have to do with the implication of 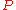 and
and  ? Shouldn’t the truth value of
? Shouldn’t the truth value of  in this situation be irrelevant? Logicians bothered by this have developed alternative logics (e.g. relevant logic) where this sort of deduction is valid only when
in this situation be irrelevant? Logicians bothered by this have developed alternative logics (e.g. relevant logic) where this sort of deduction is valid only when 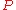 is known a priori to be relevant to the truth of
is known a priori to be relevant to the truth of  .
.Note that this "relevance" objection really applies to logical implication as a whole, and not merely to the case of vacuous truth. For example, it’s commonly accepted that the sun is made of gas, on one hand, and that 3 is a prime number, on the other. By the standard definition of implication, we can conclude that: the sun’s being made of gas implies that 3 is a prime number. Note that since the premise is indeed true, this is not a case of vacuous truth. Nonetheless, there seems to be something fishy about this assertion.
Summary
So there are a number of justifications for saying that vacuously true statements are indeed true.Nonetheless, there is still something odd about the choice.
There seems to be no direct reason to pick true; it’s just that things blow up in our face if we don’t.
Thus we say
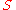 is vacuously true; it is true, but in a way that doesn’t seem entirely free from arbitrariness.
is vacuously true; it is true, but in a way that doesn’t seem entirely free from arbitrariness.Furthermore, the fact that
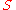 is true doesn’t really provide us with any information, nor can we make useful deductions from it; it is only a choice we made about how our logical system works, and can’t represent any fact of the real
is true doesn’t really provide us with any information, nor can we make useful deductions from it; it is only a choice we made about how our logical system works, and can’t represent any fact of the realworld.
Difficulties with the use of vacuous truth
- All pink rhinoceros are carnivores.
- All pink rhinoceros are herbivores.
Both of these seemingly contradictory statements are true using classical or two-valued logic – so long as the set of pink rhinoceros remains empty. (See also Present King of France.)
One fundamental problem with such ‘demonstrations’ is the uncertainty of the truth-value of any of the statements which follow (or even whether they do follow) when our initial supposition is false. Stated another way, we should ask ourselves which rules of mathematics or inference should still be applicable if we suppose that pi is an integer (which it is not).
The problem occurs when it is not immediately obvious that we are dealing with a vacuous truth. For example, if we have two propositions, neither of which implies the other, then we can reasonably conclude that they are different; counter-intuitively, we can also conclude that the two propositions are the same. The reason for this is that
 is a tautology
is a tautologyTautology (logic)
In logic, a tautology is a formula which is true in every possible interpretation. Philosopher Ludwig Wittgenstein first applied the term to redundancies of propositional logic in 1921; it had been used earlier to refer to rhetorical tautologies, and continues to be used in that alternate sense...
in classical logic, so every assertion that is made about "two propositions, neither of which implies the other" is an assertion about nothing, hence vacuously true. Although such a fact that "two propositions, neither of which implies the other, are both different and the same" poses no theoretical problems, it can easily be disturbing to the human mind.
Avoidance of such paradox is the impetus behind the development of non-classical systems of logic relevant logic and paraconsistent logic
Paraconsistent logic
A paraconsistent logic is a logical system that attempts to deal with contradictions in a discriminating way. Alternatively, paraconsistent logic is the subfield of logic that is concerned with studying and developing paraconsistent systems of logic.Inconsistency-tolerant logics have been...
which refuse to admit the validity of one or two of the axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s of classical logic
Classical logic
Classical logic identifies a class of formal logics that have been most intensively studied and most widely used. The class is sometimes called standard logic as well...
. Unfortunately the resulting systems are often too weak to prove anything but the most trivial of truths.
Vacuous truths in mathematics
Vacuous truths occur commonly in mathematicsMathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
. For instance, when making a general statement about arbitrary sets, said statement ought to hold for all sets including the empty set
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
. But for the empty set the statement may very well reduce to a vacuous truth. So by taking this vacuous truth to be true, our general statement stands and we are not forced to make an exception for the empty set.
For example, consider the property of being an antisymmetric relation
Antisymmetric relation
In mathematics, a binary relation R on a set X is antisymmetric if, for all a and b in Xor, equivalently,In mathematical notation, this is:\forall a, b \in X,\ R \and R \; \Rightarrow \; a = bor, equivalently,...
. A relation
 on a set
on a set 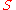 is antisymmetric if, for any
is antisymmetric if, for any  and
and  in
in 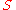 with
with  and
and  , it is true that
, it is true that  . The less-than-or-equal-to relation
. The less-than-or-equal-to relation  on the real numbers is an example of an antisymmetric relation, because whenever
on the real numbers is an example of an antisymmetric relation, because whenever  and
and  , it is true that
, it is true that  . The less-than relation
. The less-than relation  is also antisymmetric, and vacuously so, because there are no numbers
is also antisymmetric, and vacuously so, because there are no numbers  and
and  for which both
for which both  and
and  , and so the conclusion, that
, and so the conclusion, that  whenever this occurs, is vacuously true.
whenever this occurs, is vacuously true.An even simpler example concerns the theorem that says that for any set
 , the empty set
, the empty set  is a subset of
is a subset of  . This is equivalent to asserting that every element of
. This is equivalent to asserting that every element of  is an element of
is an element of  , which is vacuously true since there are no elements of
, which is vacuously true since there are no elements of  .
.There are however vacuous truths that even most mathematicians will outright dismiss as "nonsense
Nonsense
Nonsense is a communication, via speech, writing, or any other symbolic system, that lacks any coherent meaning. Sometimes in ordinary usage, nonsense is synonymous with absurdity or the ridiculous...
" and would never publish in a mathematical journal (even if grudgingly admitting that they are true). An example would be the true statement
- Every infinite subsetSubsetIn mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of the set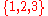 has precisely seven elements.
has precisely seven elements.
More disturbing are generalizations of obviously "nonsensical" statements which are likewise true, but not vacuously so:
- There exists a set S such that every infinite subset of S has precisely seven elements.
Since no infinite subset of any set has precisely seven elements, we may be tempted to conclude that this statement is obviously false. But this is wrong, because we’ve failed to consider the possibility of sets that have no infinite subsets at all (as in the previous example—in fact, any finite set will do). It is this sort of "hidden" vacuous truth that can easily invalidate a proof when not treated with care.
See also
- Counterfactual conditionalCounterfactual conditionalA counterfactual conditional, subjunctive conditional, or remote conditional, abbreviated , is a conditional statement indicating what would be the case if its antecedent were true...
- Degeneracy (mathematics)Degeneracy (mathematics)In mathematics, a degenerate case is a limiting case in which a class of object changes its nature so as to belong to another, usually simpler, class....
- Tautology (logic)Tautology (logic)In logic, a tautology is a formula which is true in every possible interpretation. Philosopher Ludwig Wittgenstein first applied the term to redundancies of propositional logic in 1921; it had been used earlier to refer to rhetorical tautologies, and continues to be used in that alternate sense...
- Trivial (mathematics)Trivial (mathematics)In mathematics, the adjective trivial is frequently used for objects that have a very simple structure...