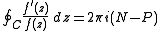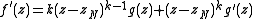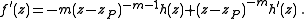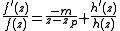Argument principle
Encyclopedia
In complex analysis
, the argument principle (or Cauchy's argument principle) determines the difference between the number of zeros
and poles of a meromorphic function
by computing a contour integral of the function's logarithmic derivative
.
Specifically, if f(z) is a meromorphic function inside and on some closed contour C, with f having no zeros
or poles on C, then
where N and P denote respectively the number of zeros and poles of f(z) inside the contour C, with each zero and pole counted as many times as its multiplicity
and order respectively. This statement of the theorem assumes that the contour C is simple, that is, without self-intersections, and that it is oriented counter-clockwise.
More generally, suppose that f(z) is a meromorphic function on an open set
Ω in the complex plane
and that C is a closed curve in Ω which avoids all zeros and poles of f and is contractible to a point inside Ω. For each point z ∈ Ω, let n(C,z) be the winding number
of C around z. Then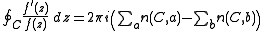
where the first summation is over all zeros a of f counted with their multiplicities, and the second summation is over the poles b of f.
The contour integral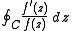 can be interpreted in two ways:
can be interpreted in two ways:
and
Since g(zN) ≠ 0, it follows that g' (z)/g(z) has no singularities at zN, and thus is analytic at zN, which implies that the residue
of f′(z)/f(z) at zN is k.
Let zP be a pole of f. We can write f(z) = (z − zP)−mh(z) where m is the order of the pole, and thus
h(zP) ≠ 0. Then,
and
similarly as above. It follows that h′(z)/h(z) has no singularities at zP since h(zP) ≠ 0 and thus it is analytic at zP. We find that the residue of
f′(z)/f(z) at zP is −m.
Putting these together, each zero zN of multiplicity k of f creates a simple pole for
f′(z)/f(z) with the residue being k, and each pole zP of order m of
f creates a simple pole for f′(z)/f(z) with the residue being −m. (Here, by a simple pole we
mean a pole of order one.) In addition, it can be shown that f′(z)/f(z) has no other poles,
and so no other residues.
By the residue theorem
we have that the integral about C is the product of 2πi and the sum of the residues. Together, the sum of the k 's for each zero zN is the number of zeros counting multiplicities of the zeros, and likewise for the poles, and so we have our result.
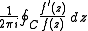 will yield results close to an integer; by determining these integers for different contours C one can obtain information about the location of the zeros and poles. Numerical tests of the Riemann hypothesis
will yield results close to an integer; by determining these integers for different contours C one can obtain information about the location of the zeros and poles. Numerical tests of the Riemann hypothesis
use this technique.
The proof of Rouché's theorem
uses the argument principle.
Modern books on feedback control theory quite frequently use the argument principle to serve as the theoretical basis of the Nyquist stability criterion
.
A consequence of the more general formulation of the argument principle is that, under the same hypothesis, if g is an analytic function in Ω, then
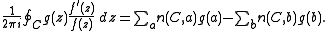
For example, if f is a polynomial
having zeros z1, ..., zp inside a simple contour C, and g(z) = zk, then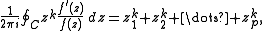
is power sum
symmetric function
of the roots of f.
Another consequence is if we compute the complex integral:
for an appropriate choice of g and f we have the Abel
-Plana
formula:
which expresses the relationship between a discrete sum and its integral.
(Cauchy and the Creation of Complex Function Theory, Cambridge University Press, 1997, p.177), Augustin Louis Cauchy
presented a theorem similar to the above on 27 November 1831, during his self-imposed exile in Turin (capital of the Kingdom of Piedmont-Sardinia in 1831 but now just a city in northern Italy after the unification of Italy) away from France. However, according to this book, only zeroes were mentioned, not poles. This theorem by Cauchy was only published many years later in 1974 in a hand-written form and so is quite difficult to read. Cauchy published a paper with a discussion on both zeroes and poles in 1855, two years before his death.
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, the argument principle (or Cauchy's argument principle) determines the difference between the number of zeros
Zero (complex analysis)
In complex analysis, a zero of a holomorphic function f is a complex number a such that f = 0.-Multiplicity of a zero:A complex number a is a simple zero of f, or a zero of multiplicity 1 of f, if f can be written asf=g\,where g is a holomorphic function g such that g is not zero.Generally, the...
and poles of a meromorphic function
Meromorphic function
In complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...
by computing a contour integral of the function's logarithmic derivative
Logarithmic derivative
In mathematics, specifically in calculus and complex analysis, the logarithmic derivative of a function f is defined by the formulawhere f ′ is the derivative of f....
.
Specifically, if f(z) is a meromorphic function inside and on some closed contour C, with f having no zeros
Zero (complex analysis)
In complex analysis, a zero of a holomorphic function f is a complex number a such that f = 0.-Multiplicity of a zero:A complex number a is a simple zero of f, or a zero of multiplicity 1 of f, if f can be written asf=g\,where g is a holomorphic function g such that g is not zero.Generally, the...
or poles on C, then
where N and P denote respectively the number of zeros and poles of f(z) inside the contour C, with each zero and pole counted as many times as its multiplicity
Multiplicity (mathematics)
In mathematics, the multiplicity of a member of a multiset is the number of times it appears in the multiset. For example, the number of times a given polynomial equation has a root at a given point....
and order respectively. This statement of the theorem assumes that the contour C is simple, that is, without self-intersections, and that it is oriented counter-clockwise.
More generally, suppose that f(z) is a meromorphic function on an open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
Ω in the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
and that C is a closed curve in Ω which avoids all zeros and poles of f and is contractible to a point inside Ω. For each point z ∈ Ω, let n(C,z) be the winding number
Winding number
In mathematics, the winding number of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point...
of C around z. Then
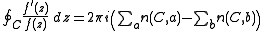
where the first summation is over all zeros a of f counted with their multiplicities, and the second summation is over the poles b of f.
The contour integral
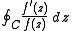 can be interpreted in two ways:
can be interpreted in two ways:
- as the total change in the argument of f(z) as z travels around C (hence the name of the theorem), or
- as 2πi times the winding number of the path foC around the origin.
Proof
Let zN be a zero of f. We can write f(z) = (z − zN)kg(z) where k is the multiplicity of the zero, and thus g(zN) ≠ 0. We getand
Since g(zN) ≠ 0, it follows that g' (z)/g(z) has no singularities at zN, and thus is analytic at zN, which implies that the residue
Residue (complex analysis)
In mathematics, more specifically complex analysis, the residue is a complex number proportional to the contour integral of a meromorphic function along a path enclosing one of its singularities...
of f′(z)/f(z) at zN is k.
Let zP be a pole of f. We can write f(z) = (z − zP)−mh(z) where m is the order of the pole, and thus
h(zP) ≠ 0. Then,
and
similarly as above. It follows that h′(z)/h(z) has no singularities at zP since h(zP) ≠ 0 and thus it is analytic at zP. We find that the residue of
f′(z)/f(z) at zP is −m.
Putting these together, each zero zN of multiplicity k of f creates a simple pole for
f′(z)/f(z) with the residue being k, and each pole zP of order m of
f creates a simple pole for f′(z)/f(z) with the residue being −m. (Here, by a simple pole we
mean a pole of order one.) In addition, it can be shown that f′(z)/f(z) has no other poles,
and so no other residues.
By the residue theorem
Residue theorem
The residue theorem, sometimes called Cauchy's Residue Theorem, in complex analysis is a powerful tool to evaluate line integrals of analytic functions over closed curves and can often be used to compute real integrals as well. It generalizes the Cauchy integral theorem and Cauchy's integral formula...
we have that the integral about C is the product of 2πi and the sum of the residues. Together, the sum of the k 's for each zero zN is the number of zeros counting multiplicities of the zeros, and likewise for the poles, and so we have our result.
Applications and consequences
The argument principle can be used to efficiently locate zeros or poles of meromorphic functions on a computer. Even with rounding errors, the expression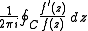 will yield results close to an integer; by determining these integers for different contours C one can obtain information about the location of the zeros and poles. Numerical tests of the Riemann hypothesis
will yield results close to an integer; by determining these integers for different contours C one can obtain information about the location of the zeros and poles. Numerical tests of the Riemann hypothesisRiemann hypothesis
In mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
use this technique.
The proof of Rouché's theorem
Rouché's theorem
Rouché's theorem, named after , states that if the complex-valued functions f and g are holomorphic inside and on some closed contour K, with |g| ...
uses the argument principle.
Modern books on feedback control theory quite frequently use the argument principle to serve as the theoretical basis of the Nyquist stability criterion
Nyquist stability criterion
When designing a feedback control system, it is generally necessary to determine whether the closed-loop system will be stable. An example of a destabilizing feedback control system would be a car steering system that overcompensates -- if the car drifts in one direction, the control system...
.
A consequence of the more general formulation of the argument principle is that, under the same hypothesis, if g is an analytic function in Ω, then
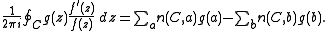
For example, if f is a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
having zeros z1, ..., zp inside a simple contour C, and g(z) = zk, then
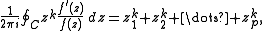
is power sum
Power sum
The topic of power sums is treated at:* Power sum symmetric polynomial * Newton's identities * Symmetric function * Faulhaber's formula...
symmetric function
Symmetric function
In algebra and in particular in algebraic combinatorics, the ring of symmetric functions, is a specific limit of the rings of symmetric polynomials in n indeterminates, as n goes to infinity...
of the roots of f.
Another consequence is if we compute the complex integral:
for an appropriate choice of g and f we have the Abel
Niels Henrik Abel
Niels Henrik Abel was a Norwegian mathematician who proved the impossibility of solving the quintic equation in radicals.-Early life:...
-Plana
Giovanni Antonio Amedeo Plana
Giovanni Antonio Amedeo Plana was an Italian astronomer and mathematician.He was born in Voghera, Italy to Antonio Maria Plana and Giacoboni. At the age of 15 he was sent to live with his uncles in Grenoble to complete his education. In 1800 he entered the École Polytechnique, and was one of the...
formula:
which expresses the relationship between a discrete sum and its integral.
History
According to the book by Frank SmithiesFrank Smithies
Frank Smithies FRSE was a British mathematician who worked on integral equations, functional analysis, and the history of mathematics....
(Cauchy and the Creation of Complex Function Theory, Cambridge University Press, 1997, p.177), Augustin Louis Cauchy
Augustin Louis Cauchy
Baron Augustin-Louis Cauchy was a French mathematician who was an early pioneer of analysis. He started the project of formulating and proving the theorems of infinitesimal calculus in a rigorous manner, rejecting the heuristic principle of the generality of algebra exploited by earlier authors...
presented a theorem similar to the above on 27 November 1831, during his self-imposed exile in Turin (capital of the Kingdom of Piedmont-Sardinia in 1831 but now just a city in northern Italy after the unification of Italy) away from France. However, according to this book, only zeroes were mentioned, not poles. This theorem by Cauchy was only published many years later in 1974 in a hand-written form and so is quite difficult to read. Cauchy published a paper with a discussion on both zeroes and poles in 1855, two years before his death.