
Zeta function
Encyclopedia
In mathematics
, a zeta
function is (usually) a function
analogous to the original example: the Riemann zeta function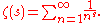
Zeta functions include:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a zeta
Zeta
-Science:* Zeta functions, in mathematics** Riemann zeta function* Zeta potential, the electrokinetic potential of a colloidal system* Tropical Storm Zeta , formed in December 2005 and lasting through January 2006* Z-pinch, in fusion power...
function is (usually) a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
analogous to the original example: the Riemann zeta function
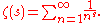
Zeta functions include:
- Airy zeta functionAiry zeta functionIn mathematics, the Airy zeta function, studied by , is a functions analogous to the Riemann zeta function and related to the zeros of the Airy function....
, related to the zeros of the Airy functionAiry functionIn the physical sciences, the Airy function Ai is a special function named after the British astronomer George Biddell Airy... - Artin–Mazur zeta-function of a dynamical system
- Barnes zeta functionBarnes zeta functionIn mathematics, a Barnes zeta function is a generalization of the Riemann zeta function introduced by . It is further generalized by the Shintani zeta function.-Definition:The Barnes zeta function is defined by...
- Beurling zeta functionBeurling zeta functionIn mathematics, a Beurling zeta function is an analogue of the Riemann zeta function where the ordinary primes are replaced by Beurling generalized primes: a sequence of real numbers greater than 1 that tend to infinity. These were introduced by ....
of Beurling generalized primes - Dedekind zeta-functionDedekind zeta functionIn mathematics, the Dedekind zeta function of an algebraic number field K, generally denoted ζK, is a generalization of the Riemann zeta function—which is obtained by specializing to the case where K is the rational numbers Q...
of a number field - Epstein zeta-function of a quadratic form.
- Goss zeta functionGoss zeta functionIn the field of mathematics, the Goss zeta function, named after David Goss, is an analogue of the Riemann zeta function for function fields. proved that it satisfies an analogue of the Riemann hypothesis....
of a function field - Hasse-Weil zeta-functionHasse-Weil zeta functionIn mathematics, the Hasse–Weil zeta function attached to an algebraic variety V defined over an algebraic number field K is one of the two most important types of L-function. Such L-functions are called 'global', in that they are defined as Euler products in terms of local zeta functions...
of a variety - Hurwitz zeta-function A generalization of the Riemann zeta function
- Ihara zeta-functionIhara zeta functionThe Ihara zeta-function is a zeta function associated with a finite graph. It closely resembles the Selberg zeta-function, and is used to relate closed paths to the spectrum of the adjacency matrix. The Ihara zeta-function was first defined by Yasutaka Ihara in the 1960s in the context of discrete...
of a graph - Igusa zeta-function
- Jacobi zeta functionJacobi zeta functionIn mathematics, the Jacobi zeta function Z is the logarithmic derivative of the Jacobi theta function Θ = θ4....
This is related to elliptic functions and is not analogous to the Riemann zeta function. - L-functionL-functionThe theory of L-functions has become a very substantial, and still largely conjectural, part of contemporary analytic number theory. In it, broad generalisations of the Riemann zeta function and the L-series for a Dirichlet character are constructed, and their general properties, in most cases...
, a 'twisted' zeta-function. - Lefschetz zeta-functionLefschetz zeta functionIn mathematics, the Lefschetz zeta-function is a tool used in topological periodic and fixed point theory, and dynamical systems. Given a mapping ƒ, the zeta-function is defined as the formal series...
of a morphism - Lerch zeta-functionLerch zeta functionIn mathematics, the Lerch zeta-function, sometimes called the Hurwitz–Lerch zeta-function, is a special function that generalizes the Hurwitz zeta-function and the polylogarithm...
A generalization of the Riemann zeta function - Local zeta-functionLocal zeta-functionIn number theory, a local zeta-functionis a function whose logarithmic derivative is a generating functionfor the number of solutions of a set of equations defined over a finite field F, in extension fields Fk of F.-Formulation:...
of a characteristic p variety - Matsumoto zeta function
- Minakshisundaram–Pleijel zeta function of a Laplacian
- Motivic zeta function of a motive
- Mordell-Tornheim zeta-function of several variables
- Multiple zeta function
- p-adic zeta function of a p-adic number
- Prime zeta function Like the Riemann zeta function, but only summed over primes.
- Riemann zeta function The archetypal example.
- Selberg zeta-function of a Riemann surface
- Shintani zeta functionShintani zeta functionIn mathematics, a Shintani zeta function or Shintani L-function is a generalization of the Riemann zeta function. They were studied studied by...
- Weierstrass zeta function This is related to elliptic functions and is not analogous to the Riemann zeta function.
- Witten zeta functionWitten zeta functionIn mathematics, the Witten zeta function, introduced by , is a function associated to a root system that encodes the degrees of the irreducible representations of the corresponding Lie group...
of a Lie group - Zeta function of an operator
See also
- Artin conjecture
- Birch and Swinnerton-Dyer conjectureBirch and Swinnerton-Dyer conjectureIn mathematics, the Birch and Swinnerton-Dyer conjecture is an open problem in the field of number theory. Its status as one of the most challenging mathematical questions has become widely recognized; the conjecture was chosen as one of the seven Millennium Prize Problems listed by the Clay...
- Riemann hypothesisRiemann hypothesisIn mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
and the generalized Riemann hypothesisGeneralized Riemann hypothesisThe Riemann hypothesis is one of the most important conjectures in mathematics. It is a statement about the zeros of the Riemann zeta function. Various geometrical and arithmetical objects can be described by so-called global L-functions, which are formally similar to the Riemann zeta-function...
. - Selberg class S

