
Lindelöf hypothesis
Encyclopedia
In mathematics, the Lindelöf hypothesis is a conjecture by Finnish mathematician Ernst Leonard Lindelöf
(see ) about the rate of growth of the Riemann zeta function on the critical line that is implied by the Riemann hypothesis
.
It says that, for any ε > 0,

as t tends to infinity (see O notation). Since ε can be replaced by a smaller value, we can also write the conjecture as, for any positive ε,

of all real numbers a such that ζ(σ + iT) = O(T a). It is trivial to check that μ(σ) = 0 for σ > 1, and the functional equation of the zeta function implies that μ(σ) = μ(1 − σ) − σ + 1/2. The Phragmen–Lindelöf theorem implies that μ is convex. The Lindelöf hypothesis states μ(1/2) = 0, which together with the above properties of μ implies that μ(σ) is 0 for σ ≥ 1/2 and 1/2 − σ for σ ≤ 1/2.
Lindelöf's convexity result together with μ(1) = 0 and μ(0) = 1/2 implies that 0 ≤ μ(1/2) ≤ 1/4. The upper bound of 1/4 was lowered by Hardy
and Littlewood to 1/6 by applying Weyl's method of estimating exponential sum
s to the approximate functional equation. It has since been lowered to slightly less than 1/6 by several authors using long and technical proofs, as in the following table:
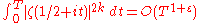
for all positive integers k and all positive real numbers ε. This has been proved for k = 1 or 2, but the case k = 3 seems much harder and is still an open problem.
There is a much more precise conjecture about the asymptotic behavior of this integral: it is believed that
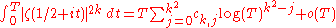
for some constants ck,j. This has been proved by Littlewood for k = 1 and by for k = 2
(extending a result of who found the leading term).
suggested the value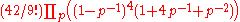 for the leading coefficient when k is 6, and used random matrix theory to suggest some conjectures for the values of the coefficients for higher k. The leading coefficients are conjectured to be the product of an elementary factor, a certain product over primes, and the number of n by n Young tableaux given by the following sequence:
for the leading coefficient when k is 6, and used random matrix theory to suggest some conjectures for the values of the coefficients for higher k. The leading coefficients are conjectured to be the product of an elementary factor, a certain product over primes, and the number of n by n Young tableaux given by the following sequence:
, shows that the Lindelöf hypothesis implies that, for any ε > 0,
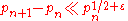
if n is sufficiently large. However, this result is much worse than that of the large prime gap conjecture.
Ernst Leonard Lindelöf
Ernst Leonard Lindelöf, was a Finnish topologist after whom Lindelöf spaces are named; he was the son of Leonard Lorenz Lindelöf and brother of the philologist Uno Lorenz Lindelöf....
(see ) about the rate of growth of the Riemann zeta function on the critical line that is implied by the Riemann hypothesis
Riemann hypothesis
In mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
.
It says that, for any ε > 0,

as t tends to infinity (see O notation). Since ε can be replaced by a smaller value, we can also write the conjecture as, for any positive ε,

The μ function
If σ is real, then μ(σ) is defined to be the infimumInfimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
of all real numbers a such that ζ(σ + iT) = O(T a). It is trivial to check that μ(σ) = 0 for σ > 1, and the functional equation of the zeta function implies that μ(σ) = μ(1 − σ) − σ + 1/2. The Phragmen–Lindelöf theorem implies that μ is convex. The Lindelöf hypothesis states μ(1/2) = 0, which together with the above properties of μ implies that μ(σ) is 0 for σ ≥ 1/2 and 1/2 − σ for σ ≤ 1/2.
Lindelöf's convexity result together with μ(1) = 0 and μ(0) = 1/2 implies that 0 ≤ μ(1/2) ≤ 1/4. The upper bound of 1/4 was lowered by Hardy
G. H. Hardy
Godfrey Harold “G. H.” Hardy FRS was a prominent English mathematician, known for his achievements in number theory and mathematical analysis....
and Littlewood to 1/6 by applying Weyl's method of estimating exponential sum
Exponential sum
In mathematics, an exponential sum may be a finite Fourier series , or other finite sum formed using the exponential function, usually expressed by means of the functione = \exp.\,...
s to the approximate functional equation. It has since been lowered to slightly less than 1/6 by several authors using long and technical proofs, as in the following table:
| μ(1/2) ≤ | μ(1/2) ≤ | Author | |
|---|---|---|---|
| 1/4 | 0.25 | Convexity bound | |
| 1/6 | 0.1667 | ||
| 163/988 | 0.1650 | ||
| 27/164 | 0.1647 | ||
| 229/1392 | 0.164512 | ||
| 0.164511 | |||
| 19/116 | 0.1638 | ||
| 15/92 | .1631 | ||
| 6/37 | .16217 | ||
| 173/1067 | 0.16214 | ||
| 35/216 | 0.16204 | ||
| 139/858 | 0.16201 | ||
| 32/205 | 0.1561 |
Relation to the Riemann hypothesis
showed that the Lindelöf hypothesis is equivalent to the following statement about the zeros of the zeta function: for every ε > 0, the number of zeros with real part at least 1/2 + ε and imaginary part between T and T + 1 is o(log(T)) as T tends to infinity. The Riemann hypothesis implies that there are no zeros at all in this region and so implies the Lindelöf hypothesis. The number of zeros with imaginary part between T and T + 1 is known to be O(log(T)), so the Lindelöf hypothesis seems only slightly stronger than what has already been proved, but in spite of this it has resisted all attempts to prove it and is very hard.Means of powers of the zeta function
The Lindelöf hypothesis is equivalent to the statement that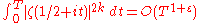
for all positive integers k and all positive real numbers ε. This has been proved for k = 1 or 2, but the case k = 3 seems much harder and is still an open problem.
There is a much more precise conjecture about the asymptotic behavior of this integral: it is believed that
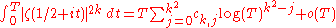
for some constants ck,j. This has been proved by Littlewood for k = 1 and by for k = 2
(extending a result of who found the leading term).
suggested the value
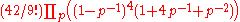 for the leading coefficient when k is 6, and used random matrix theory to suggest some conjectures for the values of the coefficients for higher k. The leading coefficients are conjectured to be the product of an elementary factor, a certain product over primes, and the number of n by n Young tableaux given by the following sequence:
for the leading coefficient when k is 6, and used random matrix theory to suggest some conjectures for the values of the coefficients for higher k. The leading coefficients are conjectured to be the product of an elementary factor, a certain product over primes, and the number of n by n Young tableaux given by the following sequence:
- 1, 1, 2, 42, 24024, 701149020, .
Other consequences
Denoting by pn the n-th prime number, a result by Albert InghamAlbert Ingham
Albert Edward Ingham was an English mathematician.Ingham was born in Northampton. He went to Stafford Grammar School and Trinity College, Cambridge . He obtained his Ph.D., which was supervised by John Edensor Littlewood, from the University of Cambridge. He supervised the Ph.D.s of C. Brian...
, shows that the Lindelöf hypothesis implies that, for any ε > 0,
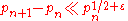
if n is sufficiently large. However, this result is much worse than that of the large prime gap conjecture.

