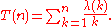
Liouville function
Encyclopedia
The Liouville function, denoted by λ(n) and named after Joseph Liouville
, is an important function
in number theory
.
If n is a positive integer
, then λ(n) is defined as:
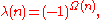
where Ω(n)
is the number of prime
factors
of n, counted with multiplicity .
λ is completely multiplicative
since Ω(n) is additive
. We have Ω(1) = 0 and therefore λ(1) = 1. The Liouville function satisfies the identity
:

The Liouville function's Dirichlet inverse is the absolute value of the Mobius function
.

The Lambert series for the Liouville function is
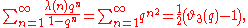
where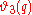 is the Jacobi theta function.
is the Jacobi theta function.
is a conjecture made by George Pólya
in 1919. Defining
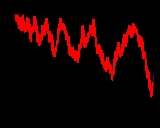
the conjecture states that for n > 1. This turned out to be false. The smallest counter-example is n = 906150257, found by Minoru Tanaka in 1980. It has since been shown that L(n) > 0.0618672√n for infinitely many positive integers n, while it can also be shown that L(n) < -1.3892783√n for infinitely many positive integers n.
for n > 1. This turned out to be false. The smallest counter-example is n = 906150257, found by Minoru Tanaka in 1980. It has since been shown that L(n) > 0.0618672√n for infinitely many positive integers n, while it can also be shown that L(n) < -1.3892783√n for infinitely many positive integers n.
Define the related sum
It was open for some time whether T(n) ≥ 0 for sufficiently big n ≥ n0 (this "conjecture" is occasionally (but incorrectly) attributed to Pál Turán
). This was then disproved by Haselgrove
in 1958 (see the reference below), who showed that T(n) takes negative values infinitely often. A confirmation of this positivity conjecture would have led to a proof of the Riemann hypothesis
, as was shown by Pál Turán.
Joseph Liouville
- Life and work :Liouville graduated from the École Polytechnique in 1827. After some years as an assistant at various institutions including the Ecole Centrale Paris, he was appointed as professor at the École Polytechnique in 1838...
, is an important function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
in number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
.
If n is a positive integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
, then λ(n) is defined as:
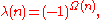
where Ω(n)
Big Omega function
The notation \Omega \,\! has at least three meanings in mathematics:* f = \Omega \,\! means that the function f\,\! dominates g\,\! in some limit, see Big O notation...
is the number of prime
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
factors
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
of n, counted with multiplicity .
λ is completely multiplicative
Multiplicative function
In number theory, a multiplicative function is an arithmetic function f of the positive integer n with the property that f = 1 and whenevera and b are coprime, then...
since Ω(n) is additive
Additive function
In mathematics the term additive function has two different definitions, depending on the specific field of application.In algebra an additive function is a function that preserves the addition operation:for any two elements x and y in the domain. For example, any linear map is additive...
. We have Ω(1) = 0 and therefore λ(1) = 1. The Liouville function satisfies the identity
Identity (mathematics)
In mathematics, the term identity has several different important meanings:*An identity is a relation which is tautologically true. This means that whatever the number or value may be, the answer stays the same. For example, algebraically, this occurs if an equation is satisfied for all values of...
:

The Liouville function's Dirichlet inverse is the absolute value of the Mobius function
Möbius function
The classical Möbius function μ is an important multiplicative function in number theory and combinatorics. The German mathematician August Ferdinand Möbius introduced it in 1832...
.
Series
The Dirichlet series for the Liouville function gives the Riemann zeta function as
The Lambert series for the Liouville function is
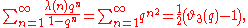
where
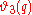 is the Jacobi theta function.
is the Jacobi theta function.Conjectures
The Pólya conjecturePólya conjecture
In number theory, the Pólya conjecture stated that 'most' of the natural numbers less than any given number have an odd number of prime factors. The conjecture was posited by the Hungarian mathematician George Pólya in 1919, and proved false in 1958...
is a conjecture made by George Pólya
George Pólya
George Pólya was a Hungarian mathematician. He was a professor of mathematics from 1914 to 1940 at ETH Zürich and from 1940 to 1953 at Stanford University. He made fundamental contributions to combinatorics, number theory, numerical analysis and probability theory...
in 1919. Defining
the conjecture states that
 for n > 1. This turned out to be false. The smallest counter-example is n = 906150257, found by Minoru Tanaka in 1980. It has since been shown that L(n) > 0.0618672√n for infinitely many positive integers n, while it can also be shown that L(n) < -1.3892783√n for infinitely many positive integers n.
for n > 1. This turned out to be false. The smallest counter-example is n = 906150257, found by Minoru Tanaka in 1980. It has since been shown that L(n) > 0.0618672√n for infinitely many positive integers n, while it can also be shown that L(n) < -1.3892783√n for infinitely many positive integers n.Define the related sum
It was open for some time whether T(n) ≥ 0 for sufficiently big n ≥ n0 (this "conjecture" is occasionally (but incorrectly) attributed to Pál Turán
Pál Turán
Paul Turán was a Hungarian mathematician who worked primarily in number theory. He had a long collaboration with fellow Hungarian mathematician Paul Erdős, lasting 46 years and resulting in 28 joint papers.- Life and education :...
). This was then disproved by Haselgrove
C. Brian Haselgrove
Colin Brian Haselgrove was an English mathematician who is best known for his disproof of the Pólya conjecture in 1958....
in 1958 (see the reference below), who showed that T(n) takes negative values infinitely often. A confirmation of this positivity conjecture would have led to a proof of the Riemann hypothesis
Riemann hypothesis
In mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
, as was shown by Pál Turán.