
Ihara zeta function
Encyclopedia
The Ihara zeta-function is a zeta function associated with a finite graph
. It closely resembles the Selberg zeta-function, and is used to relate closed paths to the spectrum of the adjacency matrix
. The Ihara zeta-function was first defined by Yasutaka Ihara in the 1960s in the context of discrete subgroups
of the two-by-two p-adic
special linear group
. Jean-Pierre Serre
suggested in his book Trees that Ihara's original definition can be reinterpreted graph-theoretically. It was Toshikazu Sunada
who put this suggestion into practice (1985). A regular graph
is a Ramanujan graph
if and only if its Ihara zeta function satisfies an analogue of the Riemann hypothesis
.
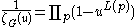
This product is taken over all prime walks p of the graph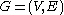 - that is, closed cycles
- that is, closed cycles 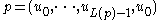 such that
such that
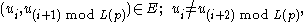
and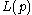 is the length of cycle p, as used in the formulae above.
is the length of cycle p, as used in the formulae above.

where T is Hashimoto's edge adjacency operator. Hyman Bass
gave a determinant formula involving the adjacency operator.
s, spectral graph theory
, and dynamical systems, especially symbolic dynamics
.
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
. It closely resembles the Selberg zeta-function, and is used to relate closed paths to the spectrum of the adjacency matrix
Adjacency matrix
In mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...
. The Ihara zeta-function was first defined by Yasutaka Ihara in the 1960s in the context of discrete subgroups
Discrete group
In mathematics, a discrete group is a group G equipped with the discrete topology. With this topology G becomes a topological group. A discrete subgroup of a topological group G is a subgroup H whose relative topology is the discrete one...
of the two-by-two p-adic
P-adic number
In mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
special linear group
Special linear group
In mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion....
. Jean-Pierre Serre
Jean-Pierre Serre
Jean-Pierre Serre is a French mathematician. He has made contributions in the fields of algebraic geometry, number theory, and topology.-Early years:...
suggested in his book Trees that Ihara's original definition can be reinterpreted graph-theoretically. It was Toshikazu Sunada
Toshikazu Sunada
is a Japanese mathematician and author of many books and essays on mathematics and mathematical sciences. He is professor of mathematics at Meiji University, Tokyo, and is also professor emeritus of Tohoku University, Tohoku, Japan...
who put this suggestion into practice (1985). A regular graph
Regular graph
In graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other...
is a Ramanujan graph
Ramanujan graph
A Ramanujan graph, named after Srinivasa Ramanujan, is a regular graph whose spectral gap is almost as large as possible . Such graphs are excellent spectral expanders....
if and only if its Ihara zeta function satisfies an analogue of the Riemann hypothesis
Riemann hypothesis
In mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
.
Definition
The Ihara zeta-function can be defined by a formula analogous to the Euler product for the Riemann zeta function: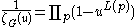
This product is taken over all prime walks p of the graph
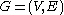 - that is, closed cycles
- that is, closed cycles 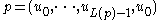 such that
such that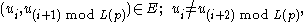
and
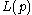 is the length of cycle p, as used in the formulae above.
is the length of cycle p, as used in the formulae above.Ihara's formula
The Ihara zeta-function is in fact always the reciprocal of a polynomial:
where T is Hashimoto's edge adjacency operator. Hyman Bass
Hyman Bass
Hyman Bass is an American mathematician, known for work in algebra and in mathematics education. From 1959-1998 he was Professor in the Mathematics Department at Columbia University, where he is now professor emeritus...
gave a determinant formula involving the adjacency operator.
Applications
The Ihara zeta-function plays an important role in the study of free groupFree group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
s, spectral graph theory
Spectral graph theory
In mathematics, spectral graph theory is the study of properties of a graph in relationship to the characteristic polynomial, eigenvalues, and eigenvectors of matrices associated to the graph, such as its adjacency matrix or Laplacian matrix....
, and dynamical systems, especially symbolic dynamics
Symbolic dynamics
In mathematics, symbolic dynamics is the practice of modeling a topological or smooth dynamical system by a discrete space consisting of infinite sequences of abstract symbols, each of which corresponds to a state of the system, with the dynamics given by the shift operator...
.

