
Lax pair
Encyclopedia
In mathematics
, in the theory of integrable systems, a Lax pair is a pair of time-dependent matrices or operators that describe the corresponding differential equation
s. They were introduced by Peter Lax
to discuss soliton
s in continuous media. The inverse scattering transform
makes use of the Lax equations to solve such systems.
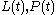 dependent on time and acting on a fixed Hilbert space
dependent on time and acting on a fixed Hilbert space
, and verifying the Lax's equation:

where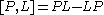 is the commutator
is the commutator
.
Often, as in the example below,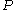 depends on
depends on 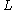 in a prescribed way, so this is a nonlinear equation for
in a prescribed way, so this is a nonlinear equation for 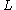 as a function of
as a function of  .
.
as varies.
varies.
The core observation is that the matrices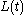 are all similar by virtue of
are all similar by virtue of
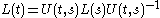
where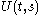 is the solution of the Cauchy problem
is the solution of the Cauchy problem
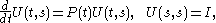
where I denotes the identity matrix. Note that if L(t) is self-adjoint
and P(t) is skew-adjoint, then U(t,s) will be unitary
.
In other words, to solve the eigenvalue problem Lψ = λψ at time t, it is possible to solve the same problem at time 0 where L is generally known better, and to propagate the solution with the following formulas: (no change in spectrum)
(no change in spectrum)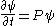
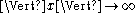 .
.
The method then takes the following form:
is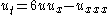
It can be reformulated as the Lax equation
with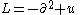 (a Sturm–Liouville operator)
(a Sturm–Liouville operator)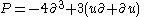
where all derivatives act on all objects to the right. This accounts for the infinite number of first integrals of the KdV equation.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the theory of integrable systems, a Lax pair is a pair of time-dependent matrices or operators that describe the corresponding differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s. They were introduced by Peter Lax
Peter Lax
Peter David Lax is a mathematician working in the areas of pure and applied mathematics. He has made important contributions to integrable systems, fluid dynamics and shock waves, solitonic physics, hyperbolic conservation laws, and mathematical and scientific computing, among other fields...
to discuss soliton
Soliton
In mathematics and physics, a soliton is a self-reinforcing solitary wave that maintains its shape while it travels at constant speed. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium...
s in continuous media. The inverse scattering transform
Inverse scattering transform
In mathematics, the inverse scattering transform is a method for solving some non-linear partial differential equations. It is one of the most important developments in mathematical physics in the past 40 years...
makes use of the Lax equations to solve such systems.
Definition
A Lax pair is a pair of matrices or operators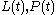 dependent on time and acting on a fixed Hilbert space
dependent on time and acting on a fixed Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
, and verifying the Lax's equation:

where
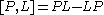 is the commutator
is the commutatorCommutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
.
Often, as in the example below,
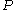 depends on
depends on 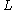 in a prescribed way, so this is a nonlinear equation for
in a prescribed way, so this is a nonlinear equation for 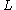 as a function of
as a function of  .
.Isospectral property
It can then be shown that the eigenvalues and more generally the spectrum of L are independent of t. The matrices/operators L are said to be isospectralIsospectral
In mathematics, two linear operators are called isospectral or cospectral if they have the same spectrum. Roughly speaking, they are supposed to have the same sets of eigenvalues, when those are counted with multiplicity....
as
 varies.
varies.The core observation is that the matrices
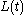 are all similar by virtue of
are all similar by virtue of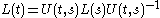
where
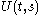 is the solution of the Cauchy problem
is the solution of the Cauchy problemCauchy problem
A Cauchy problem in mathematics asks for the solution of a partial differential equation that satisfies certain conditions which are given on a hypersurface in the domain. Cauchy problems are an extension of initial value problems and are to be contrasted with boundary value problems...
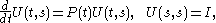
where I denotes the identity matrix. Note that if L(t) is self-adjoint
Self-adjoint
In mathematics, an element x of a star-algebra is self-adjoint if x^*=x.A collection C of elements of a star-algebra is self-adjoint if it is closed under the involution operation...
and P(t) is skew-adjoint, then U(t,s) will be unitary
Unitary
Unitary may refer to:* Unitary construction, in automotive design, another common term for a unibody or monocoque construction**Unitary as chemical weapons opposite of Binary...
.
In other words, to solve the eigenvalue problem Lψ = λψ at time t, it is possible to solve the same problem at time 0 where L is generally known better, and to propagate the solution with the following formulas:
 (no change in spectrum)
(no change in spectrum)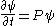
Link with the inverse scattering method
The above property is the basis for the inverse scattering method. In this method, L and P act on a functional space (thus ψ = ψ(t,x)), and depend on an unknown function u(t,x) which is to be determined. It is generally assumed that u(0,x) is known, and that P does not depend on u in the scattering region where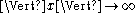 .
.The method then takes the following form:
- Compute the spectrum of
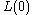 , giving
, giving 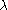 and
and 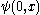 ,
, - In the scattering region where
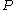 is known, propagate
is known, propagate 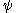 by using
by using  with initial condition
with initial condition 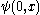 ,
, - Knowing
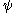 in the scattering region, compute
in the scattering region, compute 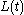 and/or
and/or  .
.
Example
The Korteweg–de Vries equationKorteweg–de Vries equation
In mathematics, the Korteweg–de Vries equation is a mathematical model of waves on shallow water surfaces. It is particularly notable as the prototypical example of an exactly solvable model, that is, a non-linear partial differential equation whose solutions can be exactly and precisely specified...
is
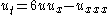
It can be reformulated as the Lax equation

with
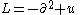 (a Sturm–Liouville operator)
(a Sturm–Liouville operator)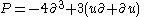
where all derivatives act on all objects to the right. This accounts for the infinite number of first integrals of the KdV equation.
Equations with a Lax pair
Further examples of systems of equations that can be formulated as a Lax pair include:- Benjamin–Ono equation
- One dimensional cubic non-linear Schrödinger equation
- Davey-Stewartson system
- Kadomtsev–Petviashvili equation
- Korteweg–de Vries equationKorteweg–de Vries equationIn mathematics, the Korteweg–de Vries equation is a mathematical model of waves on shallow water surfaces. It is particularly notable as the prototypical example of an exactly solvable model, that is, a non-linear partial differential equation whose solutions can be exactly and precisely specified...
- KdV hierarchy
- Modified Korteweg-de Vries equation
- Sine-Gordon equationSine-Gordon equationThe sine–Gordon equation is a nonlinear hyperbolic partial differential equation in 1 + 1 dimensions involving the d'Alembert operator and the sine of the unknown function. It was originally considered in the nineteenth century in the course of study of surfaces of constant negative...
- Toda lattice

