
Uniqueness quantification
Encyclopedia
In mathematics
and logic
, the phrase "there is one and only one" is used to indicate that exactly one object with a certain property exists. In mathematical logic
, this sort of quantification
is known as uniqueness quantification or unique existential quantification.
Uniqueness quantification is often denoted with the symbols "∃!" or ∃=1". For example, the formal statement
may be read aloud as "there is exactly one natural number n such that n - 2 = 4".
As a simple high school example, to show x + 2 = 5 has only one solution, we assume there are two solutions first, namely, a and b, satisfying x + 2 = 5. Thus
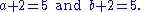
By transitivity of equality,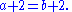
By cancellation,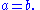
This simple example shows how a proof of uniqueness is done, the end result being the equality of the two quantities that satisfy the condition. We must say, however, that existence/expressibility must be proven before uniqueness, or else we cannot even assume the existence of those two quantities to begin with.
by defining the formula
∃!x P(x) to mean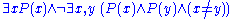
where an equivalence is: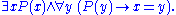
An equivalent definition that has the virtue of separating the notions of existence and uniqueness into two clauses, at the expense of brevity, is
Another equivalent definition with the advantage of brevity is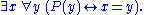
. This includes both quantification of the form "exactly k objects exist such that …" as well as "infinitely many objects exist such that …" and "only finitely many objects exist such that…". The first of these forms is expressible using ordinary quantifiers, but the latter two cannot be expressed in ordinary first-order logic
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and logic
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
, the phrase "there is one and only one" is used to indicate that exactly one object with a certain property exists. In mathematical logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, this sort of quantification
Quantification
Quantification has several distinct senses. In mathematics and empirical science, it is the act of counting and measuring that maps human sense observations and experiences into members of some set of numbers. Quantification in this sense is fundamental to the scientific method.In logic,...
is known as uniqueness quantification or unique existential quantification.
Uniqueness quantification is often denoted with the symbols "∃!" or ∃=1". For example, the formal statement
may be read aloud as "there is exactly one natural number n such that n - 2 = 4".
Proving uniqueness
Proving uniqueness turns out to be mostly easier than that of existence or expressibility. The most common technique to proving uniqueness is to assume there exists two quantities (say, a and b) that satisfies the condition given, and then logically deducing their equality, i.e. a = b.As a simple high school example, to show x + 2 = 5 has only one solution, we assume there are two solutions first, namely, a and b, satisfying x + 2 = 5. Thus
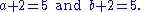
By transitivity of equality,
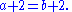
By cancellation,
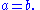
This simple example shows how a proof of uniqueness is done, the end result being the equality of the two quantities that satisfy the condition. We must say, however, that existence/expressibility must be proven before uniqueness, or else we cannot even assume the existence of those two quantities to begin with.
Reduction to ordinary existential and universal quantification
Uniqueness quantification can be expressed in terms of the existential and universal quantifiers of predicate logicPredicate logic
In mathematical logic, predicate logic is the generic term for symbolic formal systems like first-order logic, second-order logic, many-sorted logic or infinitary logic. This formal system is distinguished from other systems in that its formulae contain variables which can be quantified...
by defining the formula
∃!x P(x) to mean
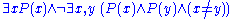
where an equivalence is:
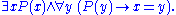
An equivalent definition that has the virtue of separating the notions of existence and uniqueness into two clauses, at the expense of brevity, is

Another equivalent definition with the advantage of brevity is
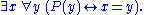
Generalizations
One generalization of uniqueness quantification is counting quantificationCounting quantification
A counting quantifier is a mathematical term for a quantifier of the form "there exists at least k elements that satisfy property X".In first-order logic with equality, counting quantifiers can be defined in terms of ordinary quantifiers, so in this context they are a notational shorthand.However,...
. This includes both quantification of the form "exactly k objects exist such that …" as well as "infinitely many objects exist such that …" and "only finitely many objects exist such that…". The first of these forms is expressible using ordinary quantifiers, but the latter two cannot be expressed in ordinary first-order logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
.


