Nonlinear Schrödinger equation
Encyclopedia
In theoretical physics
, the nonlinear Schrödinger equation (NLS) is a nonlinear version of Schrödinger's equation
. It is a classical field equation with applications to optics
and water waves. Unlike the Schrödinger equation, it never describes the time evolution of a quantum state. It is an example of an integrable model.
In quantum mechanics
, it is a special case of the nonlinear Schrödinger field
, and when canonically quantized, it describes bosonic point particles with delta-function interactions — the particles either repel or attract when they are at the same point. The nonlinear Schrödinger equation is integrable when the particles move in one dimension of space. In the limit of infinite strength repulsion, the nonlinear Schrödinger equation bosons are equivalent to one dimensional free fermions.
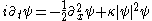
for the complex
field ψ(x,t).
This equation arises from the Hamiltonian
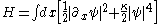
with the Poisson bracket
s
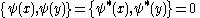
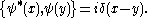
, simply replace the Poisson brackets by commutators
and normal order
the Hamiltonian
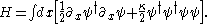
The quantum version was solved by Bethe ansatz
by Lieb and Liniger
. Thermodynamics was described by
Chen Nin Yang. Quantum correlation functions also were evaluated, see.
The model has higher conservation laws, expression in terms of local fields can be found in. http://insti.physics.sunysb.edu/~korepin/davis.pdf.
. The corresponding linear system of equations is known as the Zakharov–Shabat system:
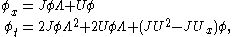
where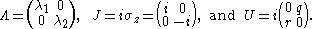
The nonlinear Schrödinger equation arises as compatibility condition of the Zakharov–Shabat system:
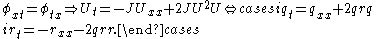
By setting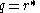
or 
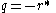the
nonlinear Schrödinger equation with attractive or repulsive
interaction is obtained.
An alternative approach uses the Zakharov–Shabat system directly and employs the following Darboux transformation:
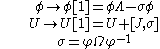
which leaves the system invariant.
Here,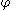
is another invertible matrix solution (different from 
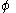) of the Zakharov–Shabat system with spectral parameter 
:
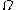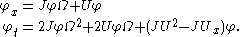
Starting from the trivial solution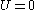
and iterating, one obtains the solutions with n soliton
s.
Computational solutions are found using a variety of methods, like the split-step method
.
in the following sense:
Given a solution
a new solution can be obtained by replacing 
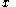with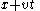 
everywhere in 
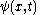and by appending a phase factor of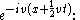 
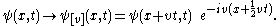
, the nonlinear Schrödinger equation occurs in the Manakov system
, a model of wave propagation in fiber optics. The function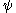
represents a wave and the nonlinear Schrödinger equation describes the propagation of the wave through a nonlinear medium. The second-order derivative represents the dispersion, while the κ term represents the nonlinearity. The equation models many nonlinearity effects in a fiber, including but not limited to self-phase modulation
, four-wave mixing
, second harmonic generation
, stimulated Raman scattering
, etc.
For water waves, the nonlinear Schrödinger equation describes the evolution of the envelope
of modulated
wave groups. In a paper in 1968, Vladimir E. Zakharov
describes the Hamiltonian
structure of water waves. In the same paper Zakharov shows, that for slowly-modulated wave groups, the wave amplitude
satisfies the nonlinear Schrödinger equation, approximately. The value of the nonlinearity parameter к depends on the relative water depth. For deep water, with the water depth large compared to the wave length of the water waves, к is negative and envelope
soliton
s may occur.
For shallow water, with wavelengths longer than 4.6 times the water depth, the nonlinearity parameter к is positive and wave groups with envelope solitons do not exist. Note, that in shallow water surface-elevation solitons or waves of translation do exist, but they are not governed by the nonlinear Schrödinger equation.
The nonlinear Schrödinger equation is thought to be important for explaining the formation of rogue waves.
The complex
field ψ, as appearing in the nonlinear Schrödinger equation, is related to the amplitude and phase of the water waves. Consider a slowly-modulated carrier wave
with water surface elevation
η of the form: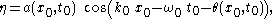
where a( x0 , t0 ) and θ( x0 , t0 ) are the slowly-modulated amplitude and phase
. Further ω0 and k0 are the (constant) angular frequency
and wavenumber
of the carrier waves, which have to satisfy the dispersion
relation ω0 = Ω( k0 ). Then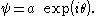
So its modulus |ψ| is the wave amplitude a, and its argument arg(ψ) is the phase θ.
The relation between the physical coordinates ( x0 , t0 ) and the ( x , t ) coordinates, as used in the nonlinear Schrödinger equation given above, is given by: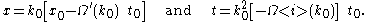
Thus ( x, t ) is a transformed coordinate system moving with the group velocity
Ω'( k0 ) of the carrier waves,
The dispersion-relation curvature
Ω"( k0 ) is always negative for water waves under the action of gravity.
For waves on the water surface of deep water, the coefficients of importance for the nonlinear Schrödinger equation are: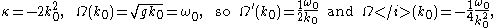
with g the acceleration by gravity
.
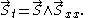
Note that this equation admits several integrable and non-integrable generalizations in 2+1 dimensions like the Ishimori equation
and so on.
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, the nonlinear Schrödinger equation (NLS) is a nonlinear version of Schrödinger's equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
. It is a classical field equation with applications to optics
Optics
Optics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light...
and water waves. Unlike the Schrödinger equation, it never describes the time evolution of a quantum state. It is an example of an integrable model.
In quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, it is a special case of the nonlinear Schrödinger field
Schrödinger field
In quantum mechanics and quantum field theory, a Schrödinger field, named after Erwin Schrödinger, is a quantum field which obeys the Schrödinger equation...
, and when canonically quantized, it describes bosonic point particles with delta-function interactions — the particles either repel or attract when they are at the same point. The nonlinear Schrödinger equation is integrable when the particles move in one dimension of space. In the limit of infinite strength repulsion, the nonlinear Schrödinger equation bosons are equivalent to one dimensional free fermions.
The equation
The nonlinear Schrödinger equation is the partial differential equationPartial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
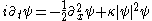
for the complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
field ψ(x,t).
This equation arises from the Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
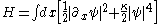
with the Poisson bracket
Poisson bracket
In mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time-evolution of a Hamiltonian dynamical system...
s
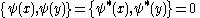
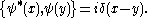
Quantum version
To get the quantized versionSchrödinger field
In quantum mechanics and quantum field theory, a Schrödinger field, named after Erwin Schrödinger, is a quantum field which obeys the Schrödinger equation...
, simply replace the Poisson brackets by commutators
and normal order
Normal order
In quantum field theory a product of quantum fields, or equivalently their creation and annihilation operators, is usually said to be normal ordered when all creation operators are to the left of all annihilation operators in the product. The process of putting a product into normal order is...
the Hamiltonian
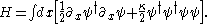
The quantum version was solved by Bethe ansatz
Bethe ansatz
In physics, the Bethe ansatz is a method for finding the exact solutions of certain one-dimensional quantum many-body models. It was invented by Hans Bethe in 1931 to find the exact eigenvalues and eigenvectors of the one-dimensional antiferromagnetic Heisenberg model Hamiltonian...
by Lieb and Liniger
Lieb-Liniger Model
The Lieb–Liniger model describes a gas of particles moving in one dimension and satisfying Bose–Einstein statistics.-Introduction:A model of a gas of particles moving in one dimension and satisfying...
. Thermodynamics was described by
Chen Nin Yang. Quantum correlation functions also were evaluated, see.
The model has higher conservation laws, expression in terms of local fields can be found in. http://insti.physics.sunysb.edu/~korepin/davis.pdf.
Solving the equation
The nonlinear Schrödinger equation is integrable: It can be solved with the inverse scattering transformInverse scattering transform
In mathematics, the inverse scattering transform is a method for solving some non-linear partial differential equations. It is one of the most important developments in mathematical physics in the past 40 years...
. The corresponding linear system of equations is known as the Zakharov–Shabat system:
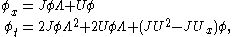
where
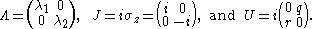
The nonlinear Schrödinger equation arises as compatibility condition of the Zakharov–Shabat system:
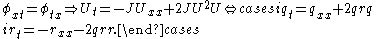
By setting
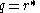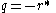or thenonlinear Schrödinger equation with attractive or repulsive
interaction is obtained.
An alternative approach uses the Zakharov–Shabat system directly and employs the following Darboux transformation:
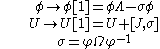
which leaves the system invariant.
Here,
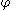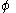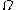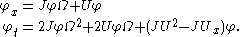
is another invertible matrix solution (different from ) of the Zakharov–Shabat system with spectral parameter :Starting from the trivial solution
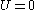and iterating, one obtains the solutions with n solitonSoliton
In mathematics and physics, a soliton is a self-reinforcing solitary wave that maintains its shape while it travels at constant speed. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium...
s.
Computational solutions are found using a variety of methods, like the split-step method
Split-step method
In numerical analysis, the split-step method is a pseudo-spectral numerical method used to solve nonlinear partial differential equations like the nonlinear Schrödinger equation. The name arises for two reasons. First, the method relies on computing the solution in small steps, and treating the...
.
Galilean invariance
The nonlinear Schrödinger equation is Galilean invariantGalilean invariance
Galilean invariance or Galilean relativity is a principle of relativity which states that the fundamental laws of physics are the same in all inertial frames...
in the following sense:
Given a solution
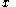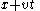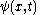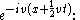
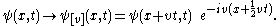
a new solution can be obtained by replacing with everywhere in and by appending a phase factor of The nonlinear Schrödinger equation in fiber optics
In opticsOptics
Optics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light...
, the nonlinear Schrödinger equation occurs in the Manakov system
Manakov system
Maxwell's Equations, when converted to cylindrical coordinates, and with the boundary conditions for an optical fiber while including birefringence as an effect taken into account, will yield the coupled nonlinear Schrödinger equations...
, a model of wave propagation in fiber optics. The function
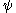represents a wave and the nonlinear Schrödinger equation describes the propagation of the wave through a nonlinear medium. The second-order derivative represents the dispersion, while the κ term represents the nonlinearity. The equation models many nonlinearity effects in a fiber, including but not limited to self-phase modulationSelf-phase modulation
Self-phase modulation is a nonlinear optical effect of light-matter interaction.An ultrashort pulse of light, when travelling in a medium, will induce a varying refractive index of the medium due to the optical Kerr effect...
, four-wave mixing
Four-wave mixing
Four-wave mixing is an intermodulation phenomenon in optical systems, whereby interactions between 3 wavelengths produce a 4th wavelength in the signal. It is similar to the third-order intercept point in electrical systems...
, second harmonic generation
Second harmonic generation
An optical frequency multiplier is a nonlinear optical device, in which photons interacting with a nonlinear material are effectively "combined" to form new photons with greater energy, and thus higher frequency...
, stimulated Raman scattering
Raman scattering
Raman scattering or the Raman effect is the inelastic scattering of a photon. It was discovered by Sir Chandrasekhara Venkata Raman and Kariamanickam Srinivasa Krishnan in liquids, and by Grigory Landsberg and Leonid Mandelstam in crystals....
, etc.
The nonlinear Schrödinger equation in water waves
Envelope (mathematics)
In geometry, an envelope of a family of curves in the plane is a curve that is tangent to each member of the family at some point. Classically, a point on the envelope can be thought of as the intersection of two "adjacent" curves, meaning the limit of intersections of nearby curves...
of modulated
Modulation
In electronics and telecommunications, modulation is the process of varying one or more properties of a high-frequency periodic waveform, called the carrier signal, with a modulating signal which typically contains information to be transmitted...
wave groups. In a paper in 1968, Vladimir E. Zakharov
Vladimir E. Zakharov
Vladimir Evgen'evich Zakharov is a Soviet and Russian mathematician and physicist. He is currently Regents' Professor of mathematics at The University of Arizona and director of the Mathematical Physics Sector at the Lebedev Physical Institute...
describes the Hamiltonian
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
structure of water waves. In the same paper Zakharov shows, that for slowly-modulated wave groups, the wave amplitude
Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
satisfies the nonlinear Schrödinger equation, approximately. The value of the nonlinearity parameter к depends on the relative water depth. For deep water, with the water depth large compared to the wave length of the water waves, к is negative and envelope
Envelope (mathematics)
In geometry, an envelope of a family of curves in the plane is a curve that is tangent to each member of the family at some point. Classically, a point on the envelope can be thought of as the intersection of two "adjacent" curves, meaning the limit of intersections of nearby curves...
soliton
Soliton
In mathematics and physics, a soliton is a self-reinforcing solitary wave that maintains its shape while it travels at constant speed. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium...
s may occur.
For shallow water, with wavelengths longer than 4.6 times the water depth, the nonlinearity parameter к is positive and wave groups with envelope solitons do not exist. Note, that in shallow water surface-elevation solitons or waves of translation do exist, but they are not governed by the nonlinear Schrödinger equation.
The nonlinear Schrödinger equation is thought to be important for explaining the formation of rogue waves.
The complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
field ψ, as appearing in the nonlinear Schrödinger equation, is related to the amplitude and phase of the water waves. Consider a slowly-modulated carrier wave
Carrier wave
In telecommunications, a carrier wave or carrier is a waveform that is modulated with an input signal for the purpose of conveying information. This carrier wave is usually a much higher frequency than the input signal...
with water surface elevation
Elevation
The elevation of a geographic location is its height above a fixed reference point, most commonly a reference geoid, a mathematical model of the Earth's sea level as an equipotential gravitational surface ....
η of the form:
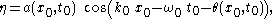
where a( x0 , t0 ) and θ( x0 , t0 ) are the slowly-modulated amplitude and phase
Phase (waves)
Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:...
. Further ω0 and k0 are the (constant) angular frequency
Angular frequency
In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
and wavenumber
Wavenumber
In the physical sciences, the wavenumber is a property of a wave, its spatial frequency, that is proportional to the reciprocal of the wavelength. It is also the magnitude of the wave vector...
of the carrier waves, which have to satisfy the dispersion
Dispersion (water waves)
In fluid dynamics, dispersion of water waves generally refers to frequency dispersion, which means that waves of different wavelengths travel at different phase speeds. Water waves, in this context, are waves propagating on the water surface, and forced by gravity and surface tension...
relation ω0 = Ω( k0 ). Then
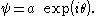
So its modulus |ψ| is the wave amplitude a, and its argument arg(ψ) is the phase θ.
The relation between the physical coordinates ( x0 , t0 ) and the ( x , t ) coordinates, as used in the nonlinear Schrödinger equation given above, is given by:
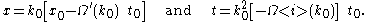
Thus ( x, t ) is a transformed coordinate system moving with the group velocity
Group velocity
The group velocity of a wave is the velocity with which the overall shape of the wave's amplitudes — known as the modulation or envelope of the wave — propagates through space....
Ω'( k0 ) of the carrier waves,
The dispersion-relation curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
Ω"( k0 ) is always negative for water waves under the action of gravity.
For waves on the water surface of deep water, the coefficients of importance for the nonlinear Schrödinger equation are:
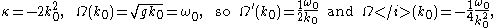
with g the acceleration by gravity
Earth's gravity
The gravity of Earth, denoted g, refers to the acceleration that the Earth imparts to objects on or near its surface. In SI units this acceleration is measured in metres per second per second or equivalently in newtons per kilogram...
.
Gauge equivalent counterpart
NLSE (1) is gauge equivalent to the following isotropic Landau-Lifshitz equation (LLE) or Heisenberg ferromagnet equation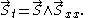Note that this equation admits several integrable and non-integrable generalizations in 2+1 dimensions like the Ishimori equation
Ishimori equation
The Ishimori equation is a partial differential equation proposed by the Japanese mathematician . Its interest is as the first example of a nonlinear spin-one field model in the plane that is integrable .-Equation:The IE has the form...
and so on.
See also
- Phi to the fourth for a related model in quantum field theoryQuantum field theoryQuantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
- Mathematical aspects of the nonlinear Schrödinger equation, on Dispersive Wiki
External links
- Nonlinear Schrodinger Equation with a Cubic Nonlinearity at EqWorld: The World of Mathematical Equations.
- Nonlinear Schrodinger Equation with a Power-Law Nonlinearity at EqWorld: The World of Mathematical Equations.
- Nonlinear Schrodinger Equation of General Form at EqWorld: The World of Mathematical Equations. Originally in: Zhurnal Prikdadnoi Mekhaniki i Tekhnicheskoi Fiziki 9 (2): 86–94, 1968.
- Fluid Mechanics by Falkovich, Section 3.3