
Robin boundary condition
Encyclopedia
In mathematics
, the Robin (or third type) boundary condition is a type of boundary condition, named after Victor Gustave Robin
(1855–1897). When imposed on an ordinary
or a partial differential equation
, it is a specification of a linear combination
of the values of a function
and the values of its derivative on the boundary
of the domain. Robin should be pronounced as a French
name (ʁoˈbɛ̃), although many English
-speaking mathematicians anglicize the word (ˈrɔːbɪn).
Robin boundary conditions are a weighed combination of Dirichlet boundary condition
s and Neumann boundary condition
s. This contrasts to mixed boundary condition
s, which are boundary conditions of different types specified on different subsets of the boundary. Robin boundary conditions are also called impedance boundary conditions, from their application in electromagnetic
problems.
If Ω is the domain on which the given equation is to be solved and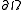 denotes its boundary
denotes its boundary
, the Robin boundary condition is: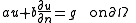
for some non-zero constants a and b and a given function g defined on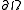 . Here, u is the unknown solution defined on
. Here, u is the unknown solution defined on  and
and 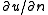 denotes the normal derivative at the boundary. More generally, a and b are allowed to be (given) functions, rather than constants.
denotes the normal derivative at the boundary. More generally, a and b are allowed to be (given) functions, rather than constants.
In one dimension, if, for example,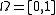 , the Robin boundary condition becomes the conditions:
, the Robin boundary condition becomes the conditions: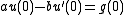
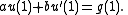
notice the change of sign in front of the term involving a derivative: that is because the normal to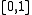 at 0 points in the negative direction, while at 1 it points in the positive direction.
at 0 points in the negative direction, while at 1 it points in the positive direction.
Robin boundary conditions are commonly used in solving Sturm–Liouville problems which appear in many contexts in science and engineering.
In addition, the Robin boundary condition is a general form of the insulating boundary condition for convection–diffusion equation
s. Here, the convective and diffusive fluxes at the boundary sum to zero:
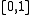
where D is the diffusive constant, u is the convective velocity at the boundary and c is the concentration. The first term is a result of Fick's law of diffusion
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Robin (or third type) boundary condition is a type of boundary condition, named after Victor Gustave Robin
Victor Gustave Robin
Victor Gustave Robin was a French mathematical analyst and applied mathematicianwho lectured in mathematical physics at the Sorbonne in Paris and also worked in the area of thermodynamics.. He is known especially for the Robin boundary condition....
(1855–1897). When imposed on an ordinary
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
or a partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
, it is a specification of a linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of the values of a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
and the values of its derivative on the boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
of the domain. Robin should be pronounced as a French
French language
French is a Romance language spoken as a first language in France, the Romandy region in Switzerland, Wallonia and Brussels in Belgium, Monaco, the regions of Quebec and Acadia in Canada, and by various communities elsewhere. Second-language speakers of French are distributed throughout many parts...
name (ʁoˈbɛ̃), although many English
English language
English is a West Germanic language that arose in the Anglo-Saxon kingdoms of England and spread into what was to become south-east Scotland under the influence of the Anglian medieval kingdom of Northumbria...
-speaking mathematicians anglicize the word (ˈrɔːbɪn).
Robin boundary conditions are a weighed combination of Dirichlet boundary condition
Dirichlet boundary condition
In mathematics, the Dirichlet boundary condition is a type of boundary condition, named after Johann Peter Gustav Lejeune Dirichlet who studied under Cauchy and succeeded Gauss at University of Göttingen. When imposed on an ordinary or a partial differential equation, it specifies the values a...
s and Neumann boundary condition
Neumann boundary condition
In mathematics, the Neumann boundary condition is a type of boundary condition, named after Carl Neumann.When imposed on an ordinary or a partial differential equation, it specifies the values that the derivative of a solution is to take on the boundary of the domain.* For an ordinary...
s. This contrasts to mixed boundary condition
Mixed boundary condition
In mathematics, a mixed boundary condition for a partial differential equation indicates that different boundary conditions are used on different parts of the boundary of the domain of the equation....
s, which are boundary conditions of different types specified on different subsets of the boundary. Robin boundary conditions are also called impedance boundary conditions, from their application in electromagnetic
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
problems.
If Ω is the domain on which the given equation is to be solved and
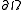 denotes its boundary
denotes its boundaryBoundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
, the Robin boundary condition is:
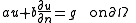
for some non-zero constants a and b and a given function g defined on
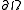 . Here, u is the unknown solution defined on
. Here, u is the unknown solution defined on  and
and 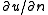 denotes the normal derivative at the boundary. More generally, a and b are allowed to be (given) functions, rather than constants.
denotes the normal derivative at the boundary. More generally, a and b are allowed to be (given) functions, rather than constants.In one dimension, if, for example,
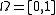 , the Robin boundary condition becomes the conditions:
, the Robin boundary condition becomes the conditions: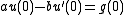
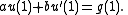
notice the change of sign in front of the term involving a derivative: that is because the normal to
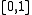 at 0 points in the negative direction, while at 1 it points in the positive direction.
at 0 points in the negative direction, while at 1 it points in the positive direction.Robin boundary conditions are commonly used in solving Sturm–Liouville problems which appear in many contexts in science and engineering.
In addition, the Robin boundary condition is a general form of the insulating boundary condition for convection–diffusion equation
Convection–diffusion equation
The convection–diffusion equation is a parabolic partial differential equation combining the diffusion equation and the advection equation, which describes...
s. Here, the convective and diffusive fluxes at the boundary sum to zero:
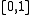
where D is the diffusive constant, u is the convective velocity at the boundary and c is the concentration. The first term is a result of Fick's law of diffusion
Fick's law of diffusion
Fick's laws of diffusion describe diffusion and can be used to solve for the diffusion coefficient, D. They were derived by Adolf Fick in the year 1855.- Fick's first law :...
.
See also
- Dirichlet boundary conditionDirichlet boundary conditionIn mathematics, the Dirichlet boundary condition is a type of boundary condition, named after Johann Peter Gustav Lejeune Dirichlet who studied under Cauchy and succeeded Gauss at University of Göttingen. When imposed on an ordinary or a partial differential equation, it specifies the values a...
- Neumann boundary conditionNeumann boundary conditionIn mathematics, the Neumann boundary condition is a type of boundary condition, named after Carl Neumann.When imposed on an ordinary or a partial differential equation, it specifies the values that the derivative of a solution is to take on the boundary of the domain.* For an ordinary...
- Mixed boundary conditionMixed boundary conditionIn mathematics, a mixed boundary condition for a partial differential equation indicates that different boundary conditions are used on different parts of the boundary of the domain of the equation....
- Cauchy boundary conditionCauchy boundary conditionIn mathematics, a Cauchy boundary condition imposed on an ordinary differential equation or a partial differential equation specifies both the values a solution of a differential equation is to take on the boundary of the domain and the normal derivative at the boundary. It corresponds to imposing...

