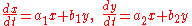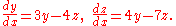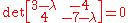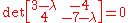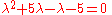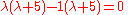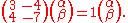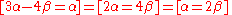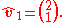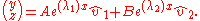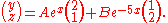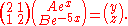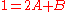Matrix differential equation
Encyclopedia
A differential equation
is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and of its derivatives of various orders. A matrix differential equation is one containing more than one function stacked into vector form with a matrix relating the functions to their derivatives.
For example, a simple matrix ordinary differential equation
is
where x(t) is an n×1 vector of functions of an underlying variable t, x'(t) is the vector of first derivatives of these functions, and A is an n×n matrix.
if and only if all eigenvalues of the matrix A have a negative real part. The steady state x* to which it converges if stable is found by setting x'(t)=0, yielding , assuming A is invertible. Thus the original equation can be written in homogeneous form in terms of deviations from the steady state:
, assuming A is invertible. Thus the original equation can be written in homogeneous form in terms of deviations from the steady state: 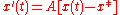 .
.
A different way of expressing this (closer to regular usage) is that x* is a particular solution to the in-homogenous equation, and all solutions will be on the form , with
, with 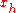 a solution to the homogenous equation (b=0).
a solution to the homogenous equation (b=0).
s can be used to express the solution of
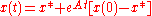 .
.
Putzer Algorithm for computing
Given a matrix  with eigenvalues
with eigenvalues  then
then
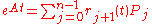
Where
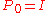
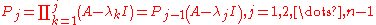
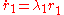

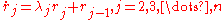

The equations for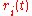 are simple first order nonhomogeneous ODEs.
are simple first order nonhomogeneous ODEs.
Notice the algorithm does not require that the matrix is diagonalizable
is diagonalizable
and avoids the complexity of using Jordan canonical form
when it is not needed.
where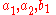 and
and 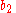 may be any arbitrary scalars.
may be any arbitrary scalars.
Higher order matrix ODE's may possess a much more complicated form.
The final, third, step in solving these sorts of ordinary differential equations is usually done by means of plugging in the values, calculated in the two previous steps into a specialized general form equation, which will be mentioned later in the article.
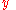 and function
and function  , both in terms of the single underlying variable x, in the following linear differential equation
, both in terms of the single underlying variable x, in the following linear differential equation
of the first order:
In order to solve this particular ordinary differential equation
, at some point of the solving process, we are going to need a so-called initial value, a starting point, which, in this particular case, we pick to be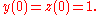
), mechanics
, physical mathematics, mathematical economics
, and linear algebra
.
Therefore, the process consists of the following:
The derivative
notation y' etc. seen in one of the vectors above is known as Lagrange's notation, first introduced by Joseph Louis Lagrange
. It is equivalent to the derivative notation dy/dx used in the previous equation, known as Leibniz's notation, honouring the name of Gottfried Leibniz
.
Once the coefficients of the two variables have been written in the matrix
form shown above, we may start the process of evaluating the eigenvalues. In order to do that we are going to have to find the determinant
of the matrix
that is formed when an identity matrix
,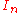 , multiplied by some constant lambda, symbol λ, is subtracted from our coefficient matrix in the following way:
, multiplied by some constant lambda, symbol λ, is subtracted from our coefficient matrix in the following way:
Applying further simplification and basic rules of matrix addition
we come up with the following:
Applying the rules of finding the determinant of a single 2×2 matrix, we obtain the following elementary quadratic equation
:
which may be reduced further to get a simpler version of the above:
Now finding the two roots,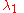 and
and  of the given quadratic equation
of the given quadratic equation
by applying the factorization
method we get the following:
The values, and
and 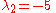 , that we have calculated above are the required eigenvalues. Once these two values are found, we may proceed to the second step of the solution process. The calculated eigenvalues will be used a little later in the final solution.
, that we have calculated above are the required eigenvalues. Once these two values are found, we may proceed to the second step of the solution process. The calculated eigenvalues will be used a little later in the final solution.
In some cases, say other matrix ODE's, the eigenvalues may be complex, in which case the following step of the solving process, as well as the final form and the solution, will be dramatically changed.
For each of the eigenvalues calculated we are going to have an individual eigenvector. For our first eigenvalue, which is , we have the following:
, we have the following:
Simplifying the above expression by applying basic matrix multiplication
rules we have:
All of these calculations have been done only to obtain the last expression, which in our case is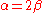 . Now taking some arbitrary value, presumably a small insignificant value, which is much easier to work with, for either
. Now taking some arbitrary value, presumably a small insignificant value, which is much easier to work with, for either  or
or 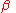 (in most cases it does not really matter), we substitute it into
(in most cases it does not really matter), we substitute it into 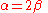 . Doing so will produce a very simple vector, which is the required eigenvector for this particular eigenvalue. In our case, we pick
. Doing so will produce a very simple vector, which is the required eigenvector for this particular eigenvalue. In our case, we pick  , which, in turn determines that
, which, in turn determines that  and, using the standard vector notation
and, using the standard vector notation
, our vector looks like this:
Performing the same operation using the second eigenvalue we calculated, which is , we obtain our second eigenvector. The process of working out this vector will not be shown but the final result is as follows:
, we obtain our second eigenvector. The process of working out this vector will not be shown but the final result is as follows:
Once both of the needed vectors have been found we may start our third and the last step. Do not forget that eigenvalues and eigenvectors that we have determined above will all be substituted into a specialized equation that will be shown shortly.
s that were given to us originally. There are two functions because our differential equations deal with two variables.
The equation, which involves all the pieces of information that we have previously found has the following form:
Substituting the values of eigenvalues and eigenvectors we get the following expression:
Applying further simplification rules we have:
Simplifying further and writing the equations for functions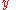 and
and  separately:
separately:
The above equations are in fact the functions that we needed to find, but they are in their general form and if we want to actually find their exact forms and solutions, now is the time to look back at the information given to us, the so-called initial value problem
. At some point during solving these equations we have come across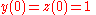 , which plays the role of starting point for our ordinary differential equation. Now is the time to apply this condition. As a result of application of this condition we will be able to find the constants, A and B. As we see from the
, which plays the role of starting point for our ordinary differential equation. Now is the time to apply this condition. As a result of application of this condition we will be able to find the constants, A and B. As we see from the 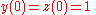 condition, when
condition, when  , the overall equation is equal to 1. Thus we may construct the following system of linear equations:
, the overall equation is equal to 1. Thus we may construct the following system of linear equations:
Solving these equations we find that both constants A and B are equal to 1/3. Therefore if we substitute these values into the general form of these two functions we will have their exact forms:
which is our final form of the two functions we were required to find.
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and of its derivatives of various orders. A matrix differential equation is one containing more than one function stacked into vector form with a matrix relating the functions to their derivatives.
For example, a simple matrix ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
is
- x'(t) = Ax(t),
where x(t) is an n×1 vector of functions of an underlying variable t, x'(t) is the vector of first derivatives of these functions, and A is an n×n matrix.
Stability and steady state of the matrix system
The matrix equation x'(t) = Ax(t) + b with n×1 parameter vector b is stableStability theory
In mathematics, stability theory addresses the stability of solutions of differential equations and of trajectories of dynamical systems under small perturbations of initial conditions...
if and only if all eigenvalues of the matrix A have a negative real part. The steady state x* to which it converges if stable is found by setting x'(t)=0, yielding
 , assuming A is invertible. Thus the original equation can be written in homogeneous form in terms of deviations from the steady state:
, assuming A is invertible. Thus the original equation can be written in homogeneous form in terms of deviations from the steady state: 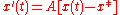 .
.A different way of expressing this (closer to regular usage) is that x* is a particular solution to the in-homogenous equation, and all solutions will be on the form
 , with
, with 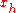 a solution to the homogenous equation (b=0).
a solution to the homogenous equation (b=0).Solution in matrix form
Matrix exponentialMatrix exponential
In mathematics, the matrix exponential is a matrix function on square matrices analogous to the ordinary exponential function. Abstractly, the matrix exponential gives the connection between a matrix Lie algebra and the corresponding Lie group....
s can be used to express the solution of

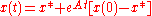 .
.Putzer Algorithm for computing 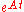
Given a matrix  with eigenvalues
with eigenvalues  then
then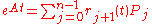
Where
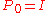
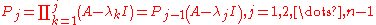
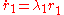

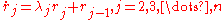

The equations for
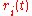 are simple first order nonhomogeneous ODEs.
are simple first order nonhomogeneous ODEs.Notice the algorithm does not require that the matrix
 is diagonalizable
is diagonalizableDiagonalizable matrix
In linear algebra, a square matrix A is called diagonalizable if it is similar to a diagonal matrix, i.e., if there exists an invertible matrix P such that P −1AP is a diagonal matrix...
and avoids the complexity of using Jordan canonical form
Jordan normal form
In linear algebra, a Jordan normal form of a linear operator on a finite-dimensional vector space is an upper triangular matrix of a particular form called Jordan matrix, representing the operator on some basis...
when it is not needed.
Deconstructed example of a matrix ordinary differential equation
A first-order homogeneous matrix ordinary differential equation in two functions x(t) and y(t), when taken out of matrix form, has the following form:where
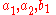 and
and 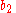 may be any arbitrary scalars.
may be any arbitrary scalars.Higher order matrix ODE's may possess a much more complicated form.
Solving deconstructed matrix ordinary differential equations
The process of solving the above equations and finding the required functions, of this particular order and form, consists of 3 main steps. Brief descriptions of each of these steps are listed below:- Finding the eigenvalues
- Finding the eigenvectors
- Finding the needed functions
The final, third, step in solving these sorts of ordinary differential equations is usually done by means of plugging in the values, calculated in the two previous steps into a specialized general form equation, which will be mentioned later in the article.
Solved example of a matrix ODE
In order to show how the matrix ODE's may actually be solved according to the 3 above steps, by means of using simple matrices in the process, let us find, say function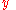 and function
and function  , both in terms of the single underlying variable x, in the following linear differential equation
, both in terms of the single underlying variable x, in the following linear differential equationLinear differential equation
Linear differential equations are of the formwhere the differential operator L is a linear operator, y is the unknown function , and the right hand side ƒ is a given function of the same nature as y...
of the first order:
In order to solve this particular ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
, at some point of the solving process, we are going to need a so-called initial value, a starting point, which, in this particular case, we pick to be
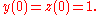
First step
The first step, that has already been mentioned above, is finding the eigenvalues. The process of finding the eigenvalues is not a very difficult process. Both eigenvalues and eigenvectors are found to be useful in numerous branches of mathematics, including higher engineering mathematics/calculations(i.e. Applied MathematicsApplied mathematics
Applied mathematics is a branch of mathematics that concerns itself with mathematical methods that are typically used in science, engineering, business, and industry. Thus, "applied mathematics" is a mathematical science with specialized knowledge...
), mechanics
Mechanics
Mechanics is the branch of physics concerned with the behavior of physical bodies when subjected to forces or displacements, and the subsequent effects of the bodies on their environment....
, physical mathematics, mathematical economics
Mathematical economics
Mathematical economics is the application of mathematical methods to represent economic theories and analyze problems posed in economics. It allows formulation and derivation of key relationships in a theory with clarity, generality, rigor, and simplicity...
, and linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
.
Therefore, the process consists of the following:
-
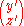 =
= 
The derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
notation y' etc. seen in one of the vectors above is known as Lagrange's notation, first introduced by Joseph Louis Lagrange
Joseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
. It is equivalent to the derivative notation dy/dx used in the previous equation, known as Leibniz's notation, honouring the name of Gottfried Leibniz
Gottfried Leibniz
Gottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
.
Once the coefficients of the two variables have been written in the matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
form shown above, we may start the process of evaluating the eigenvalues. In order to do that we are going to have to find the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
that is formed when an identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
,
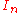 , multiplied by some constant lambda, symbol λ, is subtracted from our coefficient matrix in the following way:
, multiplied by some constant lambda, symbol λ, is subtracted from our coefficient matrix in the following way:-
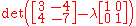 .
.
Applying further simplification and basic rules of matrix addition
Matrix addition
In mathematics, matrix addition is the operation of adding two matrices by adding the corresponding entries together. However, there are other operations which could also be considered as a kind of addition for matrices, the direct sum and the Kronecker sum....
we come up with the following:
-
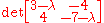 .
.
Applying the rules of finding the determinant of a single 2×2 matrix, we obtain the following elementary quadratic equation
Quadratic equation
In mathematics, a quadratic equation is a univariate polynomial equation of the second degree. A general quadratic equation can be written in the formax^2+bx+c=0,\,...
:
which may be reduced further to get a simpler version of the above:
-
 .
.
Now finding the two roots,
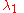 and
and  of the given quadratic equation
of the given quadratic equationQuadratic equation
In mathematics, a quadratic equation is a univariate polynomial equation of the second degree. A general quadratic equation can be written in the formax^2+bx+c=0,\,...
by applying the factorization
Factorization
In mathematics, factorization or factoring is the decomposition of an object into a product of other objects, or factors, which when multiplied together give the original...
method we get the following:
-
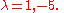 .
.
The values,
 and
and 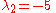 , that we have calculated above are the required eigenvalues. Once these two values are found, we may proceed to the second step of the solution process. The calculated eigenvalues will be used a little later in the final solution.
, that we have calculated above are the required eigenvalues. Once these two values are found, we may proceed to the second step of the solution process. The calculated eigenvalues will be used a little later in the final solution.In some cases, say other matrix ODE's, the eigenvalues may be complex, in which case the following step of the solving process, as well as the final form and the solution, will be dramatically changed.
Second step
As it was already mentioned above, in a simple description, this step involves finding the eigenvectors by means of using the information originally given to us.For each of the eigenvalues calculated we are going to have an individual eigenvector. For our first eigenvalue, which is
 , we have the following:
, we have the following:Simplifying the above expression by applying basic matrix multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
rules we have:
-
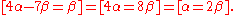 .
.
All of these calculations have been done only to obtain the last expression, which in our case is
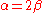 . Now taking some arbitrary value, presumably a small insignificant value, which is much easier to work with, for either
. Now taking some arbitrary value, presumably a small insignificant value, which is much easier to work with, for either  or
or 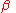 (in most cases it does not really matter), we substitute it into
(in most cases it does not really matter), we substitute it into 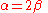 . Doing so will produce a very simple vector, which is the required eigenvector for this particular eigenvalue. In our case, we pick
. Doing so will produce a very simple vector, which is the required eigenvector for this particular eigenvalue. In our case, we pick  , which, in turn determines that
, which, in turn determines that  and, using the standard vector notation
and, using the standard vector notationVector notation
This page is an overview of the common notations used when working with vectors, which may be spatial or more abstract members of vector spaces....
, our vector looks like this:
Performing the same operation using the second eigenvalue we calculated, which is
 , we obtain our second eigenvector. The process of working out this vector will not be shown but the final result is as follows:
, we obtain our second eigenvector. The process of working out this vector will not be shown but the final result is as follows:Once both of the needed vectors have been found we may start our third and the last step. Do not forget that eigenvalues and eigenvectors that we have determined above will all be substituted into a specialized equation that will be shown shortly.
Third (final) step
The purpose of this final step is to actually find the required functions, that are 'hidden' behind the derivativeDerivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s that were given to us originally. There are two functions because our differential equations deal with two variables.
The equation, which involves all the pieces of information that we have previously found has the following form:
Substituting the values of eigenvalues and eigenvectors we get the following expression:
Applying further simplification rules we have:
Simplifying further and writing the equations for functions
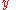 and
and  separately:
separately:The above equations are in fact the functions that we needed to find, but they are in their general form and if we want to actually find their exact forms and solutions, now is the time to look back at the information given to us, the so-called initial value problem
Initial value problem
In mathematics, in the field of differential equations, an initial value problem is an ordinary differential equation together with a specified value, called the initial condition, of the unknown function at a given point in the domain of the solution...
. At some point during solving these equations we have come across
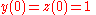 , which plays the role of starting point for our ordinary differential equation. Now is the time to apply this condition. As a result of application of this condition we will be able to find the constants, A and B. As we see from the
, which plays the role of starting point for our ordinary differential equation. Now is the time to apply this condition. As a result of application of this condition we will be able to find the constants, A and B. As we see from the 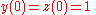 condition, when
condition, when  , the overall equation is equal to 1. Thus we may construct the following system of linear equations:
, the overall equation is equal to 1. Thus we may construct the following system of linear equations:Solving these equations we find that both constants A and B are equal to 1/3. Therefore if we substitute these values into the general form of these two functions we will have their exact forms:
which is our final form of the two functions we were required to find.
See also
- Nonhomogeneous equations
- Matrix difference equationMatrix difference equationA matrix difference equation is a difference equation in which the value of a vector of variables at one point in time is related to its own value at one or more previous points in time, using matrices. Occasionally, the time-varying entity may itself be a matrix instead of a vector...
- Newton's law of cooling
- Fibonacci Sequence
- Difference equations
- Wave equationWave equationThe wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...