Split-step method
Encyclopedia
In numerical analysis
, the split-step (Fourier) method is a pseudo-spectral
numerical method used to solve nonlinear partial differential equation
s like the nonlinear Schrödinger equation
. The name arises for two reasons. First, the method relies on computing the solution in small steps, and treating the linear and the nonlinear steps separately (see below). Second, it is necessary to Fourier transform
back and forth because the linear step is made in the frequency domain
while the nonlinear step is made in the time domain
.
An example of usage of this method is in the field of light pulse propagation in optical fibers, where the interaction of linear and nonlinear mechanisms makes it difficult to find general analytical solutions. However, the split-step method provides a numerical solution to the problem.
where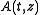
describes the pulse envelope in time 
at the spatial position 
. The equation can be split into a linear part,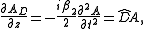
and a nonlinear part,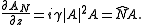
Both the linear and the nonlinear parts have analytical solutions, but the nonlinear Schrödinger equation
containing both parts does not have a general analytical solution.
However, if only a 'small' step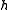
is taken along 
, then the two parts can be treated separately with only a 'small' numerical error. One can therefore first take a small nonlinear step,
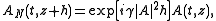
using the analytical solution.
The dispersion step has an analytical solution in the frequency domain
, so it is first necessary to Fourier transform
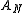using
,
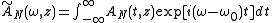where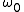
is the center frequency of the pulse.
It can be shown that using the above definition of the Fourier transform
, the analytical solution to the linear step, commuted with the frequency domain solution for the nonlinear step, is
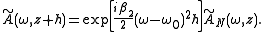
By taking the inverse Fourier transform of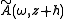
one obtains 
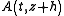; the pulse has thus been propagated a small step 
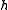. By repeating the above 
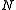times, the pulse can be propagated over a length of 
.
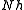The above shows how to use the method to propagate a solution forward in space; however, many physics applications, such as studying the evolution of a wave packet describing a particle, require one to propagate the solution forward in time rather than in space. The non-linear Schrödinger equation, when used to govern the time evolution of a wave function, takes the form
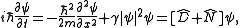
where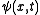
describes the wave function at position 
and time 
. Note that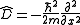
and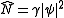 
, and that 
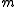is the mass of the particle and 
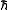is Planck's constant over 
.
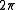The formal solution to this equation is a complex exponential, so we have that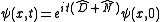
.
Since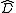
and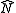 
are operators, they do not in general commute. However, the Baker-Hausdorff formula can be applied to show that the error from treating them as if they do will be of order 
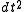if we are taking a small but finite time step 
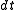. We therefore can write
.
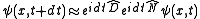The part of this equation involving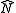
can be computed directly using the wave function at time 
, but to compute the exponential involving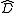 
we use the fact that in frequency space, the partial derivative operator can be converted into a number by substituting 
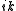for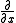 
, where 
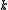is the frequency (or more properly, wave number, as we are dealing with a spatial variable and thus transforming to a space of spatial frequencies—i.e. wave numbers) associated with the Fourier transform of whatever is being operated on. Thus, we take the Fourier transform of
,
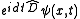recover the associated wave number, compute the quantity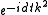
,
and use it to find the product of the complex exponentials involving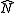
and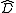 
in frequency space as below:
,
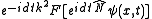where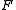
denotes a Fourier transform. We then inverse Fourier transform this expression to find the final result in physical space, yielding the final expression
.
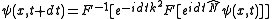A variation on this method is the symmetrized split-step Fourier method, which takes half a time step using one operator, then takes a full time step with only the other, and then takes a second half time step again with only the first. This method is an improvement upon the generic split-step Fourier method because its error is of order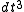
for a time step 
.
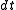The Fourier transform
s of this algorithm
can be computed relatively fast using the fast Fourier transform (FFT)
. The split-step Fourier method can therefore be much faster than typical finite difference method
s.
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, the split-step (Fourier) method is a pseudo-spectral
Pseudo-spectral method
Pseudo-spectral methods are a class of numerical methods used in applied mathematics and scientific computing for the solution of PDEs, such as the direct simulation of a particle with an arbitrary wavefunction interacting with an arbitrary potential...
numerical method used to solve nonlinear partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s like the nonlinear Schrödinger equation
Nonlinear Schrödinger equation
In theoretical physics, the nonlinear Schrödinger equation is a nonlinear version of Schrödinger's equation. It is a classical field equation with applications to optics and water waves. Unlike the Schrödinger equation, it never describes the time evolution of a quantum state...
. The name arises for two reasons. First, the method relies on computing the solution in small steps, and treating the linear and the nonlinear steps separately (see below). Second, it is necessary to Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
back and forth because the linear step is made in the frequency domain
Frequency domain
In electronics, control systems engineering, and statistics, frequency domain is a term used to describe the domain for analysis of mathematical functions or signals with respect to frequency, rather than time....
while the nonlinear step is made in the time domain
Time domain
Time domain is a term used to describe the analysis of mathematical functions, physical signals or time series of economic or environmental data, with respect to time. In the time domain, the signal or function's value is known for all real numbers, for the case of continuous time, or at various...
.
An example of usage of this method is in the field of light pulse propagation in optical fibers, where the interaction of linear and nonlinear mechanisms makes it difficult to find general analytical solutions. However, the split-step method provides a numerical solution to the problem.
Description of the method
Consider, for example, the nonlinear Schrödinger equationNonlinear Schrödinger equation
In theoretical physics, the nonlinear Schrödinger equation is a nonlinear version of Schrödinger's equation. It is a classical field equation with applications to optics and water waves. Unlike the Schrödinger equation, it never describes the time evolution of a quantum state...
where
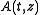describes the pulse envelope in time at the spatial position . The equation can be split into a linear part,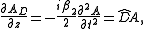and a nonlinear part,
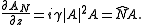
Both the linear and the nonlinear parts have analytical solutions, but the nonlinear Schrödinger equation
Nonlinear Schrödinger equation
In theoretical physics, the nonlinear Schrödinger equation is a nonlinear version of Schrödinger's equation. It is a classical field equation with applications to optics and water waves. Unlike the Schrödinger equation, it never describes the time evolution of a quantum state...
containing both parts does not have a general analytical solution.
However, if only a 'small' step
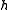is taken along , then the two parts can be treated separately with only a 'small' numerical error. One can therefore first take a small nonlinear step,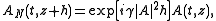using the analytical solution.
The dispersion step has an analytical solution in the frequency domain
Frequency domain
In electronics, control systems engineering, and statistics, frequency domain is a term used to describe the domain for analysis of mathematical functions or signals with respect to frequency, rather than time....
, so it is first necessary to Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
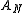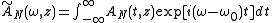using,where
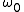is the center frequency of the pulse.It can be shown that using the above definition of the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
, the analytical solution to the linear step, commuted with the frequency domain solution for the nonlinear step, is
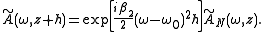
By taking the inverse Fourier transform of
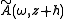one obtains 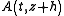; the pulse has thus been propagated a small step 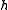. By repeating the above 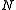times, the pulse can be propagated over a length of 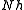.The above shows how to use the method to propagate a solution forward in space; however, many physics applications, such as studying the evolution of a wave packet describing a particle, require one to propagate the solution forward in time rather than in space. The non-linear Schrödinger equation, when used to govern the time evolution of a wave function, takes the form
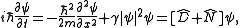
where
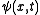describes the wave function at position and time . Note that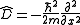 and 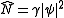, and that 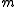is the mass of the particle and 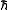is Planck's constant over 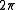.The formal solution to this equation is a complex exponential, so we have that
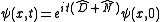.Since
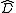and 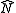are operators, they do not in general commute. However, the Baker-Hausdorff formula can be applied to show that the error from treating them as if they do will be of order 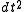if we are taking a small but finite time step 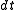. We therefore can write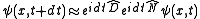.The part of this equation involving
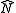can be computed directly using the wave function at time , but to compute the exponential involving 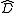we use the fact that in frequency space, the partial derivative operator can be converted into a number by substituting 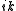for 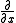, where 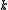is the frequency (or more properly, wave number, as we are dealing with a spatial variable and thus transforming to a space of spatial frequencies—i.e. wave numbers) associated with the Fourier transform of whatever is being operated on. Thus, we take the Fourier transform of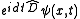,recover the associated wave number, compute the quantity
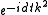,and use it to find the product of the complex exponentials involving
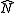and 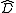in frequency space as below: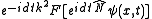,where
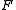denotes a Fourier transform. We then inverse Fourier transform this expression to find the final result in physical space, yielding the final expression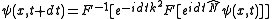.A variation on this method is the symmetrized split-step Fourier method, which takes half a time step using one operator, then takes a full time step with only the other, and then takes a second half time step again with only the first. This method is an improvement upon the generic split-step Fourier method because its error is of order
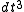for a time step 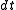.The Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
s of this algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
can be computed relatively fast using the fast Fourier transform (FFT)
Fast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
. The split-step Fourier method can therefore be much faster than typical finite difference method
Finite difference method
In mathematics, finite-difference methods are numerical methods for approximating the solutions to differential equations using finite difference equations to approximate derivatives.- Derivation from Taylor's polynomial :...
s.
External references
- Thomas E. Murphy, Software, http://www.photonics.umd.edu/software/ssprop/
- Andrés A. Rieznik, Software, http://photonics.incubadora.fapesp.br
- Prof. G. Agrawal, Software, http://www.optics.rochester.edu/workgroups/agrawal/grouphomepage.php?pageid=software
- Thomas Schreiber, Software, http://www.fiberdesk.com
- Edward J. Grace, Software, http://www.mathworks.com/matlabcentral/fileexchange/24016