Spectral element method
Encyclopedia
In mathematics
, the spectral element method is a high order finite element method
.
Introduced in a 1984 paper by A. T. Patera, the abstract begins: "A spectral element method that combines the generality of the finite element method with the accuracy of spectral techniques..."
The spectral element method is an elegant formulation of the finite element method
with a high degree piecewise polynomial basis.
expands the solution in trigonometric series, a chief advantage is that the resulting method is of very high order. This approach relies on the fact that trigonometric polynomials are an orthonormal basis
for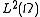
. The spectral element method chooses instead high degree piecewise polynomial basis functions, also achieving a very high order of accuracy.
holds here and it can be shown that, if u is the solution of the weak equation, uN is the approximate solution and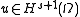
:
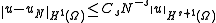
where C is independent from N and s is no larger than the degree of the piecewise polynomial basis. As we increase N, we can also increase the degree of the basis functions. In this case, if u is an analytic function
:
where
depends only on 
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the spectral element method is a high order finite element method
Finite element method
The finite element method is a numerical technique for finding approximate solutions of partial differential equations as well as integral equations...
.
Introduced in a 1984 paper by A. T. Patera, the abstract begins: "A spectral element method that combines the generality of the finite element method with the accuracy of spectral techniques..."
The spectral element method is an elegant formulation of the finite element method
Finite element method
The finite element method is a numerical technique for finding approximate solutions of partial differential equations as well as integral equations...
with a high degree piecewise polynomial basis.
Discussion
The spectral methodSpectral method
Spectral methods are a class of techniques used in applied mathematics and scientific computing to numerically solve certain Dynamical Systems, often involving the use of the Fast Fourier Transform. Where applicable, spectral methods have excellent error properties, with the so called "exponential...
expands the solution in trigonometric series, a chief advantage is that the resulting method is of very high order. This approach relies on the fact that trigonometric polynomials are an orthonormal basis
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
for
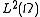. The spectral element method chooses instead high degree piecewise polynomial basis functions, also achieving a very high order of accuracy.A-priori error estimate
The classic analysis of Galerkin methods and Céa's lemmaCéa's lemma
Céa's lemma is a lemma in mathematics. It is an important tool for proving error estimates for the finite element method applied to elliptic partial differential equations.-Lemma statement:Let V be a real Hilbert space with the norm \|\cdot\|...
holds here and it can be shown that, if u is the solution of the weak equation, uN is the approximate solution and
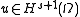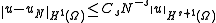
:where C is independent from N and s is no larger than the degree of the piecewise polynomial basis. As we increase N, we can also increase the degree of the basis functions. In this case, if u is an analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
:
where
depends only on .Related methods
- G-NI or SEM-NI: these are the most used spectral methods. The Galerkin formulation of spectral methods or spectral element methods, for G-NI or SEM-NI respectively, is modified and Gaussian numerical integration is used instead of integrals in the definition of the bilinear form
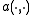and in the functional 
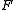. These method are a family of Petrov–Galerkin methods their convergence is a consequence of Strang's lemma. - The spectral element method uses tensor product space spanned by nodal basis functions associated with Gauss–Lobatto points. In contrast, the p-version finite element methodHp-FEMhp-FEM is a general version of the finite element method , a numerical method for solving partial differential equations based on piecewise-polynomial approximations that employs elements of variable size and polynomial degree ...
spans a space of high order polynomials by nodeless basis functions, chosen approximately orthogonal for numerical stability. Since not all interior basis functions need to be present, the p-version finite element method can create a space that contains all polynomials up to a given degree with many fewer degrees of freedom. However, some speedup techniques possible in spectral methods due to their tensor-product character are no longer available. The name p-version means that accuracy is increased by increasing the order of the approximating polynomials (thus, p) rather than decreasing the mesh size, h. - The hp finite element method (hp-FEMHp-FEMhp-FEM is a general version of the finite element method , a numerical method for solving partial differential equations based on piecewise-polynomial approximations that employs elements of variable size and polynomial degree ...
) combines the advantages of the h and p refinements to obtain extremely fast, exponential convergence rates.