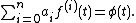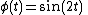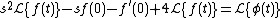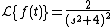Laplace transform applied to differential equations

The use of Laplace transform makes it much easier to solve linear differential equations

Ordinary differential equation

In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....

with given initial conditions.

First consider the following relations:

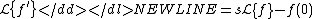
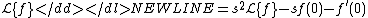
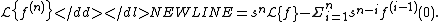
Consider the following differential equation:

This equation is equivalent to

which is equivalent to

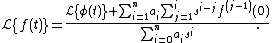
Note that the

are initial conditions.

The solution for f(t) will be given by applying the Laplace inverse transform to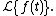

An example
We want to solve

with initial conditions f(0) = 0 and f ′(0)=0.

We note that

and we get

So this is equivalent to

We deduce

So we apply the Laplace inverse transform and get

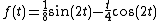
The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.