
Dual representation
Encyclopedia
In mathematics
, if G is a group
and ρ is a linear representation of it on the vector space
V, then the dual representation is defined over the dual vector space as follows:
for all g in G. Then is also a representation, as may be checked explicitly. The dual representation is also known as the contragredient representation.
If is a Lie algebra
is a Lie algebra
and ρ is a representation of it over the vector space V, then the dual representation is defined over the dual vector space as follows:
For a unitary representation
, the conjugate representation and the dual representation coincide, up to equivalence of representations.
does not admit a dual representation. Modules of Hopf algebra
s do, however.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, if G is a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
and ρ is a linear representation of it on the vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V, then the dual representation is defined over the dual vector space as follows:
- (g) is the transpose of ρ(g−1)
for all g in G. Then is also a representation, as may be checked explicitly. The dual representation is also known as the contragredient representation.
If
 is a Lie algebra
is a Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
and ρ is a representation of it over the vector space V, then the dual representation is defined over the dual vector space as follows:
- (u) is the transpose of −ρ(u) for all u in
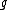 .
.
- is also a representation, as you may check explicitly.
For a unitary representation
Unitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
, the conjugate representation and the dual representation coincide, up to equivalence of representations.
Generalization
A general ring moduleModule (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
does not admit a dual representation. Modules of Hopf algebra
Hopf algebra
In mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property.Hopf algebras occur naturally...
s do, however.

