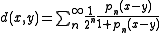Locally convex topological vector space
Encyclopedia
In functional analysis
and related areas of mathematics
, locally convex topological vector spaces or locally convex spaces are examples of topological vector space
s (TVS) which generalize normed spaces. They can be defined as topological
vector spaces whose topology is generated
by translations of balanced
, absorbent, convex set
s. Alternatively they can be defined as a vector space with a family
of seminorms, and a topology can be defined in terms of that family. Although in general such spaces are not necessarily normable, the existence of a convex local base for the zero vector is strong enough for the Hahn–Banach theorem
to hold, yielding a sufficiently rich theory of continuous linear functional
s.
Fréchet spaces are locally convex spaces which are metrizable and complete
with respect to this metric
. They are generalizations of Banach spaces, which are complete vector spaces with respect to a norm
.
of the complex numbers (normally C itself or R). A locally convex space is defined either in terms of convex sets, or equivalently in terms of seminorms.
A locally convex topological vector space is a topological vector space
in which the origin has a local base of absolutely convex absorbent sets. Because translation is (by definition of "topological vector space") continuous, all translations are homeomorphisms, so every base for the neighborhoods of the origin can be translated to a base for the neighborhoods of any given vector.
If p satisfies positive definiteness, which states that if p(x) = 0 then x = 0, then p is a norm. While in general seminorms need not be norms, there is an analogue of this criterion for families of seminorms, separatedness, defined below.
A locally convex space is then defined to be a vector space V along with a family
of seminorms {pα}α ∈ A on V. The space carries a natural topology, the initial topology
of the seminorms. In other words, it is the coarsest
topology for which all mappings x → pα(x−x0), x0 ∈ V, α ∈ A, are continuous. A base of neighborhoods of x0 for this topology is obtained in the following way: for every finite subset B of A and every ε > 0, let
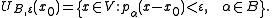
That the vector space operations are continuous in this topology follows from properties 2 and 3 above. The resulting TVS is locally convex because each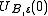
is absolutely convex and absorbent.
or Minkowski gauge. The key feature of seminorms which ensures the convexity of their ε-ball
s is the triangle inequality
.
For an absorbing set C such that if x is in C, then tx is in C whenever 0 ≤ t ≤ 1, define the Minkowski functional of C to be
From this definition it follows that μC is a seminorm if C is balanced and convex (it is also absorbent by assumption). Conversely, given a family of seminorms, the sets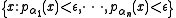
form a base of convex absorbent balanced sets.
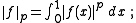
they are not locally convex, since the only convex neighborhood of zero is the whole space. More generally the spaces Lp(μ) with an atomless, finite measure μ and 0 < p < 1 are not locally convex.
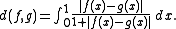
Both examples have the property that any continuous linear map to the real numbers is 0. In particular, their dual space
is trivial, that is, it contains only the zero functional.
found for Banach spaces.
Given locally convex spaces V and W with families of seminorms {pα}α and {qβ}β respectively, a linear map T from V to W is continuous if and only if for every β there exist α1, α2, ... , αn and exists an M>0 such that for all x in X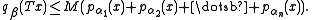
In other words, each seminorm of the range of T is bounded
above by some finite sum of seminorms in the domain. If the family {pα}α is a directed family, and it can always be chosen to be directed as explained above, then the formula becomes even simpler and more familiar: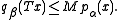
The class
of all locally convex topological vector spaces forms a category
with continuous linear maps as morphism
s.
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
and related areas of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, locally convex topological vector spaces or locally convex spaces are examples of topological vector space
Topological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
s (TVS) which generalize normed spaces. They can be defined as topological
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
vector spaces whose topology is generated
Base (topology)
In mathematics, a base B for a topological space X with topology T is a collection of open sets in T such that every open set in T can be written as a union of elements of B. We say that the base generates the topology T...
by translations of balanced
Balanced set
In linear algebra and related areas of mathematics a balanced set, circled set or disk in a vector space is a set S so that for all scalars α with |α| ≤ 1\alpha S \subseteq S...
, absorbent, convex set
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
s. Alternatively they can be defined as a vector space with a family
Family of sets
In set theory and related branches of mathematics, a collection F of subsets of a given set S is called a family of subsets of S, or a family of sets over S. More generally, a collection of any sets whatsoever is called a family of sets...
of seminorms, and a topology can be defined in terms of that family. Although in general such spaces are not necessarily normable, the existence of a convex local base for the zero vector is strong enough for the Hahn–Banach theorem
Hahn–Banach theorem
In mathematics, the Hahn–Banach theorem is a central tool in functional analysis. It allows the extension of bounded linear functionals defined on a subspace of some vector space to the whole space, and it also shows that there are "enough" continuous linear functionals defined on every normed...
to hold, yielding a sufficiently rich theory of continuous linear functional
Linear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
s.
Fréchet spaces are locally convex spaces which are metrizable and complete
Complete space
In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
with respect to this metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
. They are generalizations of Banach spaces, which are complete vector spaces with respect to a norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
.
Definition
Suppose V is a vector space over K, a subfieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
of the complex numbers (normally C itself or R). A locally convex space is defined either in terms of convex sets, or equivalently in terms of seminorms.
Convex sets
A subset C in V is called- ConvexConvex setIn Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
if for each x and y in C, tx+(1–t)y is in C for all t in the unit intervalUnit intervalIn mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
, that is whenever 0 ≤ t ≤ 1. In other words, C contains all line segments between points in C. - Circled if for all x in C, λx is in C if |λ|=1. If the underlying field K is the real numbers, this means that C is equal to its reflection through the origin. For a complex vector space V, it means for any x in C, C contains the circle through x, centred on the origin, in the one-dimensional complex subspace generated by x.
- A coneCone (linear algebra)In linear algebra, a cone is a subset of a vector space that is closed under multiplication by positive scalars. In other words, a subset C of a real vector space V is a cone if and only if λx belongs to C for any x in C and any positive scalar λ of V .A cone is said...
(when the underlying field is ordered) if for every x in C and 0 ≤ λ ≤ 1, λx is in C. - BalancedBalanced setIn linear algebra and related areas of mathematics a balanced set, circled set or disk in a vector space is a set S so that for all scalars α with |α| ≤ 1\alpha S \subseteq S...
if for all x in C, λx is in C if |λ| ≤ 1. If the underlying field K is the real numbers, this means that if x is in C, C contains the line segment between x and -x. For a complex vector space V, it means for any x in C, C contains the disk with x on its boundary, centred on the origin, in the one-dimensional complex subspace generated by x. Equivalently, a balanced set is a circled cone. - Absorbent or absorbing if the union of tC over all t > 0 is all of V, or equivalently for every x in V, tx is in C for some t > 0. The set C can be scaled out to absorb every point in the space.
- Absolutely convex if it is both balanced and convex.
A locally convex topological vector space is a topological vector space
Topological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
in which the origin has a local base of absolutely convex absorbent sets. Because translation is (by definition of "topological vector space") continuous, all translations are homeomorphisms, so every base for the neighborhoods of the origin can be translated to a base for the neighborhoods of any given vector.
Seminorms
A seminorm on V is a map p : V → R such that- p is positive or positive semidefinite: p(x) ≥ 0.
- p is positive homogeneous or positive scalable: p(λx) = |λ| p(x) for every scalar λ. So, in particular, p(0) = 0.
- p is subadditive. It satisfies the triangle inequality: p(x + y) ≤ p(x) + p(y).
If p satisfies positive definiteness, which states that if p(x) = 0 then x = 0, then p is a norm. While in general seminorms need not be norms, there is an analogue of this criterion for families of seminorms, separatedness, defined below.
A locally convex space is then defined to be a vector space V along with a family
Family of sets
In set theory and related branches of mathematics, a collection F of subsets of a given set S is called a family of subsets of S, or a family of sets over S. More generally, a collection of any sets whatsoever is called a family of sets...
of seminorms {pα}α ∈ A on V. The space carries a natural topology, the initial topology
Initial topology
In general topology and related areas of mathematics, the initial topology on a set X, with respect to a family of functions on X, is the coarsest topology on X which makes those functions continuous.The subspace topology and product topology constructions are both special cases of initial...
of the seminorms. In other words, it is the coarsest
Comparison of topologies
In topology and related areas of mathematics comparison of topologies refers to the fact that two topological structures on a given set may stand in relation to each other. The set of all possible topologies on a given set forms a partially ordered set...
topology for which all mappings x → pα(x−x0), x0 ∈ V, α ∈ A, are continuous. A base of neighborhoods of x0 for this topology is obtained in the following way: for every finite subset B of A and every ε > 0, let
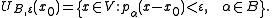
That the vector space operations are continuous in this topology follows from properties 2 and 3 above. The resulting TVS is locally convex because each
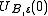is absolutely convex and absorbent.Equivalence of definitions
Although the definition in terms of a neighborhood base gives a better geometric picture, the definition in terms of seminorms is easier to work with in practice. The equivalence of the two definitions follows from a construction known as the Minkowski functionalMinkowski functional
In functional analysis, given a linear space X, a Minkowski functional is a device that uses the linear structure to introduce a topology on X.-Example 1:...
or Minkowski gauge. The key feature of seminorms which ensures the convexity of their ε-ball
Ball (mathematics)
In mathematics, a ball is the space inside a sphere. It may be a closed ball or an open ball ....
s is the triangle inequality
Triangle inequality
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
.
For an absorbing set C such that if x is in C, then tx is in C whenever 0 ≤ t ≤ 1, define the Minkowski functional of C to be
From this definition it follows that μC is a seminorm if C is balanced and convex (it is also absorbent by assumption). Conversely, given a family of seminorms, the sets
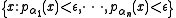
form a base of convex absorbent balanced sets.
Further definitions and properties
- A family of seminorms {pα}α is called total or separated or is said to separate points if whenever pα(x) = 0 holds for every α then x is necessarily 0. A locally convex space is HausdorffHausdorff spaceIn topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
it has a separated family of seminorms. Many authors take the Hausdorff criterion in the definition. - A pseudometricPseudometric spaceIn mathematics, a pseudometric space is a generalized metric space in which the distance between two distinct points can be zero. In the same way as every normed space is a metric space, every seminormed space is a pseudometric space...
is a generalisation of a metric which does not satisfy the condition that d(x,y) = 0 only when x = y. A locally convex space is pseudometrisable, meaning that its topology arises from a pseudometric, if and only if it has a countable family of seminorms. Indeed, a pseudometric inducing the same topology is then given by
(where the 1/2n can be replaced by any positive summable sequence an).
This pseudometric is translation-invariant, but not homogeneous, meaning d(kx,ky) does not equal |k|d(x,y), and therefore does not
define a (pseudo)norm.
The pseudometric is an honest metric if and only if the family of seminorms is separated,
since this is the case if and only if the space is Hausdorff.
If furthermore the space is complete, the space is called a Fréchet spaceFréchet spaceIn functional analysis and related areas of mathematics, Fréchet spaces, named after Maurice Fréchet, are special topological vector spaces. They are generalizations of Banach spaces...
.
-
- As with any topological vector space, a locally convex space is also a uniform spaceUniform spaceIn the mathematical field of topology, a uniform space is a set with a uniform structure. Uniform spaces are topological spaces with additional structure which is used to define uniform properties such as completeness, uniform continuity and uniform convergence.The conceptual difference between...
. Thus one may speak of uniform continuityUniform continuityIn mathematics, a function f is uniformly continuous if, roughly speaking, it is possible to guarantee that f and f be as close to each other as we please by requiring only that x and y are sufficiently close to each other; unlike ordinary continuity, the maximum distance between x and y cannot...
, uniform convergence, and Cauchy sequenceCauchy sequenceIn mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses...
s. - A Cauchy netCauchy netIn mathematics, a Cauchy net generalizes the notion of Cauchy sequence to nets defined on uniform spaces.A net is a Cauchy net if for every entourage V there exists γ such that for all α, β ≥ γ, is a member of V. More generally, in a Cauchy space, a net is Cauchy if the filter generated by the...
in a locally convex space is a netNet (mathematics)In mathematics, more specifically in general topology and related branches, a net or Moore–Smith sequence is a generalization of the notion of a sequence. In essence, a sequence is a function with domain the natural numbers, and in the context of topology, the range of this function is...
{xκ}κ such that for every ε > 0 and every seminorm pα, there exists a κ such that for every λ, μ > κ, pα(xλ–xμ) < ε. In other words, the net must be Cauchy in all the seminorms simultaneously. The definition of completeness is given here in terms of nets instead of the more familiar sequenceSequenceIn mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
s because unlike Fréchet spaces which are metrisable, general spaces may be defined by an uncountable family of pseudometrics. Sequences, which are countable by definition, cannot suffice to characterize convergence in such spaces. A locally convex space is complete if and only if every Cauchy net converges. - A family of seminorms becomes a preorderPreorderIn mathematics, especially in order theory, preorders are binary relations that are reflexive and transitive.For example, all partial orders and equivalence relations are preorders...
ed set under the relation pα ≤ pβ if and only if there exists an M > 0 such that for all x, pα(x) ≤ Mpβ(x). One says it is a directed family of seminorms if the family is a directed setDirected setIn mathematics, a directed set is a nonempty set A together with a reflexive and transitive binary relation ≤ , with the additional property that every pair of elements has an upper bound: In other words, for any a and b in A there must exist a c in A with a ≤ c and b ≤...
with addition as the join, in other words if for every α and β, there is a γ such that pα + pβ ≤ pγ. Every family of seminorms has an equivalent directed family, meaning one which defines the same topology. Indeed, given a family {pα}α∈I, let Φ be the set of finite subsets of I, then for every F in Φ, define qF=∑α∈F pα. One may check that {qF}F∈Φ is an equivalent directed family. - If the topology of the space is induced from a single seminorm, then the space is seminormable. Any locally convex space with a finite family of seminorms is seminormable. Moreover, if the space is Hausdorff (the family is separated), then the space is normable, with norm given by the sum of the seminorms. In terms of the open sets, a locally convex topological vector space is seminormable if and only if 0 has a boundedBounded set (topological vector space)In functional analysis and related areas of mathematics, a set in a topological vector space is called bounded or von Neumann bounded, if every neighborhood of the zero vector can be inflated to include the set...
neighborhood.
Examples of locally convex spaces
- Every normed space is a Hausdorff locally convex space, and much of the theory of locally convex spaces generalises parts of the theory of normed spaces. The family of seminorms can be taken to be the single norm. Every Banach space is a complete Hausdorff locally convex space, in particular, the Lp spacesLp spaceIn mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
with p ≥ 1 are locally convex.
- More generally, every Fréchet space is locally convex. A Fréchet space can be defined as a complete locally convex space with a separated countable family of seminorms.
- The space Rω of real valued sequences with the family of seminorms given by
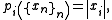i ∈ N. The countable family of seminorms is complete and separable, so this is a Fréchet space, which is not normable. Note that this is also the limit topology of the spaces Rn, embedded in Rω in the natural way, by completing finite sequences with infinitely many 0.
- Given any vector space V and a collection F of linear functionals on it, V can be made into a locally convex topological vector space by giving it the weakest topology making all linear functionals in F continuous. This is known as the weak topologyWeak topologyIn mathematics, weak topology is an alternative term for initial topology. The term is most commonly used for the initial topology of a topological vector space with respect to its continuous dual...
or the initial topologyInitial topologyIn general topology and related areas of mathematics, the initial topology on a set X, with respect to a family of functions on X, is the coarsest topology on X which makes those functions continuous.The subspace topology and product topology constructions are both special cases of initial...
determined by F. The collection F may be the algebraic dual of V or any other collection. The family of seminorms in this case is given by pƒ(x) = |ƒ(x)| for all ƒ in F.
- Spaces of differentiable functions give other non-normable examples. Consider the space of smooth functions ƒ : Rn → C such that supx |xaDbƒ| < ∞, where a and b are multiindices. The family of seminorms define by pa,b(ƒ) = supx |xaDbƒ(x)| is separated, and countable, and the space is complete, so this metrisable space is a Fréchet space. It is known as the Schwartz space, or the space of functions of rapid decrease, and its dual spaceDual spaceIn mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
is the space of tempered distributionTempered representationIn mathematics, a tempered representation of a linear semisimple Lie group is a representation that has a basis whose matrix coefficients lie in the Lp spacefor any ε > 0.-Formulation:...
s.
- An important function spaceFunction spaceIn mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
in functional analysis is the space D(U) of smooth functions with compact support in U ⊆ Rn. A more detailed construction is needed for the topology of this space because the space C∞0(U) is not complete in the uniform norm. The topology on D(U) is defined as follows: for any fixed compact set K ⊂ U, the space C∞0(K) of functions ƒ ∈ C∞0(U) with supp(ƒ) ⊂ K is a Fréchet spaceFréchet spaceIn functional analysis and related areas of mathematics, Fréchet spaces, named after Maurice Fréchet, are special topological vector spaces. They are generalizations of Banach spaces...
with countable family of seminorms ||ƒ||m = supx |Dmƒ(x)| (these are actually bona fide norms, and the space C∞0(K) with the ||·||m norm is a Banach space Dm(K)) . Given any collection {Kλ}λ of compact sets, directed by inclusion and such that ∪λKλ = U, then the C∞0(Kλ) form a direct system, and D(U) is defined to be the limit of this system. Such a limit of Fréchet spaces is known as an LF space. More concretely, D(U) is the union of all the C∞0(Kλ) with the final topologyFinal topologyIn general topology and related areas of mathematics, the final topology on a set X, with respect to a family of functions into X, is the finest topology on X which makes those functions continuous.- Definition :Given a set X and a family of topological spaces Y_i with functionsf_i: Y_i \to Xthe...
which makes each inclusion mapInclusion mapIn mathematics, if A is a subset of B, then the inclusion map is the function i that sends each element, x of A to x, treated as an element of B:i: A\rightarrow B, \qquad i=x....
C∞0(Kλ)↪D(U) continuous. This space is locally convex and sequentially complete, but not complete (this means that all Cauchy sequences converge, but not necessarily more general Cauchy nets). The space is not metrisable, and so it is not a Fréchet space. The dual space of D(Rn) is the space of distributionsDistribution (mathematics)In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
on Rn.
- More abstractly, given a topological spaceTopological spaceTopological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X, the space C(X) of continuous (not necessarily bounded) functions on X can be given the topology of uniform convergence on compact sets. This topology is defined by semi-norms φK(ƒ) = max { |ƒ(x)| : x ∈ K } (as K varies over the directed setDirected setIn mathematics, a directed set is a nonempty set A together with a reflexive and transitive binary relation ≤ , with the additional property that every pair of elements has an upper bound: In other words, for any a and b in A there must exist a c in A with a ≤ c and b ≤...
of all compact subsets of X). When X is locally compact (e.g. an open set in Rn) the Stone-Weierstrass theoremStone-Weierstrass theoremIn mathematical analysis, the Weierstrass approximation theorem states that every continuous function defined on an interval [a,b] can be uniformly approximated as closely as desired by a polynomial function...
applies -- in the case of real-valued functions, any subalgebra of C(X) that separates points and contains the constant functions (e.g., the subalgebra of polynomials) is denseDense setIn topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
.
Examples of spaces lacking local convexity
Many topological vector spaces are locally convex. Examples of spaces that lack local convexity include the following:- The spaces Lp([0, 1])Lp spaceIn mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
for 0 < p < 1 are equipped with the F-normF-spaceIn functional analysis, an F-space is a vector space V over the real or complex numbers together with a metric d : V × V → R so that...
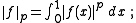
they are not locally convex, since the only convex neighborhood of zero is the whole space. More generally the spaces Lp(μ) with an atomless, finite measure μ and 0 < p < 1 are not locally convex.
- The space of measurable functions on the unit intervalUnit intervalIn mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
[0, 1] (where we identify two functions that are equal almost everywhereAlmost everywhereIn measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
) has a vector-space topology defined by the translation-invariant metric (which induces the convergence in measureConvergence in measureConvergence in measure can refer to two distinct mathematical concepts which both generalizethe concept of convergence in probability.-Definitions:...
of measurable functions; for random variables, convergence in measure is convergence in probability). This space is often denoted L0.
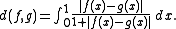
Both examples have the property that any continuous linear map to the real numbers is 0. In particular, their dual space
Dual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
is trivial, that is, it contains only the zero functional.
- The sequence space ℓp, 0 < p < 1, is not locally convex.
Continuous linear mappings
Because locally convex spaces are topological spaces as well as vector spaces, the natural functions to consider between two locally convex spaces are continuous linear maps. Using the seminorms, a necessary and sufficient criterion for the continuity of a linear map can be given that closely resembles the more familiar boundedness conditionBounded operator
In functional analysis, a branch of mathematics, a bounded linear operator is a linear transformation L between normed vector spaces X and Y for which the ratio of the norm of L to that of v is bounded by the same number, over all non-zero vectors v in X...
found for Banach spaces.
Given locally convex spaces V and W with families of seminorms {pα}α and {qβ}β respectively, a linear map T from V to W is continuous if and only if for every β there exist α1, α2, ... , αn and exists an M>0 such that for all x in X
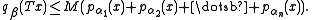
In other words, each seminorm of the range of T is bounded
Bounded function
In mathematics, a function f defined on some set X with real or complex values is called bounded, if the set of its values is bounded. In other words, there exists a real number M...
above by some finite sum of seminorms in the domain. If the family {pα}α is a directed family, and it can always be chosen to be directed as explained above, then the formula becomes even simpler and more familiar:
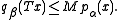
The class
Class (set theory)
In set theory and its applications throughout mathematics, a class is a collection of sets which can be unambiguously defined by a property that all its members share. The precise definition of "class" depends on foundational context...
of all locally convex topological vector spaces forms a category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
with continuous linear maps as morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
s.