Admissible representation
Encyclopedia
In mathematics, admissible representations are a well-behaved class of representations
used in the representation theory
of reductive
Lie group
s and locally compact
totally disconnected group
s. They were introduced by Harish-Chandra
.
V is called admissible if π restricted to K is unitary and each irreducible unitary representation of K occurs in it with finite multiplicity. The prototypical example is that of an irreducible unitary representation of G.
An admissible representation π induces a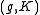
-module
which is easier to deal with as it is an algebraic object. Two admissible representations are said to be infinitesimally equivalent if their associated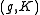
-modules are isomorphic. Though for general admissible representations, this notion is different than the usual equivalence, it is an important result that the two notions of equivalence agree for unitary (admissible) representations. Additionally, there is a notion of unitarity of 
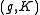-modules. This reduces the study of the equivalence classes of irreducible unitary representations of G to the study of infinitesimal equivalence classes of admissible representations and the determination of which of these classes are infinitesimally unitary. The problem of parameterizing the infinitesimal equivalence classes of admissible representations was fully solved by Robert Langlands
and is called the Langlands classification
.
or over the finite adeles
of a global field
). A representation (π, V) of G on a complex vector space V is called smooth if the subgroup of G fixing any vector of V is open
. If, in addition, the space of vectors fixed by any compact
open subgroup is finite dimensional then π is called admissible. Admissible representations of p-adic groups admit more algebraic description through the action of the Hecke algebra
of locally constant functions on G.
Deep studies of admissible representations of p-adic reductive groups were undertaken by Casselman and by Bernstein
and Zelevinsky in the 1970s. Much progress has been made more recently by Howe
and Moy and Bushnell and Kutzko, who developed a theory of types and classified the admissible dual (i.e. the set of equivalence classes of irreducible admissible representations) in many cases.
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
used in the representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
of reductive
Reductive group
In mathematics, a reductive group is an algebraic group G over an algebraically closed field such that the unipotent radical of G is trivial . Any semisimple algebraic group is reductive, as is any algebraic torus and any general linear group...
Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s and locally compact
Locally compact group
In mathematics, a locally compact group is a topological group G which is locally compact as a topological space. Locally compact groups are important because they have a natural measure called the Haar measure. This allows one to define integrals of functions on G.Many of the results of finite...
totally disconnected group
Totally disconnected group
In mathematics, a totally disconnected group is a topological group that is totally disconnected. Such topological groups are necessarily Hausdorff....
s. They were introduced by Harish-Chandra
Harish-Chandra
Harish-Chandra was an Indian mathematician, who did fundamental work in representation theory, especially Harmonic analysis on semisimple Lie groups. -Life:...
.
Real or complex reductive Lie groups
If G is a connected reductive (real or complex) Lie group and K is a maximal compact subgroup. A continuous representation (π, V) of G on a complex Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
V is called admissible if π restricted to K is unitary and each irreducible unitary representation of K occurs in it with finite multiplicity. The prototypical example is that of an irreducible unitary representation of G.
An admissible representation π induces a
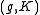-module(g,K)-module
In mathematics, more specifically in the representation theory of reductive Lie groups, a -module is an algebraic object, first introduced by Harish-Chandra, used to deal with continuous infinite-dimensional representations using algebraic techniques...
which is easier to deal with as it is an algebraic object. Two admissible representations are said to be infinitesimally equivalent if their associated
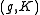-modules are isomorphic. Though for general admissible representations, this notion is different than the usual equivalence, it is an important result that the two notions of equivalence agree for unitary (admissible) representations. Additionally, there is a notion of unitarity of 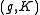-modules. This reduces the study of the equivalence classes of irreducible unitary representations of G to the study of infinitesimal equivalence classes of admissible representations and the determination of which of these classes are infinitesimally unitary. The problem of parameterizing the infinitesimal equivalence classes of admissible representations was fully solved by Robert LanglandsRobert Langlands
Robert Phelan Langlands is a mathematician, best known as the founder of the Langlands program. He is an emeritus professor at the Institute for Advanced Study...
and is called the Langlands classification
Langlands classification
In mathematics, the Langlands classification is a classification of irreducible representations of a reductive Lie group G, suggested by Robert Langlands...
.
Totally disconnected groups
Let G be a locally compact totally disconnected group (such as a reductive algebraic group over a local fieldLocal field
In mathematics, a local field is a special type of field that is a locally compact topological field with respect to a non-discrete topology.Given such a field, an absolute value can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean and...
or over the finite adeles
Adele ring
In algebraic number theory and topological algebra, the adele ring is a topological ring which is built on the field of rational numbers . It involves all the completions of the field....
of a global field
Global field
In mathematics, the term global field refers to either of the following:*an algebraic number field, i.e., a finite extension of Q, or*a global function field, i.e., the function field of an algebraic curve over a finite field, equivalently, a finite extension of Fq, the field of rational functions...
). A representation (π, V) of G on a complex vector space V is called smooth if the subgroup of G fixing any vector of V is open
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
. If, in addition, the space of vectors fixed by any compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
open subgroup is finite dimensional then π is called admissible. Admissible representations of p-adic groups admit more algebraic description through the action of the Hecke algebra
Hecke algebra of a locally compact group
In mathematics, a Hecke algebra of a locally compact group is an algebra of binvariant measures under convolution.Let be a pair consisting of a unimodular locally compact topological group G and a closed subgroup K of G...
of locally constant functions on G.
Deep studies of admissible representations of p-adic reductive groups were undertaken by Casselman and by Bernstein
Joseph Bernstein
Joseph Bernstein is an Israeli mathematician working at Tel Aviv University. He works in algebraic geometry, representation theory, and number theory....
and Zelevinsky in the 1970s. Much progress has been made more recently by Howe
Roger Evans Howe
Roger Evans Howe is the William R. Kenan Jr. Professor of Mathematics at Yale University. He is well known for his contributions to representation theory, and in particular for the notion of a reductive dual pair, sometimes known as a Howe pair, and the Howe correspondence.He attended Ithaca High...
and Moy and Bushnell and Kutzko, who developed a theory of types and classified the admissible dual (i.e. the set of equivalence classes of irreducible admissible representations) in many cases.