Restricted representation
Encyclopedia
In mathematics
, restriction is a fundamental construction in representation theory of group
s. Restriction forms a representation of a subgroup from a representation of the whole group. Often the restricted representation is simpler to understand. Rules for decomposing the restriction of an irreducible representation into irreducible representations of the subgroup are called branching rules, and have important applications in physics. For example, in case of explicit symmetry breaking
, the symmetry group of the problem is reduced from the whole group to one of its subgroup. In quantum mechanics
, this reduction in symmetry appears as a splitting of degenerate states into multiplets, as in the Stark
or Zeeman effect
.
The induced representation
is a related operation that forms a representation of the whole group from a representation of a subgroup. The relation between restriction and induction is described by Frobenius reciprocity and the Mackey theorem. Restriction to a normal subgroup
behaves particularly well and is often called Clifford theory
after the theorem of A. H. Clifford. Restriction can be generalized to other group homomorphism
s and to other rings
.
For any group G, its subgroup
H, and a linear representation ρ of G, the restriction of ρ to H, denoted
is a representation of H on the same vector space by the same operators:
G to a classical subgroup H, i.e. the multiplicity with which an irreducible representation (σ, W) of H occurs in π. By Frobenius reciprocity for compact group
s, this is equivalent to finding the multiplicity of π in the unitary representation induced from σ. Branching rules for the classical groups were determined by
between successive unitary group
s; between successive special orthogonal groups and unitary symplectic groups; from the unitary groups to the unitary symplectic groups and special orthogonal groups.
The results are usually expressed graphically using Young diagrams to encode the signatures used classically to label irreducible representations, familiar from classical invariant theory
. Hermann Weyl
and Richard Brauer
discovered a systematic method for determining the branching rule when the groups G and H share a common maximal torus
: in this case the Weyl group
of H is a subgroup of that of G, so that the rule can be deduced from the Weyl character formula
. A systematic modern interpretation has been given by in the context of his theory of dual pair
s. The special case where σ is the trivial representation of H was first used extensively by Hua in his work on the Szegő kernels of bounded symmetric domain
s in several complex variables
, where the Shilov boundary
has the form G/H. More generally the Cartan-Helgason theorem gives the decomposition when G/H is a compact symmetric space, in which case all multiplicities are one; a generalization to arbitrary σ has since been obtained by . Similar geometric considerations have also been used by to rederive Littlewood's rules, which involve the celebrated Littlewood-Richardson rules for tensoring irreducible representations of the unitary groups.
has found generalizations of these rules to arbitrary compact semisimple Lie groups, using his path model
, an approach to representation theory close in spirit to the theory of crystal bases of Lusztig and Kashiwara. His methods yield branching rules for restrictions to subgroups containing a maximal torus
. The study of branching rules is important in classical invariant theory and its modern counterpart, algebraic combinatorics
.
Example. The unitary group U(N) has irreducible representations labelled by signatures
where the fi are integers. In fact if a unitary matrix U has eigenvalues zi, then the character of the corresponding irreducible representation πf is given by
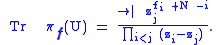
The branching rule from U(N) to U(N – 1) states that
Example. The unitary symplectic group or quaternionic unitary group, denoted Sp(N) or U(N, H), is the group of all transformations of
HN which commute with right multiplication by the quaternions H and preserve the H-valued hermitian inner product
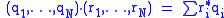
on HN, where q* denotes the quaternion conjugate to q. Realizing quaternions as 2 x 2 complex matrices,
the group Sp(N) is just the group of block matrices
(qij) in SU(2N) with
where αij and βij are complex number
s.
Each matrix U in Sp(N) is conjugate to a block diagonal matrix with entries
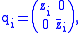
where |zi| = 1. Thus the eigenvalues of U are (zi±1). The irreducible representations of Sp(N)
are labelled by signatures
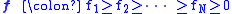
where the fi are integers. The character of the corresponding irreducible representation σf is given by
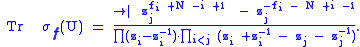
The branching rule from Sp(N) to Sp(N – 1) states that
Here fN + 1 = 0 and the multiplicity
m(f, g) is given by
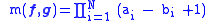
where
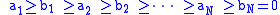
is the non-increasing rearrangement of the 2N non-negative integers (fi), (gj) and 0.
Example. The branching from U(2N) to Sp(N) relies on two identities of Littlewood
:
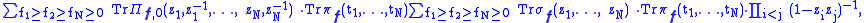
where Πf,0 is the irreducible representation of U(2N) with signature f1 ≥ ··· ≥ fN ≥ 0 ≥ ··· ≥ 0.
where fi ≥ 0.
The branching rule from U(2N) to Sp(N) is given by
where all the signature are non-negative and the coefficient M (g, h; k) is the multiplicity of the irreducible representation πk of U(N) in the tensor product πg
πh. It is given combinatorially by the Littlewood-Richardson rule, the number of lattice permutations of the skew diagram k/h of weight g.
There is an extension of Littelwood's branching rule to arbitrary signatures due to . The Littlewood-Richardson coefficients M (g, h; f) are extended to allow the signature f to have 2N parts but restricting g to have
even column-lengths (g2i – 1 = g2i). In this case the formula reads
where MN (g, h; f) counts the number of lattice permutations of f/h of weight g are counted for which 2j + 1 appears no lower than row N + j of f for 1 ≤ j ≤ |g|/2.
Example. The special orthogonal group SO(N) has irreducible ordinary and spin representations labelled by signatures
The fi are taken in Z for ordinary representations and in ½ + Z for spin representations. In fact if an orthogonal matrix U has eigenvalues zi±1 for 1 ≤ i ≤ n, then the character of the corresponding irreducible representation πf is given by
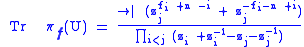
for N = 2n and by
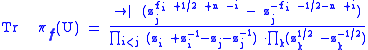
for N = 2n+1.
The branching rules from SO(N) to SO(N – 1) state that
\pi_{\mathbf{g}}
|}
for N = 2n+1 and
\pi_{\mathbf{g}}
|}
for N = 2n, where the differences fi - gi must be integers.
smaller and smaller N will eventually terminate in one dimensional subspaces. In this way Gelfand and Tsetlin were able to obtain a basis of any irreducible representation of U(N) or SO(N) labelled by a chain of interleaved signatures, called a Gelfand-Tsetlin pattern.
Explicit formulas for the action of the Lie algebra on the Gelfand-Tsetlin basis are given in .
For the remaining classical group Sp(N), the branching is no longer multiplicity free, so that if V and W are irreducible representation of Sp(N–1) and
Sp(N) the space of intertwiners HomSp(N–1)(V,W) can have dimension greater than one. It turns out that the Yangian
Y(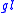
2), a Hopf algebra
introduced by Ludwig Faddeev and collaborators
, acts irreducibly on this multiplicity space, a fact which enabled to extend the construction of Gelfand-Tsetlin bases to Sp(N).
proved the following result on the restriction of finite-dimensional irreducible representations from a group G to a normal subgroup
N of finite index
:
Theorem. Let π: G
GL(n,K) be an irreducible representation with K a field
. Then
the restriction of π to N breaks up into a direct sum of inequivalent irreducible representations of N of equal dimensions. These irreducible representations of N lie in one orbit for the action of G by conjugation on the equivalence classes of irreducible representations of N. In particular the number of distinct summands is no greater than the index of N in G.
Twenty years later George Mackey
found a more precise version of this result for the restriction of irreducible unitary representation
s of locally compact group
s to closed normal subgroups in what has become known as the "Mackey machine" or "Mackey normal subgroup analysis".
, restriction is an instance of a forgetful functor
. This functor is exact, and its left adjoint functor is called induction
. The relation between restriction and induction in various contexts is called the Frobenius reciprocity. Taken together, the operations of induction and restriction form a powerful set of tools for analyzing representations. This is especially true whenever the representations have the property of complete reducibility, for example, in representation theory of finite groups
over a field of characteristic zero.
φ from H to G, instead of the inclusion map
, and define the restricted representation of H by the composition
We may also apply the idea to other categories in abstract algebra
: associative algebra
s, ring
s, Lie algebra
s, Lie superalgebra
s, Hopf algebra
s to name some. Representations or module
s restrict to subobjects, or via homomorphisms.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, restriction is a fundamental construction in representation theory of group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
s. Restriction forms a representation of a subgroup from a representation of the whole group. Often the restricted representation is simpler to understand. Rules for decomposing the restriction of an irreducible representation into irreducible representations of the subgroup are called branching rules, and have important applications in physics. For example, in case of explicit symmetry breaking
Explicit symmetry breaking
Explicit symmetry breaking indicates a situation where the dynamical equations are not manifestly invariant under the symmetry group considered. This means, in the Lagrangian formulation, that the Lagrangian of the system contains one or more terms explicitly breaking the symmetry...
, the symmetry group of the problem is reduced from the whole group to one of its subgroup. In quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, this reduction in symmetry appears as a splitting of degenerate states into multiplets, as in the Stark
Stark effect
The Stark effect is the shifting and splitting of spectral lines of atoms and molecules due to presence of an external static electric field. The amount of splitting and or shifting is called the Stark splitting or Stark shift. In general one distinguishes first- and second-order Stark effects...
or Zeeman effect
Zeeman effect
The Zeeman effect is the splitting of a spectral line into several components in the presence of a static magnetic field. It is analogous to the Stark effect, the splitting of a spectral line into several components in the presence of an electric field...
.
The induced representation
Induced representation
In mathematics, and in particular group representation theory, the induced representation is one of the major general operations for passing from a representation of a subgroup H to a representation of the group G itself. It was initially defined as a construction by Frobenius, for linear...
is a related operation that forms a representation of the whole group from a representation of a subgroup. The relation between restriction and induction is described by Frobenius reciprocity and the Mackey theorem. Restriction to a normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
behaves particularly well and is often called Clifford theory
Clifford theory
In mathematics, Clifford theory, introduced by , describes the relation between representations of a group and those of a normal subgroup.Alfred H. Clifford proved the following result on the restriction of finite-dimensional irreducible representations from a group G to a normal subgroup N of...
after the theorem of A. H. Clifford. Restriction can be generalized to other group homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
s and to other rings
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
.
For any group G, its subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
H, and a linear representation ρ of G, the restriction of ρ to H, denoted
- ρ|H,
is a representation of H on the same vector space by the same operators:
- ρ|H(h) = ρ(h).
Classical branching rules
Classical branching rules describe the restriction of an irreducible representation (π, V) of a classical groupClassical group
In mathematics, the classical Lie groups are four infinite families of Lie groups closely related to the symmetries of Euclidean spaces. Their finite analogues are the classical groups of Lie type...
G to a classical subgroup H, i.e. the multiplicity with which an irreducible representation (σ, W) of H occurs in π. By Frobenius reciprocity for compact group
Compact group
In mathematics, a compact group is a topological group whose topology is compact. Compact groups are a natural generalisation of finite groups with the discrete topology and have properties that carry over in significant fashion...
s, this is equivalent to finding the multiplicity of π in the unitary representation induced from σ. Branching rules for the classical groups were determined by
between successive unitary group
Unitary group
In mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
s; between successive special orthogonal groups and unitary symplectic groups; from the unitary groups to the unitary symplectic groups and special orthogonal groups.
The results are usually expressed graphically using Young diagrams to encode the signatures used classically to label irreducible representations, familiar from classical invariant theory
Invariant theory
Invariant theory is a branch of abstract algebra dealing with actions of groups on algebraic varieties from the point of view of their effect on functions...
. Hermann Weyl
Hermann Weyl
Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
and Richard Brauer
Richard Brauer
Richard Dagobert Brauer was a leading German and American mathematician. He worked mainly in abstract algebra, but made important contributions to number theory...
discovered a systematic method for determining the branching rule when the groups G and H share a common maximal torus
Maximal torus
In the mathematical theory of compact Lie groups a special role is played by torus subgroups, in particular by the maximal torus subgroups.A torus in a Lie group G is a compact, connected, abelian Lie subgroup of G . A maximal torus is one which is maximal among such subgroups...
: in this case the Weyl group
Weyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
of H is a subgroup of that of G, so that the rule can be deduced from the Weyl character formula
Weyl character formula
In mathematics, the Weyl character formula in representation theory describes the characters of irreducible representations of compact Lie groups in terms of their highest weights. It was proved by ....
. A systematic modern interpretation has been given by in the context of his theory of dual pair
Reductive dual pair
In the mathematical field of representation theory, a reductive dual pair is a pair of subgroups of the isometry group Sp of a symplectic vector space W, such that G is the centralizer of G ′ in Sp and vice versa, and these groups act reductively on W...
s. The special case where σ is the trivial representation of H was first used extensively by Hua in his work on the Szegő kernels of bounded symmetric domain
Hermitian symmetric space
In mathematics, a Hermitian symmetric space is a Kähler manifold M which, as a Riemannian manifold, is a Riemannian symmetric space. Equivalently, M is a Riemannian symmetric space with a parallel complex structure with respect to which the Riemannian metric is Hermitian...
s in several complex variables
Several complex variables
The theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
, where the Shilov boundary
Shilov boundary
In functional analysis, a branch of mathematics, the Shilov boundary is the smallest closed subset of the structure space of a commutative Banach algebra where an analog of the maximum modulus principle holds...
has the form G/H. More generally the Cartan-Helgason theorem gives the decomposition when G/H is a compact symmetric space, in which case all multiplicities are one; a generalization to arbitrary σ has since been obtained by . Similar geometric considerations have also been used by to rederive Littlewood's rules, which involve the celebrated Littlewood-Richardson rules for tensoring irreducible representations of the unitary groups.
has found generalizations of these rules to arbitrary compact semisimple Lie groups, using his path model
Littelmann path model
In mathematics, the Littelmann path model is a combinatorial device due to Peter Littelmann for computing multiplicities without overcounting in the representation theory of symmetrisable Kac-Moody algebras. Its most important application is to complex semisimple Lie algebras or equivalently...
, an approach to representation theory close in spirit to the theory of crystal bases of Lusztig and Kashiwara. His methods yield branching rules for restrictions to subgroups containing a maximal torus
Maximal torus
In the mathematical theory of compact Lie groups a special role is played by torus subgroups, in particular by the maximal torus subgroups.A torus in a Lie group G is a compact, connected, abelian Lie subgroup of G . A maximal torus is one which is maximal among such subgroups...
. The study of branching rules is important in classical invariant theory and its modern counterpart, algebraic combinatorics
Algebraic combinatorics
Algebraic combinatorics is an area of mathematics that employs methods of abstract algebra, notably group theory and representation theory, in various combinatorial contexts and, conversely, applies combinatorial techniques to problems in algebra....
.
Example. The unitary group U(N) has irreducible representations labelled by signatures
where the fi are integers. In fact if a unitary matrix U has eigenvalues zi, then the character of the corresponding irreducible representation πf is given by
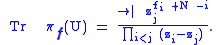
The branching rule from U(N) to U(N – 1) states that
Example. The unitary symplectic group or quaternionic unitary group, denoted Sp(N) or U(N, H), is the group of all transformations of
HN which commute with right multiplication by the quaternions H and preserve the H-valued hermitian inner product
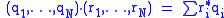
on HN, where q* denotes the quaternion conjugate to q. Realizing quaternions as 2 x 2 complex matrices,
the group Sp(N) is just the group of block matrices
Block matrix
In the mathematical discipline of matrix theory, a block matrix or a partitioned matrix is a matrix broken into sections called blocks. Looking at it another way, the matrix is written in terms of smaller matrices. We group the rows and columns into adjacent 'bunches'. A partition is the rectangle...
(qij) in SU(2N) with
where αij and βij are complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s.
Each matrix U in Sp(N) is conjugate to a block diagonal matrix with entries
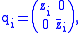
where |zi| = 1. Thus the eigenvalues of U are (zi±1). The irreducible representations of Sp(N)
are labelled by signatures
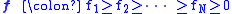
where the fi are integers. The character of the corresponding irreducible representation σf is given by
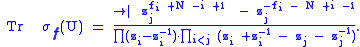
The branching rule from Sp(N) to Sp(N – 1) states that
Here fN + 1 = 0 and the multiplicity
Multiplicity (mathematics)
In mathematics, the multiplicity of a member of a multiset is the number of times it appears in the multiset. For example, the number of times a given polynomial equation has a root at a given point....
m(f, g) is given by
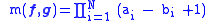
where
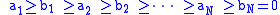
is the non-increasing rearrangement of the 2N non-negative integers (fi), (gj) and 0.
Example. The branching from U(2N) to Sp(N) relies on two identities of Littlewood
Dudley E. Littlewood
Dudley Ernest Littlewood was a British mathematician known for his work in group representation theory....
:
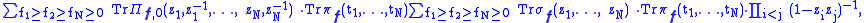
where Πf,0 is the irreducible representation of U(2N) with signature f1 ≥ ··· ≥ fN ≥ 0 ≥ ··· ≥ 0.
where fi ≥ 0.
The branching rule from U(2N) to Sp(N) is given by
where all the signature are non-negative and the coefficient M (g, h; k) is the multiplicity of the irreducible representation πk of U(N) in the tensor product πg
πh. It is given combinatorially by the Littlewood-Richardson rule, the number of lattice permutations of the skew diagram k/h of weight g.There is an extension of Littelwood's branching rule to arbitrary signatures due to . The Littlewood-Richardson coefficients M (g, h; f) are extended to allow the signature f to have 2N parts but restricting g to have
even column-lengths (g2i – 1 = g2i). In this case the formula reads
where MN (g, h; f) counts the number of lattice permutations of f/h of weight g are counted for which 2j + 1 appears no lower than row N + j of f for 1 ≤ j ≤ |g|/2.
Example. The special orthogonal group SO(N) has irreducible ordinary and spin representations labelled by signatures
-
for N = 2n; 
for N = 2n+1.
The fi are taken in Z for ordinary representations and in ½ + Z for spin representations. In fact if an orthogonal matrix U has eigenvalues zi±1 for 1 ≤ i ≤ n, then the character of the corresponding irreducible representation πf is given by
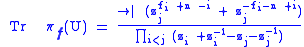
for N = 2n and by
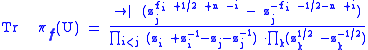
for N = 2n+1.
The branching rules from SO(N) to SO(N – 1) state that
|}
for N = 2n+1 and
|}
for N = 2n, where the differences fi - gi must be integers.
Gelfand-Tsetlin basis
Since the branching rules from U(N) to U(N–1) or SO(N) to SO(N–1) have multiplicity one, the irreducible summands corresponding tosmaller and smaller N will eventually terminate in one dimensional subspaces. In this way Gelfand and Tsetlin were able to obtain a basis of any irreducible representation of U(N) or SO(N) labelled by a chain of interleaved signatures, called a Gelfand-Tsetlin pattern.
Explicit formulas for the action of the Lie algebra on the Gelfand-Tsetlin basis are given in .
For the remaining classical group Sp(N), the branching is no longer multiplicity free, so that if V and W are irreducible representation of Sp(N–1) and
Sp(N) the space of intertwiners HomSp(N–1)(V,W) can have dimension greater than one. It turns out that the Yangian
Yangian
Yangian is an important structure in modern representation theory, a type of a quantum group with origins in physics. Yangians first appeared in the work of Ludvig Faddeev and his school concerning the quantum inverse scattering method in the late 1970s and early 1980s. Initially they were...
Y(
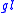2), a Hopf algebraHopf algebra
In mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property.Hopf algebras occur naturally...
introduced by Ludwig Faddeev and collaborators
Lomi
Lomi or Pancit Lomi is a Filipino-Chinese dish made with a variety of thick fresh egg noodles of about a quarter of an inch in diameter. Because of its popularity at least in the eastern part of Batangas, there are as many styles of cooking lomi as there are eateries, panciterias or restaurants...
, acts irreducibly on this multiplicity space, a fact which enabled to extend the construction of Gelfand-Tsetlin bases to Sp(N).
Clifford's theorem
In 1937 Alfred H. CliffordAlfred H. Clifford
Alfred Hoblitzelle Clifford was an American mathematician who is known for Clifford theory and for his work on semigroups. The Alfred H. CliffordMathematics Research Library at Tulane University is named after him....
proved the following result on the restriction of finite-dimensional irreducible representations from a group G to a normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
N of finite index
Index of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
:
Theorem. Let π: G
GL(n,K) be an irreducible representation with K a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
. Then
the restriction of π to N breaks up into a direct sum of inequivalent irreducible representations of N of equal dimensions. These irreducible representations of N lie in one orbit for the action of G by conjugation on the equivalence classes of irreducible representations of N. In particular the number of distinct summands is no greater than the index of N in G.
Twenty years later George Mackey
George Mackey
George Whitelaw Mackey was an American mathematician. Mackey earned his bachelor of arts at Rice University in 1938 and obtained his Ph.D. at Harvard University in 1942 under the direction of Marshall H. Stone...
found a more precise version of this result for the restriction of irreducible unitary representation
Unitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
s of locally compact group
Locally compact group
In mathematics, a locally compact group is a topological group G which is locally compact as a topological space. Locally compact groups are important because they have a natural measure called the Haar measure. This allows one to define integrals of functions on G.Many of the results of finite...
s to closed normal subgroups in what has become known as the "Mackey machine" or "Mackey normal subgroup analysis".
Abstract algebraic setting
From the point of view of category theoryCategory theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, restriction is an instance of a forgetful functor
Forgetful functor
In mathematics, in the area of category theory, a forgetful functor is a type of functor. The nomenclature is suggestive of such a functor's behaviour: given some object with structure as input, some or all of the object's structure or properties is 'forgotten' in the output...
. This functor is exact, and its left adjoint functor is called induction
Induced representation
In mathematics, and in particular group representation theory, the induced representation is one of the major general operations for passing from a representation of a subgroup H to a representation of the group G itself. It was initially defined as a construction by Frobenius, for linear...
. The relation between restriction and induction in various contexts is called the Frobenius reciprocity. Taken together, the operations of induction and restriction form a powerful set of tools for analyzing representations. This is especially true whenever the representations have the property of complete reducibility, for example, in representation theory of finite groups
Representation theory of finite groups
In mathematics, representation theory is a technique for analyzing abstract groups in terms of groups of linear transformations. See the article on group representations for an introduction...
over a field of characteristic zero.
Generalizations
This rather evident construction may be extended in numerous and significant ways. For instance we may take any group homomorphismGroup homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
φ from H to G, instead of the inclusion map
Inclusion map
In mathematics, if A is a subset of B, then the inclusion map is the function i that sends each element, x of A to x, treated as an element of B:i: A\rightarrow B, \qquad i=x....
, and define the restricted representation of H by the composition
- ρoφ.
We may also apply the idea to other categories in abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
: associative algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
s, ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
s, Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
s, Lie superalgebra
Lie superalgebra
In mathematics, a Lie superalgebra is a generalisation of a Lie algebra to include a Z2-grading. Lie superalgebras are important in theoretical physics where they are used to describe the mathematics of supersymmetry...
s, Hopf algebra
Hopf algebra
In mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property.Hopf algebras occur naturally...
s to name some. Representations or module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
s restrict to subobjects, or via homomorphisms.