
Tensor product of algebras
Encyclopedia
In mathematics
, the tensor product
of two R-algebras
is also an R-algebra. This gives us a tensor product of algebras. The special case R = Z gives us a tensor product of rings, since rings may be regarded as Z-algebras.
Let R be a commutative ring
and let A and B be R-algebras
. Since A and B may both be regarded as R-modules
, we may form their tensor product
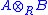
which is also an R-module. We can give the tensor product the structure of an algebra by defining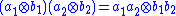
and then extending by linearity to all of A⊗RB. This product is easily seen to be R-bilinear, associative, and unital with an identity element given by 1A⊗1B, where 1A and 1B are the identities of A and B. If A and B are both commutative then the tensor product is as well.
The tensor product turns the category
of all R-algebras into a symmetric monoidal category.
There are natural homomorphisms of A and B to A⊗RB given by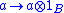

These maps make the tensor product a coproduct
in the category of commutative R-algebras. (The tensor product is not the coproduct in the category of all R-algebras. There the coproduct is given by a more general free product
of algebras).
The tensor product of algebras is of constant use in algebraic geometry
: working in the opposite category
to that of commutative R-algebras, it provides pullback
s of affine schemes, otherwise known as fiber products.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
of two R-algebras
Algebra (ring theory)
In mathematics, specifically in ring theory, an algebra over a commutative ring is a generalization of the concept of an algebra over a field, where the base field K is replaced by a commutative ring R....
is also an R-algebra. This gives us a tensor product of algebras. The special case R = Z gives us a tensor product of rings, since rings may be regarded as Z-algebras.
Let R be a commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
and let A and B be R-algebras
Algebra (ring theory)
In mathematics, specifically in ring theory, an algebra over a commutative ring is a generalization of the concept of an algebra over a field, where the base field K is replaced by a commutative ring R....
. Since A and B may both be regarded as R-modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
, we may form their tensor product
Tensor product of modules
In mathematics, the tensor product of modules is a construction that allows arguments about bilinear maps to be carried out in terms of linear maps...
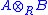
which is also an R-module. We can give the tensor product the structure of an algebra by defining
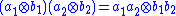
and then extending by linearity to all of A⊗RB. This product is easily seen to be R-bilinear, associative, and unital with an identity element given by 1A⊗1B, where 1A and 1B are the identities of A and B. If A and B are both commutative then the tensor product is as well.
The tensor product turns the category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of all R-algebras into a symmetric monoidal category.
There are natural homomorphisms of A and B to A⊗RB given by
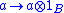

These maps make the tensor product a coproduct
Coproduct
In category theory, the coproduct, or categorical sum, is the category-theoretic construction which includes the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the...
in the category of commutative R-algebras. (The tensor product is not the coproduct in the category of all R-algebras. There the coproduct is given by a more general free product
Free product
In mathematics, specifically group theory, the free product is an operation that takes two groups G and H and constructs a new group G ∗ H. The result contains both G and H as subgroups, is generated by the elements of these subgroups, and is the “most general” group having these properties...
of algebras).
The tensor product of algebras is of constant use in algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
: working in the opposite category
Opposite category
In category theory, a branch of mathematics, the opposite category or dual category Cop of a given category C is formed by reversing the morphisms, i.e. interchanging the source and target of each morphism. Doing the reversal twice yields the original category, so the opposite of an opposite...
to that of commutative R-algebras, it provides pullback
Pullback (category theory)
In category theory, a branch of mathematics, a pullback is the limit of a diagram consisting of two morphisms f : X → Z and g : Y → Z with a common codomain; it is the limit of the cospan X \rightarrow Z \leftarrow Y...
s of affine schemes, otherwise known as fiber products.

