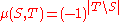Incidence algebra
Encyclopedia
In order theory
, a field of mathematics
, an incidence algebra is an associative algebra
, defined for any locally finite partially ordered set
and commutative ring
with unity.
within it is finite.
The members of the incidence algebra are the function
s f assigning to each nonempty interval [a, b] a scalar f(a, b), which is taken from the ring of scalars
, a commutative ring
with unity. On this underlying set one defines addition and scalar multiplication pointwise, and "multiplication" in the incidence algebra is a convolution
defined by
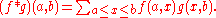
An incidence algebra is finite-dimensional if and only if the underlying poset is finite.
; indeed, both the group algebra and the incidence algebra are special cases of a categorical algebra
, defined analogously; groups
and posets
being special kinds of categories
.
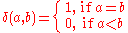
The zeta function of an incidence algebra is the constant function ζ(a, b) = 1 for every interval [a, b]. Multiplying by ζ is analogous to integration.
One can show that ζ is invertible in the incidence algebra (with respect to the convolution defined above). (Generally, a member h of the incidence algebra is invertible if and only if h(x, x) is invertible for every x.) The multiplicative inverse of the zeta function is the Möbius function μ(a, b); every value of μ(a, b) is an integral multiple of 1 in the base ring.
The Möbius function can also be defined directly, by the following relation: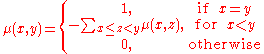
Multiplying by μ is analogous to differentiation, and is called Möbius inversion.
Order theory
Order theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
, a field of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an incidence algebra is an associative algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
, defined for any locally finite partially ordered set
and commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
with unity.
Definition
A locally finite poset is one for which every closed intervalInterval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
- [a, b] = {x : a ≤ x ≤ b}
within it is finite.
The members of the incidence algebra are the function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s f assigning to each nonempty interval [a, b] a scalar f(a, b), which is taken from the ring of scalars
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
, a commutative ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
with unity. On this underlying set one defines addition and scalar multiplication pointwise, and "multiplication" in the incidence algebra is a convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
defined by
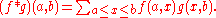
An incidence algebra is finite-dimensional if and only if the underlying poset is finite.
Related concepts
An incidence algebra is analogous to a group algebraGroup ring
In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
; indeed, both the group algebra and the incidence algebra are special cases of a categorical algebra
Categorical algebra
In category theory, a field of mathematics, a categorical algebra is an associative algebra, defined for any locally finite category and commutative ring with unity.It generalizes the notions of group algebra and incidence algebra,...
, defined analogously; groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
and posets
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
being special kinds of categories
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
.
Special elements
The multiplicative identity element of the incidence algebra is the delta function, defined by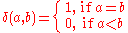
The zeta function of an incidence algebra is the constant function ζ(a, b) = 1 for every interval [a, b]. Multiplying by ζ is analogous to integration.
One can show that ζ is invertible in the incidence algebra (with respect to the convolution defined above). (Generally, a member h of the incidence algebra is invertible if and only if h(x, x) is invertible for every x.) The multiplicative inverse of the zeta function is the Möbius function μ(a, b); every value of μ(a, b) is an integral multiple of 1 in the base ring.
The Möbius function can also be defined directly, by the following relation:
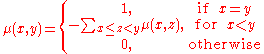
Multiplying by μ is analogous to differentiation, and is called Möbius inversion.
Examples
- Positive integers ordered by divisibility
- The Möbius function is μ(a, b) = μ(b/a), where the second "μ" is the classical Möbius functionMöbius functionThe classical Möbius function μ is an important multiplicative function in number theory and combinatorics. The German mathematician August Ferdinand Möbius introduced it in 1832...
introduced into number theory in the 19th century.
- Finite subsetSubsetIn mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of some set E, ordered by inclusion
- The Möbius function is
- whenever S and T are finite subsets of E with S ⊆ T, and Möbius inversion is called the principle of inclusion-exclusion.
- Geometrically, this is a hypercubeHypercubeIn geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
:
- Natural numbers with their usual order
- The Möbius function is
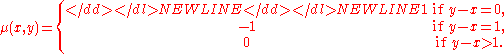
- and Möbius inversion is called the (backwards) difference operator.
- Geometrically, this corresponds to the discrete number lineNumber lineIn basic mathematics, a number line is a picture of a straight line on which every point is assumed to correspond to a real number and every real number to a point. Often the integers are shown as specially-marked points evenly spaced on the line...
. - Recall that convolution of sequences corresponds to multiplication of formal power seriesFormal power seriesIn mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
.
- The Möbius function corresponds to the sequence (1, −1, 0, 0, 0, ... ) of coefficients of the formal power series 1 − z, and the zeta function in this case corresponds to the sequence of coefficients (1, 1, 1, 1, ... ) of the formal power series
 , which is inverse. The delta function in this incidence algebra similarly corresponds to the formal power series 1.
, which is inverse. The delta function in this incidence algebra similarly corresponds to the formal power series 1.
- Subgroups of a finite p-group G, ordered by inclusion
- The Möbius function is
 if
if 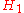 is a normal subgroup of
is a normal subgroup of 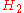 and
and 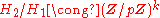
- and it is 0 otherwise. This is a theorem of Weisner (1935).
- Finite sub-multisets of some multisetMultisetIn mathematics, the notion of multiset is a generalization of the notion of set in which members are allowed to appear more than once...
E, ordered by inclusion
- The above three examples can be unified and generalized by considering a multiset E, and finite sub-multisets S and T of E. The Möbius function is
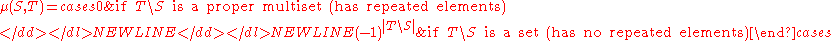
- This generalizes the positive integers ordered by divisibility by a positive integer corresponding to its multiset of prime divisors with multiplicity, e.g., 12 corresponds to the multiset

- This generalizes the natural numbers with their usual order by a natural number corresponding to a multiset of one underlying element and cardinality equal to that number, e.g., 3 corresponds to the multiset
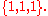
- Partitions of a set
- Partially order the set of all partitionsPartition of a setIn mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
of a finite set by saying σ ≤ τ if σ is a finer partition than τ. Then the Möbius function is
- where n is the number of blocks in the finer partition σ, r is the number of blocks in the coarser partition τ, and ri is the number of blocks of τ that contain exactly i blocks of σ.
Euler characteristic
A poset is bounded if it has smallest and largest elements, which we call 0 and 1 respectively (not to be confused with the 0 and 1 of the ring of scalars). The Euler characteristic of a bounded finite poset is μ(0,1); it is always an integer. This concept is related to the classical Euler characteristicEuler characteristicIn mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
.
Reduced incidence algebras
Any member of an incidence algebra that assigns the same value to any two intervals that are isomorphic to each other as posets is a member of the reduced incidence algebra. This is a subalgebra of the incidence algebra, and it clearly contains the incidence algebra's identity element and zeta function. Any element of the reduced incidence algebra that is invertible in the larger incidence algebra has its inverse in the reduced incidence algebra. As a consequence, the Möbius function is always a member of the reduced incidence algebra. Reduced incidence algebras shed light on the theory of generating functionGenerating functionIn mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
s, as alluded to in the case of the natural numbers above.
Literature
Incidence algebras of locally finite posets were treated in a number of papers of Gian-Carlo RotaGian-Carlo RotaGian-Carlo Rota was an Italian-born American mathematician and philosopher.-Life:Rota was born in Vigevano, Italy...
beginning in 1964, and by many later combinatorialistsCombinatoricsCombinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
. Rota's 1964 paper was:
- N. Jacobson, Basic Algebra. I, W. H. Freeman and Co., 1974. See section 8.6 for a treatment of Mobius functions on posets
- This generalizes the positive integers ordered by divisibility by a positive integer corresponding to its multiset of prime divisors with multiplicity, e.g., 12 corresponds to the multiset