
Free product
Encyclopedia
In mathematics
, specifically group theory
, the free product is an operation that takes two groups
G and H and constructs a new group G ∗ H. The result contains both G and H as subgroup
s, is generated
by the elements of these subgroups, and is the “most general” group having these properties. Unless one of the groups G and H is trivial, the free product is always infinite. The construction of a free product is similar in spirit to the construction of a free group
(the most general group that can be made from a given set of generators).
The free product is the coproduct
in the category of groups
. That is, the free product plays the same role in group theory that disjoint union
plays in set theory
, or that the direct sum
plays in module theory.
The free product is important in algebraic topology
because of van Kampen's theorem, which states that the fundamental group
of the union
of two path-connected
topological space
s is always an amalgamated free product of the fundamental groups of the spaces. In particular, the fundamental group of the wedge sum
of two spaces (i.e. the space obtained by joining two spaces together at a single point) is simply the free product of the fundamental groups of the spaces.
Free products are also important in Bass–Serre theory
, the study of groups acting
by automorphisms on trees
. Specifically, any group acting with finite vertex stabilizers on a tree may be constructed from finite groups using amalgamated free products and HNN extension
s. Using the action of the modular group
on a certain tessellation
of the hyperbolic plane
, it follows from this theory that the modular group is isomorphic to the free product of cyclic group
s of orders 4 and 6 amalgamated over a cyclic group of order 2.

where each si is either an element of G or an element of H. Such a word may be reduced using the following operations:
Every reduced word is an alternating product of elements of G and elements of H, e.g.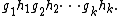
The free product G ∗ H is the group whose elements are the reduced words in G and H, under the operation of concatenation followed by reduction.
For example, if G is the infinite cyclic group <x>, and H is the infinite cyclic group <y>, then every element of G ∗ H is an alternating product of powers of x with powers of y. In this case, G ∗ H is isomorphic to the free group generated by x and y.

is a presentation
for G (where RG is a set of generators and SG is a set of relations), and suppose that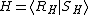
is a presentation for H. Then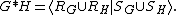
That is, G ∗ H is generated by the generators for G together with the generators for H, with relations consisting of the relations from G together with the relations from H (assume here no notational clashes so that these are in fact disjoint union
s).
For example, suppose that G is a cyclic group of order 4,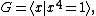
and H is a cyclic group of order 5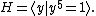
Then G ∗ H is the infinite group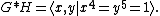
Because there are no relations in a free group, the free product of free groups is always a free group. In particular,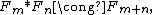
where Fn denotes the free group on n generators.
in the same category
. Suppose G and H are given as before, along with group homomorphism
s
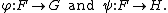
where F is some arbitrary group. Start with the free product G*H and adjoin as relations

for every f in F. In other words take the smallest normal subgroup
N of G ∗ H containing all elements on the left-hand side of the above equation, which are tacitly being considered in G ∗ H by means of the inclusions of G and H in their free product. The free product with amalgamation of G and H, with respect to φ and ψ, is the quotient group
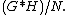
The amalgamation has forced an identification between φ(F) in G with ψ(F) in H, element by element. This is the construction needed to compute the fundamental group of two connected spaces joined along a connected subspace, with F taking the role of the fundamental group of the subspace. See: Seifert–van Kampen theorem
.
Free products with amalgamation and a closely related notion of HNN extension
are basic building blocks in Bass–Serre theory of groups acting on trees.
. Free products of algebras of random variable
s play the same role in defining "freeness
" in the theory of free probability
that Cartesian product
s play in defining statistical independence
in classical probability theory
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, the free product is an operation that takes two groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
G and H and constructs a new group G ∗ H. The result contains both G and H as subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s, is generated
Generating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
by the elements of these subgroups, and is the “most general” group having these properties. Unless one of the groups G and H is trivial, the free product is always infinite. The construction of a free product is similar in spirit to the construction of a free group
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
(the most general group that can be made from a given set of generators).
The free product is the coproduct
Coproduct
In category theory, the coproduct, or categorical sum, is the category-theoretic construction which includes the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the...
in the category of groups
Category of groups
In mathematics, the category Grp has the class of all groups for objects and group homomorphisms for morphisms. As such, it is a concrete category...
. That is, the free product plays the same role in group theory that disjoint union
Disjoint union
In mathematics, the term disjoint union may refer to one of two different concepts:* In set theory, a disjoint union is a modified union operation that indexes the elements according to which set they originated in; disjoint sets have no element in common.* In probability theory , a disjoint union...
plays in set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, or that the direct sum
Direct sum of modules
In abstract algebra, the direct sum is a construction which combines several modules into a new, larger module. The result of the direct summation of modules is the "smallest general" module which contains the given modules as submodules...
plays in module theory.
The free product is important in algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
because of van Kampen's theorem, which states that the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of the union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of two path-connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s is always an amalgamated free product of the fundamental groups of the spaces. In particular, the fundamental group of the wedge sum
Wedge sum
In topology, the wedge sum is a "one-point union" of a family of topological spaces. Specifically, if X and Y are pointed spaces the wedge sum of X and Y is the quotient of the disjoint union of X and Y by the identification x0 ∼ y0:X\vee Y = \;/ \sim,\,where ∼ is the...
of two spaces (i.e. the space obtained by joining two spaces together at a single point) is simply the free product of the fundamental groups of the spaces.
Free products are also important in Bass–Serre theory
Bass–Serre theory
Bass–Serre theory is a part of the mathematical subject of group theory that deals with analyzing the algebraic structure of groups acting by automorphisms on simplicial trees...
, the study of groups acting
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
by automorphisms on trees
Tree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
. Specifically, any group acting with finite vertex stabilizers on a tree may be constructed from finite groups using amalgamated free products and HNN extension
HNN extension
In mathematics, the HNN extension is a basic construction of combinatorial group theory.Introduced in a 1949 paper Embedding Theorems for Groups by Graham Higman, B. H...
s. Using the action of the modular group
Modular group
In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
on a certain tessellation
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
of the hyperbolic plane
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
, it follows from this theory that the modular group is isomorphic to the free product of cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
s of orders 4 and 6 amalgamated over a cyclic group of order 2.
Construction
If G and H are groups, a word in G and H is a product of the form
where each si is either an element of G or an element of H. Such a word may be reduced using the following operations:
- Remove an instance of the identity element (of either G or H).
- Replace a pair of the form g1g2 by its product in G, or a pair h1h2 by its product in H.
Every reduced word is an alternating product of elements of G and elements of H, e.g.
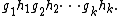
The free product G ∗ H is the group whose elements are the reduced words in G and H, under the operation of concatenation followed by reduction.
For example, if G is the infinite cyclic group <x>, and H is the infinite cyclic group <y>, then every element of G ∗ H is an alternating product of powers of x with powers of y. In this case, G ∗ H is isomorphic to the free group generated by x and y.
Presentation
Suppose that
is a presentation
Presentation of a group
In mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...
for G (where RG is a set of generators and SG is a set of relations), and suppose that
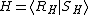
is a presentation for H. Then
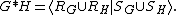
That is, G ∗ H is generated by the generators for G together with the generators for H, with relations consisting of the relations from G together with the relations from H (assume here no notational clashes so that these are in fact disjoint union
Disjoint union
In mathematics, the term disjoint union may refer to one of two different concepts:* In set theory, a disjoint union is a modified union operation that indexes the elements according to which set they originated in; disjoint sets have no element in common.* In probability theory , a disjoint union...
s).
For example, suppose that G is a cyclic group of order 4,
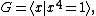
and H is a cyclic group of order 5
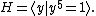
Then G ∗ H is the infinite group
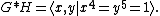
Because there are no relations in a free group, the free product of free groups is always a free group. In particular,
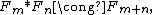
where Fn denotes the free group on n generators.
Generalization: Free product with amalgamation
The more general construction of free product with amalgamation is correspondingly a pushoutPushout (category theory)
In category theory, a branch of mathematics, a pushout is the colimit of a diagram consisting of two morphisms f : Z → X and g : Z → Y with a common domain: it is the colimit of the span X \leftarrow Z \rightarrow Y.The pushout is the...
in the same category
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
. Suppose G and H are given as before, along with group homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
s
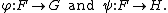
where F is some arbitrary group. Start with the free product G*H and adjoin as relations

for every f in F. In other words take the smallest normal subgroup
Conjugate closure
In group theory, the conjugate closure of a subset S of a group G is the subgroup of G generated by SG, i.e. the closure of SG under the group operation, where SG is the conjugates of the elements of S:The conjugate closure of S is denoted or G.The conjugate closure of any subset S of a group G...
N of G ∗ H containing all elements on the left-hand side of the above equation, which are tacitly being considered in G ∗ H by means of the inclusions of G and H in their free product. The free product with amalgamation of G and H, with respect to φ and ψ, is the quotient group
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
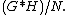
The amalgamation has forced an identification between φ(F) in G with ψ(F) in H, element by element. This is the construction needed to compute the fundamental group of two connected spaces joined along a connected subspace, with F taking the role of the fundamental group of the subspace. See: Seifert–van Kampen theorem
Seifert–van Kampen theorem
In mathematics, the Seifert-van Kampen theorem of algebraic topology, sometimes just called van Kampen's theorem, expresses the structure of the fundamental group of a topological space X, in terms of the fundamental groups of two open, path-connected subspaces U and V that cover X...
.
Free products with amalgamation and a closely related notion of HNN extension
HNN extension
In mathematics, the HNN extension is a basic construction of combinatorial group theory.Introduced in a 1949 paper Embedding Theorems for Groups by Graham Higman, B. H...
are basic building blocks in Bass–Serre theory of groups acting on trees.
In other branches
One may similarly define free products of other algebraic structures than groups, including algebras over a fieldAlgebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
. Free products of algebras of random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s play the same role in defining "freeness
Free independence
In the mathematical theory of free probability, the notion of free independence was introduced by Dan Voiculescu. The definition of free independence is parallel to the classical definition of independence, except that the role of Cartesian products of measure spaces is played by the notion of a...
" in the theory of free probability
Free probability
Free probability is a mathematical theory that studies non-commutative random variables. The "freeness" or free independence property is the analogue of the classical notion of independence, and it is connected with free products....
that Cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
s play in defining statistical independence
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
in classical probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
.
See also
- Direct product of groupsDirect product of groupsIn the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...
- Free objectFree objectIn mathematics, the idea of a free object is one of the basic concepts of abstract algebra. It is a part of universal algebra, in the sense that it relates to all types of algebraic structure . It also has a formulation in terms of category theory, although this is in yet more abstract terms....
- Graph of groupsGraph of groupsIn geometric group theory, a graph of groups is an object consisting of a collection of groups indexed by the vertices and edges of a graph, together with a family of monomorphisms of the edge groups into the vertex groups....
- Kurosh subgroup theoremKurosh subgroup theoremIn the mathematical field of group theory, the Kurosh subgroup theorem describes the algebraic structure of subgroups of free products of groups. The theorem was obtained by Alexander Kurosh, a Russian mathematician, in 1934...
- Universal propertyUniversal propertyIn various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...

